【本讲教育信息】

一. 教学内容：

第四节 电势能、电势

第五节 电势差

二. 知识要点：

1. 理解静电力做功的特点、电势能的概念、电势能与电场力做功的关系。

2. 理解电势的概念，知道电势是描述电场的能的性质的物理量。明确电势能、电势、静电力的功、电势能的关系。了解电势与电场线的关系，了解等势面的意义及与电场线的关系。理解掌握电势差的概念、定义式与应用。

三. 重点、难点解析：

1. 静电力做功的特点

试探电荷q在场强为E的均强电场中沿不同路径从A运动到B电场力做功的情况。

（1）q沿直线从A到B

（2）q沿折线从A到M、再从M到B

（3）q沿任意曲线A到B

结果都一样即：W=qEL_AM =qEL_ABcos

结论：在任何电场中，静电力移动电荷所做的功，只与始末两点的位置有关，而与电荷的运动路径无关。

2. 电势能

（1）电势能：由于移动电荷时静电力做功与移动的路径无关，电荷在电场中也具有势能，这种势能叫做电势能。

（2）静电力做功与电势能变化的关系：

静电力做的功等于电势能的变化量。写成式子为：

注意：

① 电场力做正功，电荷的电势能减小；电场力做负功，电荷的电势能增加

② 电场力做多少功，电势能就变化多少，在只受电场力作用下，电势能与动能相互转化，而它们的总量保持不变。

③ 在正电荷产生的电场中正电荷在任意一点具有的电势能都为正，负电荷在任

一点具有的电势能都为负。

在负电荷产生的电场中正电荷在任意一点具有的电势能都为负，负电荷在任意一点具有的电势能都为正。

④ 求电荷在电场中某点具有的电势能

电荷在电场中某一点A具有的电势能E_P等于将该点电荷由A点移到电势零点电场力所做的功W，即E_P=W

⑤ 求电荷在电场中A、B两点具有的电势能高低

将电荷由A点移到B点根据电场力做功情况判断，电场力做正功，电势能减小，电荷在A点电势能大于在B点的电势能，反之电场力做负功，电势能增加，电荷在A点的电势能小于在B点的电势能。

⑥ 电势能零点的规定

若要确定电荷在电场中的电势能，应先规定电场中电势能的零位置。

关于电势能零点的规定：大地或无穷远默认为零。

所以：电荷在电场中某点的电势能，等于静电力把它从该点移动到零电势能位置时电场力所有做的功。如上式若取B为电势能零点，则A点的电势能为：

3. 电势——表征电场性质的重要物理量度

通过研究电荷在电场中电势能与它的电荷量的比值得出。参阅P₂₀图1.4—3

（1）定义：电荷在电场中某一点的电势能与它的电荷量的比值，叫做这一点的电势。用表示。标量，只有大小，没有方向，但有正负。

（2）公式：（与试探电荷无关）

（3）单位：伏特（V）

（4）电势与电场线的关系：电势顺线降低。（电场线指向电势降低的方向）

（5）零电势位置的规定：电场中某一点的电势的数值与零电势的选择有关，即电势的数值决定于零电势的选择。（大地或无穷远默认为零）

4. 电势差

定义：电荷在电场中由一点A移动到另一点B，电场力所做的功W_AB与电量的比值叫做AB两点间的电势差。即U_AB=。

说明：（1）定义U_AB=中，W_AB可为正值，也可为负值，q为电荷所带电量，正电荷取正值，负电荷取负值。

（2） 电场中两点的电势差只与两点位置有关，与在这两点间移动电荷的电量、电场力做功的大小无关。在确定的电场中，既便不放入电荷，任何两点间的电势差都有确定的值，不能认为U_AB与W_AB成正比，与q成反比。只是可以利用W_AB、q来测量A、B两点电势差U_AB

（3）公式W=qU适用任何电场

① 由比值定义式U_AB=W_AB／q可以看出，U_AB在数值上等于单位正电荷由A移到B点时电场力所做的功W_AB若电场对单位正电荷做正功，U_AB为正值；若电场对单位正电荷做负功，则U_AB为负值。

② 讲到电势差时，必须明确所指的是哪两点（两位置）的电势差。A、B间的电势差记作U_AB。一电荷q在电场中由A到B做的功W_AB与从B到A做的功W_BA存在关系：W_AB=－W_BA 所以U_AB=－U_BA电势差有正负，通过后面的学习，同学们将知道，电势差的正负仅表示电场中两点电势的高低，如U_AB=6V，说明A点的电势比B点的电势高6V。

5. 等势面

（1）定义：电场中电势相等的点构成的面

（2）等势面的性质：

① 在同一等势面上各点电势相等，所以在同一等势面上移动电荷，电场力不做功

② 电场线跟等势面一定垂直，并且由电势高的等势面指向电势低的等势面。

③ 等势面越密，电场强度越大

④ 等势面不相交，不相切

（3）等势面的用途：由等势面描绘电场线，判断电场中电势的高低。

（4）几种电场的电场线及等势面

① 点电荷电场中的等势面：以点电荷为球心的一簇球面如图l所示。

② 等量异种点电荷电场中的等势面：是两簇对称曲面，如图2所示。

③ 等量同种点电荷电场中的等势面：是两簇对称曲面，如图3所示。

④ 匀强电场中的等势面是垂直于电场线的一簇平面，如图4所示。

⑤ 形状不规则的带电导体附近的电场线及等势面，如图5所示。

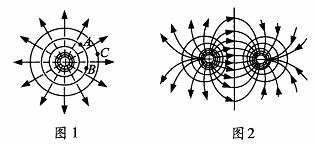
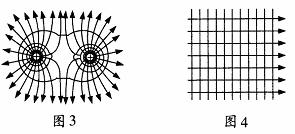
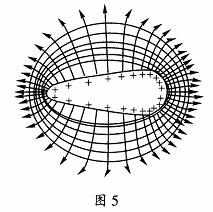
注意：带方向的线表示电场线，无方向的线表示等势面。图中的等势“面”画成了线，即以“线”代“面”。

6. 比较电荷在电场中某两点电势能大小的方法

（1）做功判断法

无论正、负电荷，电场力做正功，电荷从电势能较大的地方移向电势能较小的地方，反之，如果电荷克服电场力做功，那么电荷将从电势能较小的地方移向电势能较大的地方。

（2）电场线法

正电荷顺着电场线的方向移动时，电势能逐渐减小；逆着电场线的方向移动时，电势能逐渐增大。

负电荷顺着电场线的方向移动时，电势能逐渐增大；逆着电场线的方向移动时，电势能逐渐减小

（3）由公式E_P=qφ判断

设φ_A>φ_B，当q>0时，qφ_A>qφ_B，即E_pB>E_pA 当q<0时，qφ_A<qφ_B即E_PA<E_PB，可总结为正电荷在电势高的地方电势能大，而负电荷在电势高的地方电势能小。

【典型例题】

[例1] 下列说法中正确的是（ ）

A. 无论是正电荷还是负电荷，从电场中某点移到无穷远处时，电场力做的正功越多，电荷在该点的电势能就越大

B. 无论是正电荷还是负电荷，从电场中某点移到无穷远处时，电场力做的正功越少，电荷在该点的电势能越大

C. 无论是正电荷还是负电荷，从无穷远处移到电场中某点时，克服电场力做功越多，电荷在该点的电势能越大

D. 无论是正电荷还是负电荷，从无穷远处移到电场中某点时，电场力做功越多，电荷在该点的电势能越大

解析：无穷远处的电势能为零，电荷从电场中某处移到无穷远时，若电场力做正功，电势能减少，到无穷远处时电势能减为零，电荷在该点的电势能为正值，且等于移动过程中电荷电势能的变化，也就等于电场力做的功，因此电场力做的正功越多，电荷在该点电势能越大，A正确，B错误。电荷从无穷远处移到电场中某点时，若克服电场力做功，电势能由零增大到某值，此值就是电荷在该点的电势能值，因此，电荷在该点的电势能等于电荷从无穷远处移到该点时，克服电场力所做的功，故C正确，D错误。

答案：A、C

[例2] 一个带正电的质点，电量q=2 0×l0^-9c，在静电场中由a点移到b点，在这个过程中，除电场力外，其他力做功6 0×10^-5J，质点的动能增加了8.0×l0^-5J，则a，b两点的电势差φ_a－φ_b为（ ）

A. 3×l0⁴V B. 1×10⁴V C. 4×l0⁴V D. 7×10⁴V

解析：由动能定理，外力对物体做功的代数和等于物体动能的增量，得电场力对物体做的功W=8.0×l0^-5J－6 0×l0^-5J=2.0×l0^-5 J。由W=q（φ_a－φ_b）得

φ_a－φ_b==1.0×10⁴V

答案：B

[例3] 如图所示，匀强电场电场线与AC平行，把l0^-8C的负电荷从A点移到B点，电场力做功6×l0^-5J，AB长6cm，AB与AC成60º角。求：

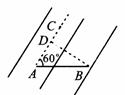
（1）场强方向；

（2）设B处电势为lV，则A处电势为多少?

（3）场强为多少?电子在A点电势能为多少?

解析：（1）将负电荷从A移至B，电场力做正功，所以所受电场力方向沿A至C。又因为是负电荷，场强方向与负电荷受力方向相反，所以场强方向应为C至A方向。

（2）由W=qU，得U_AB=== －6V

且U_AB=φ_A－φ_B= －6V，故φ_A=1V－6V= －5V，即A点的电势为－5V。

（3）由B向AC作垂线交AC于D，D与B在同一等势面上。

U_DA=U_BA=U=6V，沿场强方向AD两点距离为AB·cos60º=0.06×（1／2）m=0.03 m，所以，场强

E=U／d=6V／0.03 m=200（V／m）

电子在A点的电势能ε=qU=（－e）×（－5V）=5eV

[例4] 如图所示，虚线a、b、c表示电场中的三个等势面与纸平面的交线，且相邻等势面之间的电势差相等。实线为一带正电粒子仅在电场力作用下通过该区域时的运动轨迹，M、N是这条轨迹上的两点，则下面说法中正确的是（ ）

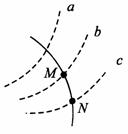
A. 三个等势面中，a的电势最高

B. 对于M、N两点，带电粒子通过N点时电势能较大

C. 对于M、N两点，带电粒子通过M点时动能较大

D. 带电粒子由M运动到N时，加速度增大

解析：由于带电粒子做曲线运动，所受电场力的方向必定指向轨道的凹侧，且和等势面垂直，所以电场线方向是由c指向b再指向a。根据电场线的方向是指电势降低的方向，故U_c>U_b>U_a，选项A错。

带正电粒子若从N点运动到M点，场强方向与运动方向成锐角，电场力做正功，即电势能减少；若从M点运动到N点。场强方向与运动方向成钝角，电场力做负功，电势能增加，故选项B对。

根据能量守恒定律，电荷的动能和电势能之和不变，故粒子在M点的动能较大，选项C正确。

由于相邻等势面之间电势差相等，因N点等势面较密，则E_N>E_M，即qE_N>qE_M。由牛顿第二定律知，带电粒子从M点运动到N点时，加速度增大，选项D正确，所以正确答案为B、C、D项。

[例5] 如图所示，实线为电场线，虚线为等势面，相邻两等势面间的电势差相等。一个正电荷在等势面L₃处的动能为20 J，运动到等势面L₁处时动能为零；现取L₂为零电势参考平面，则当此电荷的电势能为4 J时，它的动能为（不计重力及空气阻力）（ ）

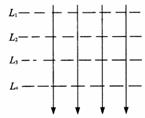
A. 16 J B. 10 J C. 6 J D. 4 J

解析：正电荷在电场中只受电场力的作用，在L₃时，动能为20 J，运动到L₂等势面时其动能一定是10 J。此时电势能为零，则此正电荷动能和电势能总和为10 J。当它的电势能为4 J时，动能一定为6 J。正确答案为C项。

【模拟试题】

1. 关于摩擦起电中做功及能量转化问题的解释，下列说法正确的是（ ）

A. 摩擦起电过程中，电场力做功

B. 摩擦起电过程中，电荷克服电场力做功

C. 摩擦起电过程中，其他形式的能转化为电势能

D. 摩擦起电过程中，电势能转化为其他形式的能

2. 如图所示，点电荷的静电场中电场线用实线表示，但其，方向未标明，虚线是某一带电粒子通过该电场区域时的运动轨迹。a、b是轨迹上的两点。若带电粒子在运动中只受到电场力作用，根据此图可作出正确判断的是（ ）

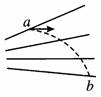
A. 带电粒子所带电荷的性质

B. 带电粒子在a、b两点的受力方向

C. 带电粒子在a、b两点的速度何处较大

D. 带电粒子在a、b两点的电势能何处较大

3. 如图所示，在场强为E的匀强电场中有相距为L的A、B两点，连线AB与电场线的夹角为θ，将一电荷量为q的正电荷从A点移到B点，若沿直线AB移动该电荷，电场力做的功W₁= ；若沿路径ACB移动该电荷，电场力做的功W₂= ；若沿曲线ADB移动该电荷，电场力做功W₃= 。由此可知电荷在电场中移动时，电场力做功的特点是

4. 带同种电荷的A、B球，质量分别为m和2m，开始均静止在光滑的绝缘水平面上。现将两个小球由静止同时释放，时刻t，A球的速率为v；从释放到时刻t，A、B两球的电势能改变量为

5. 关于电势差与电场力做功的说法中，正确的是（ ）

A. 电势差的大小由电场力在两点间移动电荷做的功和电荷的电量决定

B. 电场力在两点间移动电荷做功的多少由两点间的电势差和该电荷的电量决定

C. 电势差是矢量，电场力做的功是标量

D. 电场中两点间的电势差等于电场力做功后，电荷的电势能减小

6. 图是一匀强电场，已知场强E=2×10²N／C。现让一个电量q= －4×10^-8C的电荷沿电场方向从M点移到N点，MN间的距离s=30cm。试求：

（1）电荷从M点移到N点电势能的变化。

（2）M、N两点间的电势差。

7. 如图所示，电子在一条电场线上从a点运动到b点，电势能增加，试判定a、b两点电势高低。

8. 在图中，a，b带等量异种电荷，为ab连线的中垂线，现有一个带电粒子从M点以一定初速度v₀射出，开始时一段轨迹如图中实线，不考虑粒子重力，则在飞越该电场的整个过程中（ ）

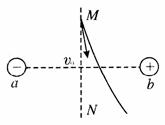
A. 该粒子带负电

B. 该粒子的动能先增大后减小

C. 该粒子的电势能先减小后增大

D. 该粒子运动到无穷远处后，速度的大小一定仍为v₀

9. 闪电是云层与云层或云层与地面上的高大建筑物之间的强烈放电现象。1970年春季的一个雷雨交加的天气，上午9时许，湖北古城黄州的青云塔顶被雷电击为两截。据有关专家估算，这次雷击所释放的能量至少有3.2×10⁶J。试求：

（1）在塔与云层之间放电过程中，电场力做功情况如何?在雷击现象中能量是怎样变化的?

（2）设从云层移向塔顶的电荷量为48C，试估算云层与塔顶之间的电压为多大?（取两位有效数字）

10. 如图所示，光滑绝缘细杆竖直放置，它与以正电荷Q为圆心的某圆交于B、C两点，质量为m、带电荷量－q的有孔小球从杆上A点无初速度下滑，已知qQ，AB=h，小球滑到B点时的速度大小为求：

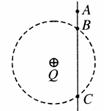
（1）小球由A到B的过程中电场力做的功；

（2）A、C两点的电势差

【试题答案】

1. BC 2. BCD

3. qELcosθ；qELcosθ；qELcosθ；电场力做功的大小与路径无关，只与始末位置有关

4. －

解析：由静止释放后，两球在库仑力作用下向相反方向运动，电场力做正功，电势能减少，电势能转化为两个小球的动能。

A、B两个带电小球组成的系统在水平方向上不受外力作用，动量守恒。当A球的速率为v时，它的动量值为mv；这时B球的动量值也是mv，B球的速率应为；时刻t，A球的动能为，B球的动能为（2m）·（）²=，它们的动能之和E_k=。

可见，电势能的改变量应为－。“－”号表示电势能减少

5. B

解析：电势差的大小由电场本身的因素决定，与移动电荷的电量及移动电荷所做的功无关，A项错。由W_AB=qU_AB知，B项对，电势差、电场力做的功都是标量，C项错。电场中两点的电势差等于单位电荷从一点移到另一点电场力所做的功，D项错。因此正确答案为B项。

6. 解析：（1）由图可知，负电荷在该电场中所受电场力F方向向左。因此从M点移到N点，电荷克服电场力做功，电势能增加，增加的电势能△E等于电荷克服电场力做的功W

电荷克服电场力做功为

W=qEs=4×10^-8×2×l0²×0.3J=2.4×10^-6J

即电荷从M点移到N点电势能增加了2.4×l0^-6J

（2）从M点到N点电场力对电荷做负功为W_MN= －2.4×l0^-6J，则MN两点间的电势差为

U_MN===60V

即M、N两点间的电势差为60V

7. 解析：解法一：

由于电势能增加，电场力一定做负功，即电场力方向和电荷运动方向相反，从b指向a而负电荷受电场力的方向和场强方向相反，场强方向应是由a指向b，因此电场线的方向是从a指向b。

顺着电场线的方向电势越来越低，a点电势比b点电势高

解法二：

由于电势能增加，电场力一定做负功，即W_ab为负值，而q是负电荷，即q为负值。

由W_ab=q（φ_a－φ_b）得知φ_a－φ_b>0，故φ_a>φ_b。

解法三：

正电荷q为正值，在电势越高的地方电势能越大，而对负电荷q为负值，在电势越高的地方电势能越小，而本题已知条件是负电荷在a点电势能较小，a点电势高

由于电势能增加，电场力一定做负功，即W_ab为负值，而q是负电荷，即q为负值

由Wab=q（φ_a－φ_b）得知φ_a－φ_b>0，故φ_a>φ_b

8. A、B、C、D

解析：等量异种电荷连线的中垂线一定是等势线，且与无穷远处等电势，这是本题考查的重点。至于粒子的动能增减、电势能变化情况，可以根据粒子轨迹的弯曲情况结合功能关系判断出来由粒子开始时一段轨迹可以判定，粒子在该电场中受到大致向右的电场力。因而可以判断粒子带负电，A正确。

因为等量异种电荷连线的中垂面是一个势面，又由两个电荷的电性可以判断。由a到b电势逐渐升高。即逆着电场线，也就是沿着电场力移动，所以电场力做正功，粒子电势能减小，动能增加。

但因为M点所处的等量异种电荷连线的中垂面与无穷远等电势，所以在由M点到无穷远运动的过程中，电场力做的总功为零，所以粒子到达无穷远处时动能仍然为原来值，即速度大小一定仍为v₀，D正确，因此电势能先减小后增大，动能先增大后减小，B、C正确。

9. （1）正功 （2）6.67×10⁵J

10. 解析：因为Q是点电荷，所以以Q为圆心的圆面是一个等势面，这是一个重要的隐含条件。由A到B过程中电场力是变力，所以不能直接用W=Fs来解，只能考虑应用功能关系

（1）因为杆是光滑的，所以小球从A到B过程中只有两个力做功：电场力的功W_AB和重力的功mgh，由动能定理得：

W_AB+mgh=，

代入已知条件v_B=得电场力做功

W_AB=－mgh=

（2）因为B、C在同一个等势面上

所以φ_B=φc，即U_AB=U_AC

由 W_AB=qU_AB

得 U_AB=U_AC= = －

故A、C两点电势差为一