课程信息

【本讲教育信息】

一. 教学内容：

    第九章  轴对称复习

 

［主要内容］

  1. 轴对称图形和轴对称的概念，以及两个概念之间的区别和联系。

  2. 简单的轴对称图形，如线段、角、正多边形、等腰三角形等。

  3. 等腰三角形的性质和识别。

 

［学习目标］

  1. 通过具体实例认识轴对称图形和轴对称的概念。

  2. 了解线段和角的轴对称特点及其性质。

  3. 通过画轴对称图形的对称轴，理解对应点所连结线段被对称轴垂直平分的性质。

  4. 能够按要求画出简单平面图形经过一次轴对称后的图形。

  5. 了解等腰三角形的概念，并掌握等腰三角形的性质。

  6. 掌握等腰三角形的识别方法。

  7. 了解等边三角形的概念，并掌握其性质及识别方法。

 

【典型例题】

  例1. 观察下列图形，哪些是轴对称图形，并指出他们各有几条对称轴？

    解：如果一个图形沿着某条直线对折，对折的两部分能够完全重合，那么这个图形就是轴对称图形。因此题中的图形是轴对称图形的有：（1），（2），（3），（5），（6），（7），（8），（9），（10），（11），（12），（13），（14），（19），（20），他们对称轴的条数分别为1，6，1，1，1，4，2，1，1，1，1，1，4，1，1。

 

  例2. 如下图所示，哪几个选项的右边的图形与左边的图形形成轴对称？

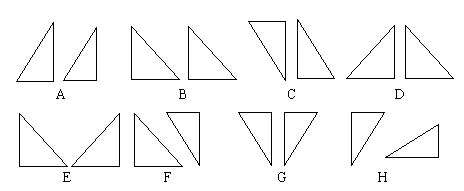
    解：两个图形成轴对称是指把一个图形沿着某条直线翻折过去能够与另一个图形完全重合，因此符合题意的选项有：D、E、G。

 

  例3. 如图，作出△ABC关于直线的轴对称图形。

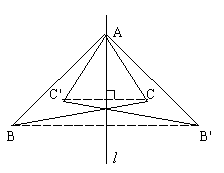
    解：因为A在对称轴上，因此A点关于的对称点就是它本身。我们只需作出B、C的对称点即可，分别作出B、C关于直线的对称点B'、C'，连结AB'、AC'、B'C'，△AB'C'就是△ABC关于直线的对称图形。

 

  例4. 已知：如图△ABC中，AB＝AC，AB的垂直平分线DE交AC于E，若BC＝a，△BEC的周长为b，求△ABC的周长。

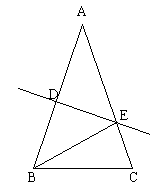
    分析：要求△ABC的周长，只需求AC或AB，而DE为线段AB的中垂线，所以BE＝AE，故可知，又由△BEC的周长为b，故。

    解：∵DE是线段AB的垂直平分线

   

    又∵△BEC的周长为b

   

    即

    又

   

    ∴△ABC的周长

                  

    即△ABC的周长为：

 

  例5. 如图，在△ABC中，∠C＝90°，BD平分∠ABC交AC于点D，AB的垂直平分线分别交AC、AB于点D、E，那么：

    （1）DE＝CD，为什么？

    （2）AD＝BD，为什么？

    （3）如果DE＝1cm，BD＝2cm，求AC的长。

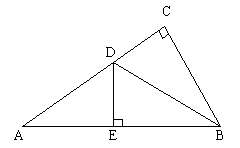
    解：（1）因为BD平分∠BAC，∠C＝90°，则DC⊥BC，又因DE⊥AB，根据角平分线上的点到这个角的两边的距离相等，所以DE＝DC。

    （2）因为DE是线段AB的垂直平分线，根据线段垂直平分线上的点到线段两端点的距离相等，所以AD＝BD。

    （3）∵CD＝DE＝1cm，AD＝BD＝2cm

   

 

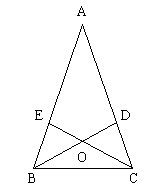
  例6. 如图，△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC，CE平分∠ACB，CE与BD交于点O，指出图中所有的等腰三角形。

    分析：识别等腰三角形关键是寻找该三角形是否有两边相等或两个内角相等，一般用到三角形内角和与外角知识及等腰三角形性质与角平分线、平行线等性质。

    解：∵AB＝AC

   

    ∵BD、CE平分∠ABC、∠ACB

   

    ∴△ABD、△ACE、△OBC是等腰三角形

    又

       

   

    ∴△BOE、△COD、△BCE、△BCD是等腰三角形

    ∴图中等腰三角形共有8个，分别是：△ABC、△ABD、△ACE、△OBC、△BOE、△COD、△BCE、△BCD

 

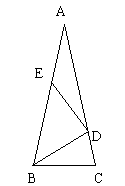
  例7. 已知：如图，在△ABC中，AB＝AC，点D、E分别在AC、AB上，且BC＝BD＝DE＝EA，求∠A的度数。

    解：∵DE＝AE

    ∴∠A＝∠ADE

    又∵DE＝BD

    ∴∠DEB＝∠DBE

    设∠A＝∠ADE＝x°

    ∵∠DEB是△AED的一个外角

   

    又∵∠BDC是△ABD的一个外角

   

    又∵BC＝BD

   

    又∵AB＝AC

   

    在△ABC中，∠A＋∠ABC＋∠C＝180°

   

 

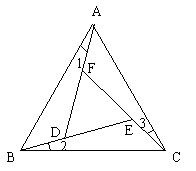
  例8. 如图，△ABC为等边三角形，且∠1＝∠2＝∠3。

    （1）求∠BEC的度数。

    （2）△DEF为等边三角形吗？请说明理由。

    解：（1）∵△ABC为等边三角形

    ∴∠BAC＝∠ABC＝∠ACB＝60°

    又∵∠2＝∠3

   

    在△BEC中，

   

    （2）从上面可知：∠BEC＝120°

   

    同理，∠DFE＝60°，∠FDE＝60°

   

    ∴△DEF为等边三角形

 

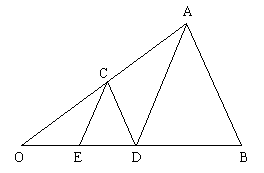
  例9. 如图，△AOB中，点C在OA上，点E、D在OB上，且CD∥AB，CE∥AD，AD＝AB，试说明△CDE是等腰三角形。

    解：∵AD＝AB

    ∴∠ADB＝∠ABD

    又∵CD∥AB

    ∴∠CDE＝∠ABD

    又∵CE∥AD

    ∴∠CED＝∠ADB

    ∴∠CDE＝∠CED

    ∴CE＝CD

    ∴△CDE是等腰三角形

 

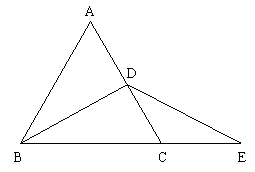
  例10. 如图，在等边△ABC中，D是AC的中点，延长BC到点E，使CE＝CD，AB＝10cm。

    （1）求BE的长；

    （2）BD＝ED吗？为什么？

    解：（1）∵△ABC是等边三角形

    ∴AB＝AC＝BC＝10cm

    又∵D是AC的中点

   

    又∵CD＝CE

    ∴CE＝5cm

   

    （2）BD＝ED。理由如下：

    ∵△ABC是等边三角形，D是AC的中点

    ∴∠ABC＝∠ACB＝60°

   

    又∵CD＝CE

    ∴∠CDE＝∠CED

    又∵∠ACB＝∠CDE＋∠CED

   

 

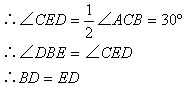
【模拟试题】（答题时间：45分钟）

一. 选择题。

  1. 下列图案是几种名车的标志，请你指出，在这几个图案中是轴对称图形的共有（    ）

    A. 4个           B. 3个           C. 2个           D. 1个

  2. “羊”字象征着美好和吉祥，下列图案都与“羊”字有关，其中是轴对称图形的个数是（    ）

    A. 1               B. 2               C. 3               D. 4

  3. 下列图形中，不是轴对称图形的是（    ）

    A. 有两个内角相等的三角形

    B. 三个内角度数比为3：4：5的三角形

    C. 有一个内角为45°的直角三角形

    D. 有两个内角分别为30°、120°的三角形

  4. 如果说一个等腰三角形的一个底角为α，那么（    ）

    A. 0°＜α＜90°               B. α不小于45°

    C. 90°＜α＜180°                   D. α不大于90°

  5. 若△ABC三边分别为m、n、p，且，则这个三角形为（    ）

    A. 等腰三角形                    B. 等边三角形

    C. 直角三角形                    D. 等腰直角三角形

  6. 下列图形中，一定是轴对称图形的有（    ）个

    （1）角         （2）线段            （3）等腰三角形

    （4）等边三角形                （5）扇形

    （6）圆                       （7）平行四边形

    A. 4个           B. 5个           C. 6个           D. 7个

  7. 如果一个等腰三角形的一边为4cm，另一边为5cm，则它的周长为（    ）

    A. 14             B. 13              C. 14或13            D. 无法计算

  8. 下列三角形中的线段所在直线不是等腰三角形的对称轴的是（    ）

    A. 顶角的平分线                B. 一腰上的中线

    C. 底边上的中线                D. 底边上的高线

  9. 已知一个等腰三角形的两边长分别是4和8，则它的周长是（    ）

    A. 20             B. 16              C. 20或16            D. 12或16

  10. 在△ABC中，若，则△ABC一定是（    ）

    A. 等腰三角形                    B. 锐角三角形

    C. 直角三角形                    D. 钝角三角形

 

二. 填空题。

  1. 等腰三角形中一个内角为108°，则另两个内角分别为_____________。

  2. △ABC中，BA＝BC，∠C＝50°，∠A、∠C的角平分线交于D，则∠ADB＝_____________。

  3. 已知等腰三角形的一个内角为70°，则它的其余两个内角的度数分别是__________。

  4. 若两图形关于直线对称，则图形上的对应点连线段被对称轴_____________。

  5. 周长为13，边长为整数的等腰三角形共有_____________个。

  6. AD为△ABC的高，AB＝AC，△ABC周长为20cm，△ACD周长为14cm，则AD＝_____________。

  7. D、E、F分别为△ABC的边AB、BC、CA上的点，DF∥BC，BD＝DE＝EF＝FC，∠B＝30°，则∠A＝_____________。

  8. 线段AD、BC交于O，且AB＝AC，DB＝DC，AD＝3，BC＝4，则四边形ABDC的面积为_____________。

  9. 等腰三角形两腰上的高相交所成的钝角为100°，则顶角_____________，底角_____________。

  10. △ABC中，AB＝5，AC＝7，∠B、∠C的平分线交于O，直线MN过O点交AB于M、AC于N，若MN∥BC，则△AMN周长为_____________。

 

三. 解答题。

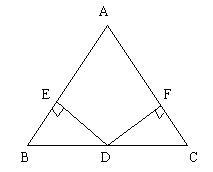
  1. 如图：△ABC中，AB＝AC，BD平分∠ABC交AC于D，∠BDC＝120°，求△ABC三个内角的度数。

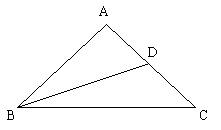
  2. 如图，△AOB中，点C在OA上，点E、D在OB上，且CD∥AB，CE∥AD，AB＝AD，试说明△CDE是等腰三角形。

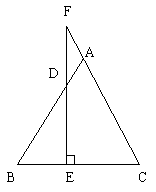
  3. 已知：如图，AB＝AC，D是AB上一点，DE⊥BC于E，ED的延长线交CA的延长线于F，那么△ADF是等腰三角形吗？为什么？

  4. 已知：如图，△ABC中，AB＝AC，D是BC的中点，DE⊥AB于E，DF⊥AC于F，写出图中所有相等的线段，并说明理由。

 

【试题答案】

一. 选择题。

  1. B            2. B               3. B               4. A               5. B

  6. C            7. C               8. B               9. A               10. D

二. 填空题。

  1. 36°，36°

  2. 115°

  3. 70°，40°或55°，55°

  4. 垂直平分

  5. 3个

  6. 4cm

  7. 30°

  8. 6

  9. 80°，50°

  10. 12

三. 解答题。

  1. 解：∵AB＝AC

    ∴∠ABC＝∠C

    又∵BD平分∠ABC

   

    设∠DBC＝x°，则∠ABC＝∠C＝2x°

    在△BDC中，∠BDC＋∠DBC＋∠C＝180°

   

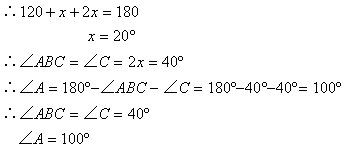
  2. 解：∵AD＝AB

    ∴∠ADB＝∠B

    又∵CD∥AB

    ∴∠CDE＝∠B

    又∵CE∥AD

    ∴∠CED＝∠ADB

    ∴∠CDE＝∠CED

    ∴CE＝CD

    ∴∠CDE是等腰三角形

  3. 解：∵AB＝AC

    ∴∠B＝∠C

    又∵DE⊥BC

    ∴∠DEB＝∠DEC＝90°

    又∵∠B＋∠DEB＋∠BDE＝∠C＋∠DEC＋∠F＝180°

    ∴∠BDE＝∠F

    又∵∠BDE＝∠FDA

    ∴∠F＝∠FDA

    ∴AD＝AF

    ∴△ADF是等腰三角形

  4. 解：图中相等的线段有：

    BD＝CD，AB＝AC，AE＝AF，DE＝DF，BE＝CF

    理由：AB＝AC是由已知可得

    又∵D是BC的中点

    ∴BD＝CD

    连结AD

    ∵AB＝AC，D是BC的中线

    ∴AD平分∠BAC

    又∵DE⊥AB，DF⊥AC

    ∴DE＝DF

    在△ADE和△ADF中

    ∠EAD＋∠AED＋∠ADE＝∠FAD＋∠AFD＋∠ADF＝180°

    ∴∠ADE＝∠ADF

    又∵AE⊥ED，AF⊥FD

    ∴AE＝AF

    又∵AB＝AC

    ∴AB－AE＝AC－AF

    ∴BE＝CF