【本讲教育信息】

一. 教学内容：

空间几何体的表面积和体积

二. 本周教学目标：

1、掌握棱柱、棱锥、棱台、圆柱、圆锥、圆台的表面积的计算公式，能直观感知空间几何体的展开图的形状，并能初步运用于实际问题之中。

2、了解棱柱、棱锥、棱台、圆柱、圆锥、圆台的体积的计算公式，能直观感知空间几何体的形状，并能初步运用于实际问题之中。

［知识要点］

一、空间几何体的表面积

问题1：有一只蚂蚁从圆柱的下底面圆周上一点A出发，沿着圆柱侧面爬行一周，到达上底面圆周上一点B（线段AB是圆柱的一条母线），问蚂蚁爬行的最短路线是多长？

平面展开图：沿着多面体的某些棱将它们展开成平面图形，这个平面图形叫做该几何体的平面展开图。

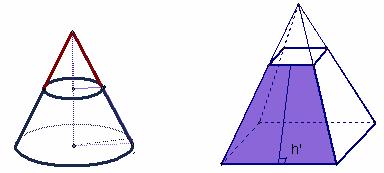
（一）棱柱、棱锥、棱台的侧面积

1、直棱柱：侧棱和底面垂直的棱柱叫做直棱柱。其侧面展开图是一个矩形。

正棱柱：底面为正多边形的直棱柱叫做正棱柱。

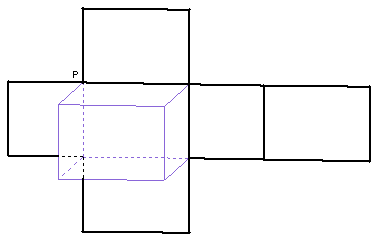
◆S_直棱柱侧＝ch其中c为棱柱的底面周长，h直棱柱的高。

2、正棱锥

定义：如果一个棱锥的底面是正多边形，并且顶点在底面的正投影是底面中心，这样的棱锥叫做正棱锥。

性质：

（1）正棱锥的侧棱长相等。

（2）侧棱和底面所成的角相等。

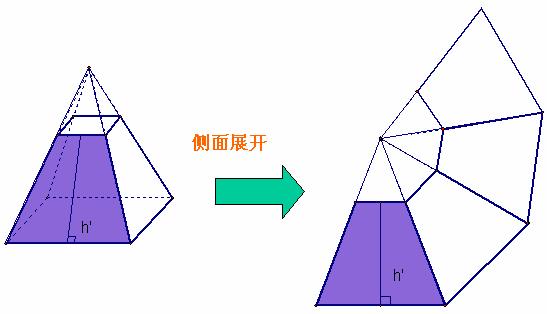
棱锥的侧面展开图是由各个侧面组成的。

◆S_正棱锥侧＝ch´（其中c为棱锥底面周长，h’为侧面等腰三角形底边上的高——斜高）

3、正棱台

定义：正棱锥被平行于底面的平面所截，截面与底面之间的部分叫做正棱台。

侧面展开图是由各个侧面组成的。

S_正棱台侧＝　（c ＋ c’）h’

（其中c，c’为棱台上下底面的周长，h’为各个等腰梯形的高，即棱台的斜高）。

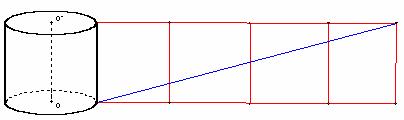
（二）、圆柱、圆锥、圆台的侧面积

把圆柱、圆锥、圆台的侧面沿着它们的一条母线剪开后展在平面上，展开图的面积就是它们的侧面积。

1、圆柱的侧面积

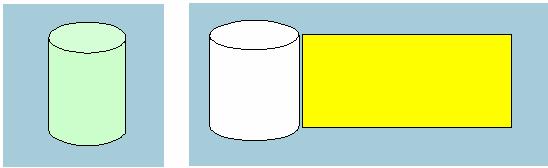
◆如果圆柱底面半径是r，周长是c，侧面母线长是l，那么它的侧面积是

2、圆锥的侧面积

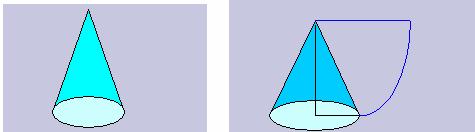
◆如果圆锥底面半径是r，周长是c，侧面母线长是l，那么它的侧面积是

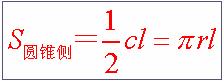
3、圆台的侧面积

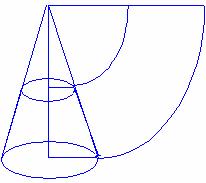
◆如果圆台的上、下面半径是周长分别是侧面母线长是，那么它的侧面积是

二、柱锥台的体积公式

长方体的体积公式是什么？如：某长方体的长宽高分别是7cm,5cm，4cm，其体积为多少，即为多少个正方体？

1、祖暅原理

两等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体的体积相等。

2、柱体的体积公式

3、锥体的体积公式

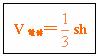
4、台体的体积计算公式

◆柱体，锥体，台体之间的关系：

5、球体的体积公式与表面积公式

（1）利用祖暅原理可得

（2）利用极限的思想推导出球的表面积公式：S_球面＝4πR²

【典型例题】

例1. 有一根长为5 cm，底面半径为1 cm的圆柱形铁管，用一段铁丝在铁管上缠绕4圈，并使铁丝的两个端点落在圆柱的同一母线的两端，则铁丝的最短长度为多少厘米？（精确到0.1 cm）

解：由题意知：BC＝5 cm，AB＝8，点A与点C就是铁丝的起止位置，故线段AC的长度即为铁丝的最短长度。AC＝

例2. 如图是一个奖杯的三视图，（单位：cm）试计算这个奖杯的体积（精确到0.01cm³）。

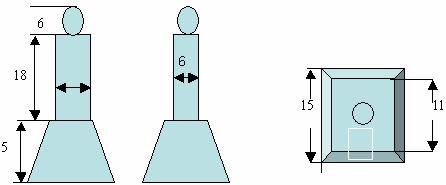
解：V_正四棱台＝

V_长方体＝6＝864

V_球 ＝

V＝ V_正四棱台 ＋ V_长方体＋ V_球

例3. 一个圆柱形的锅炉，底面直径d＝1m，高h＝2.3m。求锅炉的表面积（保留2个有效数字）。

解：底面半径r＝ S_侧面积＝ cl＝2＝ ＝2.3

S_表面积 ＝ S_侧面积＋ S_底面积＝2.3 ＋ 8.7

例4. 一个正三棱台的上下底面边长分别为3cm和6cm，高是cm，求三棱台的侧面积。

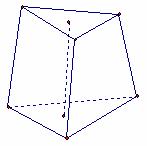
解：如图。连接AO并延长交BC于D，连结，并延长交，过作EAD于E

DE＝DO－＝，＝

S_正三棱台

【模拟试题】

一、选择题

1、下列的选项中，正确的是 （ ）

A. 侧棱不垂直于底面的棱柱不是正棱柱；

B. 侧棱垂直于底面的棱柱为正棱柱；

C. 底面是正多边形的棱柱为正棱柱；

D. 正棱柱的高可以和侧棱不相等。

2、正四棱锥的高为6，侧棱长为8，则棱锥的底面边长为 （ ）

A. B. C. D.

3、下列四个命题：（1）棱台的侧棱延长后必交于一点；（2）上、下底面为相似的正多边形的棱台一定是正棱台；（3）棱台的上、下底面边长之比等于棱台的高与截得此棱台的棱锥的高的比；（4）棱台的中截面面积等于上、下底面积之和的一半。其中正确命题的个数是（ ）。

A. 1 B. 2 C. 3 D. 4

4. 正三棱锥的底面边长为6，高为，则这个三棱锥的全面积为（ ）

A. 9 B. 18 C. 9（＋） D.

5、一个圆柱体的高不变，底面半径扩大3倍，它的体积 。

A. 扩大3倍 B. 扩大6倍 C. 扩大9倍

6、一个直角三角形，两条直角边分别长3厘米和5厘米，如果分别以这两条直角边为轴所在直线旋转一周后可以得到两个圆锥体，这两个圆锥体的体积_________。

A. 一样大

B. 以3厘米直角边为轴得到的圆锥体积大

C. 以5厘米直角边为轴得到的圆锥体积大

7、设长方体对角线长度为4，过每一顶点有两条棱与对角线夹角都是60°，则此长方体的体积为（ ）

A. B. 8 C. 8 D. 16

8、制作一个圆柱形无盖水桶，计算用多少铁皮，是求 ；计算存放这只水桶用多少空间，是求 。

A. 圆柱的侧面积 B. 圆柱的底面积

C. 圆柱的表面积 D. 圆柱的体积（容积）

E. 圆柱的侧面积＋1个圆柱的底面积

9、圆柱体的侧面积是25.12平方厘米，它的高是4厘米，它的底面半径是____。

A. 6.28厘米 B. 3.14厘米 C. 2厘米 D. 1厘米

10、柱体和一个圆锥体的底面半径和高都相等，如果圆柱体体积是30立方厘米，圆锥体体积是___立方厘米；如果圆锥体体积是30立方厘米，圆柱体体积是____立方厘米。

A. 10 B. 15 C. 30 D. 60 E. 90

二、填空题

11、球半径扩大2倍时，球面面积扩大______倍；球面体积扩大_____倍。

12、棱锥的底面面积为150cm²,平行于底面的截面面积为54cm²底面和截面距离为14cm,则这个棱锥高为_______。

13、已知三棱锥S—ABC的三条侧棱两两垂直，SA＝5，SB＝4，SC＝3，D为AB中点，E为AC中点，则四棱锥S—BCED的体积为_____。

14、正方体ABCD—A₁B₁C₁D₁中，O是上底面ABCD中心，若棱长为a，则三棱锥O—AB₁D₁的体积为 。

15、判断对错

（1）底面积相同时，圆柱越高，表面积越大、体积也越大。 __________

（2）圆锥体的体积一定是圆柱体体积的。__________

（3）圆柱体和圆锥体都有无数条高。 __________

（4）圆锥体底面半径扩大2倍，它的体积也扩大2倍。__________

三、解答题

16、已知正三棱锥的高，斜高，求经过的中点平行于底面的截面的面积。

17、若一个六棱锥的高为10cm,底面是边长为6cm的正六边形，求这个六棱锥的体积。

18、正三棱台下底面和侧面所成的二面角为60°，下底面边长为10cm,棱台的全面积为60cm²，求上底面边长。

【试题答案】

一、选择题

1、A 2、C 3、A 4、C 5、C 6、B 7、B 8、E，D 9、D 10、AE

二、填空题

11、4，8 12、35cm   13、 14、

15（1）√ （2）× （3）× （4）×

三、解答题

16、解：连结，在中，。

∵棱锥是正三棱锥，∴是中心，

∴，

，

由棱锥截面性质得：，

∴。

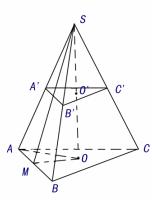
17、提示：根据题意，主要是求底面正六边形的面积，可以把正六边形分成6个全等的等边三角形，只需求一个正三角形面积即可。答案：

18、分析：正棱台上、下底面中心连线垂直于两底面，上、下底中心连线和上、下底边心距及斜高组成直角梯形，将相关元素转化到平面直角梯形来求解。

解：如图所示，

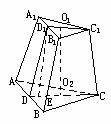
设上底面边长为x，O₁、O₂为上、下底面中心

连C₁O₁并延长交A₁B₁于D₁，连CO₂并延长交AB于D

则C₁D₁⊥A₁B₁，CD⊥AB，∠D₁DC是侧面和底面所成的二面角的平面角，∠D₁DC＝6O°

过D₁作D₁E⊥CD于E，在Rt△D₁DE中

又∵S_全＝S_上＋S_下＋S_侧 即

解得：