![]()
【本讲教育信息】
一. 教学内容:
第四章 图形的初步认识复习课
[学习要求]
1. 直观认识立体图形,视图和展开图。
2. 直观认识平面图形,了解图形的分割和组合。
3. 正确理解两点间的距离,点到直线的距离。
4. 掌握点、线段、直线、射线的表示方法。
5. 认识线段间的数量关系。
6. 理解角的两种定义。
7. 认识角与角之间的数量关系。
8. 了解同位角、内错角、同旁内角的概念,并学会识别。
9. 会识别平行线,会根据图形中的已知条件,通过简单说理,得出欲求结果。
[知识内容]
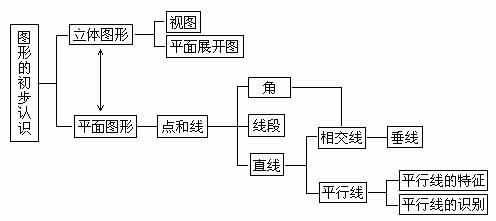
(一)生活中的立体图形
本节所学习的立体图形仅限于柱体、锥体和球体的一部分。
1. 柱体的分类与特征
(1)圆柱:底面是圆,侧面是曲面。
(2)棱柱:底面是三角形(三棱柱),侧面是正方形或长方形。
底面是四边形(四棱柱),侧面是正方形或长方形。
底面是五边形(五棱柱),侧面是正方形或长方形。
底面是六边形(六棱柱),侧面是正方形或长方形。
其中正方体的底面是正方形,并且每条棱都相等。
2. 锥体的分类与特征
(1)圆锥:底面是圆,侧面是曲面。
(2)棱锥:底面是三角形(三棱锥),侧面是三角形。
底面是四边形(四棱锥),侧面是三角形。
底面是五边形(五棱锥),侧面是三角形。
底面是六边形(六棱锥),侧面是三角形。
3. 多面体与欧拉公式
多面体:围成立体图形的面是平的面。
欧拉公式:顶点数+面数-棱数=2
即:![]()
式中V是多面体的顶点数,F是面数,E是棱数。
(二)画立体图形
画立体图形,采用的是常见的正投影,即当光线与投影垂直时的投影。
1. 什么是三视图
(1)就是从正面、上面和侧面(左面或右面)三个不同的方向看一个物体,然后描绘三张所看到的图,即视图。这样就把一个物体转化为平面的图形,即视图法。
(2)我们从不同的方向观察同一物体时,可能看到不同的图形,其中把从正面看到的图形叫做正视图(或主视图);从上面看到的图形叫做俯视图;从侧面看到的图形叫做侧视图,依观看的方向不同,有左视图、右视图。
(3)视图法是画立体图形的一种方法。
2. 由立体图形到视图的画法
(1)三视图如下的投影对应关系:
如图所示为一长方体的三视图,可发现它有如下投影关系:
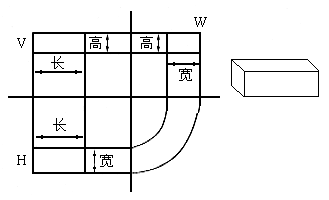
上图为一长方体的三视图,我们会发现三视图有如下投影关系:
V、H面投影:长对正,
V、W面投影:高平齐,
H、W面投影:宽相等。
对视图而言,可以说成:
正视图,俯视图:长对正,
正视图,左视图:高平齐,
俯视图,左视图:宽相等。
可简单记为口诀:正、俯长对正;正、左高平齐;俯、左宽相等。
(2)如何画三视图?
先分别从正面、上面、左面看是什么图形,再注意:正视图和俯视图“长对正”;正视图和左视图要“高平齐”。再就是注意,俯视图和左视图要“宽相等”,这样才能正确地画出简单的立体图形的三视图。
3. 由视图到立体图形(即读图)
由视图到立体图形,根据视图想像出视图反映的物体的立体形状,我们称为读图。读图的一般知识:①长、宽、高的关系:正视图和俯视图的长度相等,正视图和左视图高度相等,俯视图和左视图的宽度相等。②上、下、前、后、左、右的关系:读图时,可从正视图上分清物体各部分的上、下和左、右的位置;从俯视图上分清物体各部分的左、右和前、后的位置;从左视图上分清物体的上、下和前、后的位置。
(三)立体图形的展开图
1. 由多面体求平面展开图
(1)设想沿着多面体的一些棱将它剪开,可以把多面体展开成一个平面图形。通过自己动手操作,经历和体验图形的变化过程,可以发现一个多面体会有不同的展开方式,而且按不同的展开方式展开,可以得到不同的平面展开图。
(2)由什么多面体展开而成的平面图形,就叫做什么多面体的平面展开图。
2. 由平面展开图判断多面体
可把平面展开图复制下来,通过亲手折叠,就可发现是什么多面体了。
(四)平面图形
1. 圆的定义
圆:是由曲线组成的封闭图形。
2. 多边形的定义
(1)多边形:由一些线段首尾顺次相接所组成的封闭图形。
(2)多边形的名称:按照组成多边形的边数,多边形可分为三角形、四边形、五边形,……
(3)多边形的分割
n边形从一个顶点出发可作![]() 条对角线,将n边形分成
条对角线,将n边形分成![]() 个三角形。
个三角形。
(五)最基本的图形——点和线
点和线是两个最基本的图形,线段是最基本最原始的概念,由“线段”引入“射线”“直线”。
1. 线段、射线、直线的区别
|
|
线段 |
射线 |
直线 |
|
图形 |
|
|
|
|
表示方法 |
线段AB(BA)或线段a(字母无序) |
射线OA(字母有序) |
直线AB(BA)或直线a(字母无序) |
|
端点 |
两个 |
一个 |
无 |
|
长度 |
可度量长度 |
无 |
无 |
|
延伸方向 |
不向任何一方延伸 |
向OA方向无限延伸 |
向两方无限延伸 |
2. 线段和直线的基本性质(公理)
(1)线段公理:两点之间,线段最短。
(2)两点间的距离:连接两个点的线段的长度。
(3)线段的中点:把一条线段分成两条相等线段的点。
(4)直线公理:经过两点有一条直线,并且只有一条直线。
3. 线段的大小比较方法
比较线段的大小方法可有两种:叠合法与度量法。
(六)角
1. 角的两种定义
角是由两条有公共端点射线组成的图形,角也可以看成是由一条射线绕着它的端点旋转而成的图形。
2. 角的表示方法
角的表示方法有三种:
(1)用三个大写字母表示。
(2)当角的顶点处只有一个角时,用一个大写字母表示。
(3)用一个数字或一个希腊字母表示。
3. 角的分类

4. 角的度量及角的大小比较
(1)角的度量用度、分、秒制。![]() 。
。
(2)角的大小比较,有叠合法和度量法两种方法。
5. 角的特殊关系
(1)若![]() ,则α、β互为余角。
,则α、β互为余角。
(2)若![]() ,则α、β互为补角。
,则α、β互为补角。
(3)同角(或等角)的余角相等。
(4)同角(或等角)的补角相等。
(5)对顶角的性质:对顶角相等。
6. 角的平分线
角平分线:从一个角的顶点引出的一条射线,把这个角分成两个相等的角。
7. 画一个角等于已知角
画一个角等于已知角有两种方法:量角器法与圆规直尺法。
8. 如何表示方向
象限角:以正北或正南方向到被测目标之间的夹角。
(七)相交线
1. 垂线的定义及其性质
(1)定义:当两条直线相交所成的四个角中,有一个角是直角时,就叫这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫垂足。
(2)性质
①经过直线外或直线上一点,有且只有一条直线与已知直线垂直。
②从直线外一点到这条直线的所有线段中,垂线段最短。
2. 垂线段和点到直线的距离的概念
(1)垂线段:过直线外一点画这条直线的垂线以这点和垂足为端点的线段。
(2)点到直线的距离:从直线外一点到这条直线的垂线段的长度。
3. 同位角、内错角、同旁内角的特征
(1)同位角特征![]()
(2)内错角特征![]()
(3)同旁内角特征![]()
(八)平行线
1. 平行线的定义与平行公理
(1)平行线:在同一平面内不相交的两条直线。
(2)平行公理:经过已知直线外一点,有且只有一条直线与已知直线平行。
2. 平行线的识别方法
(1)同位角相等,两直线平行。
(2)内错角相等,两直线平行。
(3)同旁内角互补,两直线平行。
(4)垂直于同一条直线的两条直线互相平行。
(5)平行于同一条直线的两条直线互相平行。
3. 平行线的特征
(1)两直线平行,同位角相等。
(2)两直线平行,内错角相等。
(3)两直线平行,同旁内角互补。
4. 一个角的两边与另一个角的两边的平行与垂直关系
(1)一个角的两边与另一个角的两边分别平行,这两个角相等或互补。
当一个角的两边与另一个角的两边方向都相同或都相反时,这两个角相等;当一个角的两边与另一个角的两边一组方向相同而另一组方向相反时,这两个角互补。
(2)一个角的两边与另一个角的两边分别垂直,这两个角相等或互补。
5. 常见的几种两条直线平行或垂直的结论
(1)两条平行线被第三条直线所截,一组同位角的角平分线互相平行。
(2)两条平行线被第三条直线所截,一组内错角的角平分线互相平行。
(3)两条平行线被第三条直线所截,一组同旁内角的角平分线互相垂直。
(4)一组邻补角的角平分线互相垂直。
【典型例题】
例1. 下列说法中错误的序号是( )
①球体不是多面体;②柱体都是多面体;③圆锥是多面体;④棱柱、棱锥都是多面体。
A. ①② B. ①④ C. ②③ D. ③④
解:选A
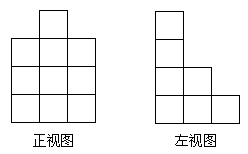
例2. 由几个小正方体所搭成的几何体的俯视图如下图所示,小正方形中的数字表示该位置的小正方体的个数,请你画出这个几何体的正视图和左视图。
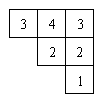
解:
例3. 下面的第一个长方形已经被直线划分,利用这个已经给出的图形,看一看在每个图形中,黑色部分各占整个图形的多少?用最简单的分数形式将答案表示出来。

解:由图可知:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ;
;
(5)![]() ;(6)
;(6)![]() ;(7)
;(7)![]() ;(8)
;(8)![]() ;
;
(9)![]() ;(10)
;(10)![]() ;(11)
;(11)![]()
例4. 已知线段![]() ,在直线AB上有一点C,且
,在直线AB上有一点C,且![]() ,M为线段AC的中点。求线段AM的长。
,M为线段AC的中点。求线段AM的长。
分析:题目中只说明A、B、C三点共线,但无法判断点C是在线段AB上,还是在线段AB的延长线上,所以要分两种情况来求AM的长。
解:(1)当点C在线段AB上时,如图所示:
![]()
∵M是AC的中点
![]()
又![]()
![]()
(2)当点C在线段AB的延长线上时,如图所示:
![]()
∵M是AC的中点
![]()
又![]()
![]()
答:综合(1)、(2)可知,AM的长度为2 cm或6 cm。
点评:当题目中条件不能确切判断是哪一种位置关系时,要对所有可能的位置关系进行考虑。
例5. 把一张长方形纸条按如图所示那样折叠后,若得到∠AOB'=50°,则∠B'OG的度数是多少?你能用推理的方法求出来吗?
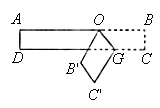
解:由题意知∠B'OG=∠BOG
又∠BOB'=∠B'OG+∠BOG=2∠B'OG=180°-50°=130°
![]()
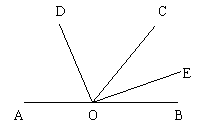
例6. (1)如图,O是直线AB上一点,OD平分∠AOC,OE平分∠COB,请找出与∠COE互余的角。
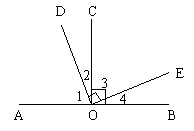
(2)如图,CO⊥AB,OD⊥OE,则图中共有互余的角的对数是__________。
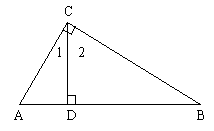
(3)如图,∠ACB=90°,CD⊥AB,则图中互余的角有_______对。
解:(1)与∠COE互余的角有∠COD、∠AOD
理由如下:
∵∠AOC+∠BOC=180°
又OE平分∠BOC,OD平分∠AOC

(2)4对
分别是∠1与∠2、∠2与∠3、∠3与∠4、∠1与∠4互余。
(3)4对
分别是∠A与∠1、∠1与∠2、∠2与∠B、∠A与∠B互余。
下图中,条件同(2),试说出图中共有几对互余的角(答案:6对)
下图中,∠ACB=90°,CD⊥AB于点D,DE⊥AC于点E,图中互余的角共有多少对(答案:8对)

例7. 如图,AB∥CD,EO与FO相交于点O,试猜想∠1、∠2、∠3之间的关系,并说明理由。
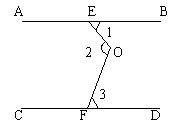
解:过O作MN∥AB
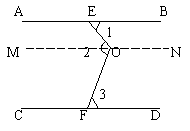
∵AB∥CD
∴AB∥MN∥CD(两直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠1=∠EOM,∠3=∠FOM
∴∠1+∠3=∠EOM+∠FOM=∠EOF=∠2
∴∠2=∠1+∠3
例8. 已知:如图,CD⊥AB,垂足为D,点F是BC上任意一点,FE⊥AB,垂足为E,且∠1=∠2=30°,∠3=84°,求∠4的度数。
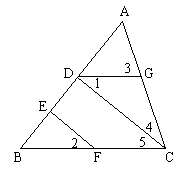
分析:把CD⊥AB,FE⊥AB在图形中标出后,不难看出EF∥CD,由∠1=∠2,∠5=∠2,又得DG∥BC,再利用平行线的性质求∠4。
解:∵CD⊥AB,FE⊥AB(已知)
∴∠CDB=∠FEB=90°(垂直的定义)
∴CD∥FE(同位角相等,两直线平行)
∴∠5=∠2(两直线平行,同位角相等)
∵∠1=∠2(已知)
∴∠5=∠1=30°(等量代换)
∴DG∥BC(内错角相等,两直线平行)
∴∠BCA=∠3=84°(两直线平行,同位角相等)
∴∠4=∠BCA-∠5=84°-30°=54°
说明:(1)本例综合运用了平行线的判定与性质,运用时必须分清“判定”与“性质”的区别,避免因果倒置。
(2)可用“垂直于同一直线的两直线也互相平行”直接证CD∥FE。
【模拟试题】(答题时间:70分钟)
一. 选择题。
1. 下列图形,( )都是柱体。
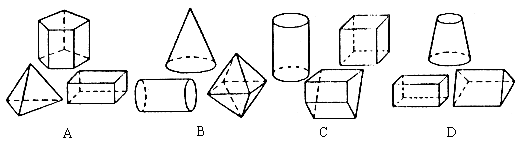
2. 下列图形中,( )是四棱锥的三视图。
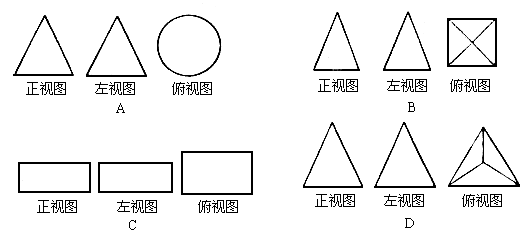
3. 下列说法正确的是( )
A. 两点之间,直线最短。
B. 大于直角的角叫做钝角。
C. 若两个角互为余角,则这两个角不可能相等。
D. 一个锐角的补角比这个锐角的余角大90°。
4. 三条直线相交于一点,构成对顶角是( )
A. 4对 B. 5对 C. 6对 D. 7对
5. 下列说法正确的是( )
A. 两直线被第三条直线所截,同旁内角互补。
B. 平行线中同位角的平分线互相平行。
C. 相等的角是平行线所得的内错角。
D. 从直线外一点到这条直线的垂线段叫做点到直线的距离。
6. 如图(1),AB∥CD,那么∠A+∠E+∠F+∠C等于( )
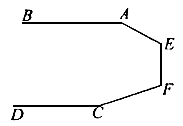
图(1)
A. 540° B. 360° C. 720° D. 270°
7. 下列命题中正确的是( )
A. 两直线相交所成四个角中有两个相等,那么这两条直线垂直。
B. 两直线相交所成四个角中两对角相等,则这两条直线垂直。
C. 两条直线相交所成四个角中若有两个角互补,则这两直线垂直。
D. 两条直线相交所成四个角中有两个对顶角互补,则这两直线垂直。
8. 如图(2),![]() ,图中与∠α相等的角有( )
,图中与∠α相等的角有( )
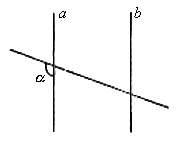
图(2)
A. 1个 B. 2个 C. 3个 D. 4个
9. 如图(3),下列条件中不能判断AB∥CD的是( )
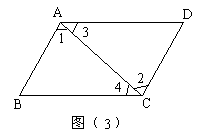
A. ∠3=∠4
B. ∠1=∠2
C. ∠B+∠BCD=180°
D. ∠D+∠BAD=180°
10. 如图(4),BE平分∠ABC,DE∥BC,图中相等的角共有( )

图(4)
A. 3对 B. 4对 C. 5对 D. 6对
二. 填空题。
11. 把下列图形的名称填在括号内:
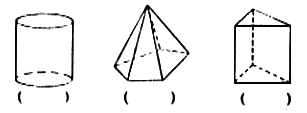
12. 一个多面体有12条棱,6个顶点,则这个多面体是________面体。
13. 下列图形是某些立体图形的平面展开图,说出这些立体图形的名称:
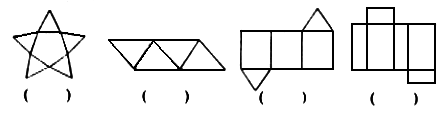
14. 按角的位置关系填空,如图(5),∠A与∠1是_____________;∠A与∠3是____________;∠2与∠3是____________。

图(5)
15. 如图(6),∠ABC=120°,∠BCD=85°,AB∥ED,则∠CDE=________。
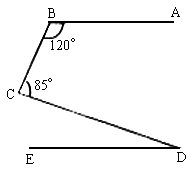
图(6)
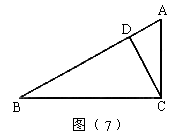
16. 如图(7),AC⊥BC,CD⊥AB,D为垂足,图中有__________个直角,点C到直线AB的距离是__________。
17. 计算:29°30′=___________°
18.25°=___________°___________′
23°45′+24°20′=___________
56°15′-32°28′=___________
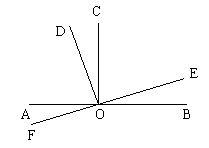
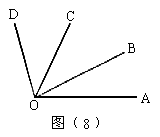
18. 如图(8)所示,图中小于平角的角有__________个,把它们分别表示出来__________
__________________________________________________。
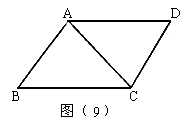
19. 如图(9)所示,如果∠__________=∠__________,那么根据____________________
____________________,可得AB∥CD;如果AD∥BC,那么根据______________,可得∠__________+∠__________=180°。
20. 每过1 min,时钟的分针转了__________度的角,时针转了__________度的角。
三. 作图题。
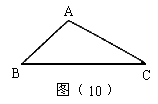
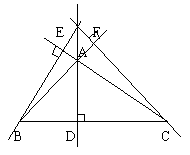
21. 如图(10),已知△ABC,按下列要求画图。
(1)过A作BC的垂线AD;
(2)过C作AB的垂线CE;
(3)过B作AC的垂线BF。
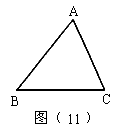
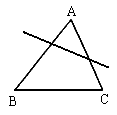
22. 如图(11),在△ABC所在平面中画一条直线,使得与∠A成同旁内角的角有4个。
四. 解答题。
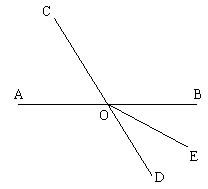
23. 如图所示,直线AB、CD交于O,OE平分∠BOD,若∠AOC∶∠BOC=2∶3,求∠DOE的度数。
![]()
【试题答案】
一. 选择题。
1. C 2. B 3. D 4. C 5. B
6. A 7. D 8. C 9. A 10. C
二. 填空题。
11. 圆柱;五棱锥;三棱柱
12. 八
13. 五棱锥;四面体;三棱柱;长方体
14. 同旁内角;同位角;内错角
15. 25°
16. 3;线段CD的长
17. 29.5°;18°15′;48°5′;23°47′
18. 6;∠AOB;∠AOC;∠AOD;∠BOC;∠BOD;∠COD
19. ∠BAC;∠ACD;内错角相等,两直线平行;两直线平行,同旁内角互补;∠DAB;∠B(或∠BCD;∠D)
20. 6;0.5
三. 作图题。
21.
22.
四. 解答题。
23. 解:∵∠AOC+∠BOC=180°
∠AOC∶∠BOC=2∶3
∴∠AOC=72°,∠BOC=108°
∵∠BOD=∠AOC
∴∠BOD=72°
又∵OE平分∠DOB
![]()