一. 本周教学内容：

弧长和扇形面积公式、圆锥的侧面积和全面积

教学目的

1. 使学生掌握弧长和扇形面积公式、圆锥及其特征，使学生掌握圆锥的轴截面图及其特点。

2. 使学生掌握弧长和扇形面积公式、圆锥侧面展开图的画法及侧面积计算公式。

3. 使学生比较熟练地应用弧长和扇形面积公式、圆锥的基本性质和轴截面解决有关圆锥表面积的计算问题。

4. 培养学生空间观念及空间图形与平面图形的相互转化思想，培养学生空间想象能力和计算能力。

教学重点和难点：

教学重点是弧长和扇形面积公式，圆锥及其特征，圆锥的侧面积计算

难点是圆锥侧面展开图（扇形）中各元素与圆锥各元素之间的关系

教学过程

1. 圆周长：

圆面积：

2. 圆的面积C与半径R之间存在关系，即360°的圆心角所对的弧长，因此，1°的圆心角所对的弧长就是。

n°的圆心角所对的弧长是

P₁₂₀

*这里的180、n在弧长计算公式中表示倍分关系，没有单位。

3. 由组成圆心角的两条半径和圆心角所对的弧所围成的圆形叫做扇形。

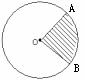
发现：扇形面积与组成扇形的圆心角的大小有关，圆心角越大，扇形面积也就越大。

4. 在半径是R的圆中，因为360°的圆心角所对的扇形的面积就是圆面积，所以圆心角为n°的扇形面积是：

（n也是1°的倍数，无单位）

5. 圆锥的概念

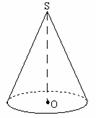
观察模型可以发现：圆锥是由一个底面和一个侧面围成的。其中底面是一个圆，侧面是一个曲面，如果把这个侧面展开在一个平面上，展开图是一个扇形。

如图，从点S向底面引垂线，垂足是底面的圆心O，垂线段SO的长叫做圆锥的高，点S叫做圆锥的顶点。

锥也可以看作是由一个直角三角形旋转得到的。也就是说，把直角三角形SOA绕直线SO旋转一周得到的图形就是圆锥。其中旋转轴SO叫做圆锥的轴，圆锥的轴通过底面圆的圆心，并且垂直于底面。另外，连结圆锥的顶点和底面圆上任意一点的线段SA、SA₁、SA₂、……都叫做圆锥的母线，显然，圆锥的母线长都相等。

母线定义：连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线。P₁₂₂

6. 圆锥的性质

由图可得

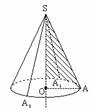
（1）圆锥的高所在的直线是圆锥的轴，它垂直于底面，经过底面的圆心；

（2）圆锥的母线长都相等

7. 圆锥的侧面展开图与侧面积计算

圆锥的侧面展开图是一个扇形，这个扇形的半径是圆锥侧面的母线、圆心是圆锥的顶点、弧长是圆锥底面圆的周长。

圆锥侧面积是扇形面积。

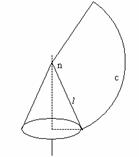
如果设扇形的半径为l，弧长为c，圆心角为n（如图），则它们之间有如下关系：

同时，如果设圆锥底面半径为r，周长为c，侧面母线长为l，那么它的侧面积是：

圆锥的全面积为：

圆柱侧面积：。

例：在⊙中，120°的圆心角所对的弧长为，那么⊙O的半径为___________cm。

答案：120

解：由弧长公式：得：

例：若扇形的圆心角为120°，弧长为，则扇形半径为_____________，扇形面积为____________________。

答案：15；25π

例：如果一个扇形的面积和一个圆面积相等，且扇形的半径为圆半径的2倍，这个扇形的中心角为____________。

答案：90°

例：已知扇形的周长为28cm，面积为49cm²，则它的半径为____________cm。

答案：7

例：两个同心圆被两条半径截得的，，又AC=12，求阴影部分面积。

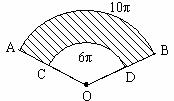
解：设OC=r，则OA=r+12，∠O=n°

∴OC=18，OA=OC+AC=30

例：如图，已知正方形的边长为a，求以各边为直径的半圆所围成的叶形的总面积。

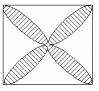
解：∵正方形边长为a

∴，

∴叶的总面积为

*也可看作四个半圆面积减去正方形面积

例：已知AB、CD为⊙O的两条弦，如果AB=8，CD=6，的度数与的度数的和为180°，那么圆中的阴影部分的总面积为？

解：将弓形CD旋转至B，使D、B重合

如图，C点处于E点

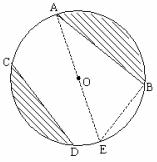
的度数为180°

∴AE是⊙O的直径

∴∠ABE=90°

又∵AB=8，BE=CD=6

由勾股定理

∴半径

例：在△AOB中，∠O=90°，OA=OB=4cm，以O为圆心，OA为半径画，以AB为直径作半圆，求阴影部分的面积。

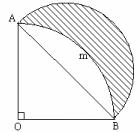
解：∵OA=4cm，∠O=90°

∴

，

则阴影部分的面积为：

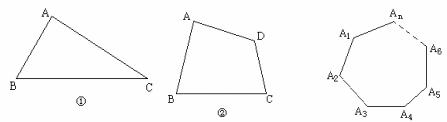
例：①、②……是边长均大于2的三角形，四边形、……、凸n边形，分别以它们的各顶点为圆心，以1为半径画弧与两邻边相交，得到3条弧，4条弧，……

（1）图①中3条弧的弧长的和为_________________

图②中4条弧的弧长的和为_________________

（2）求图中n条弧的弧长的和（用n表示）

解：（1）π，2π

（2）解法1：

∵n边形内角和为：（n－2）180°

前n条弧的弧长的和为：个以某定点为圆心，以1为半径的圆周长

∴n条弧的弧长的和为：

解法2：设各个扇形的圆心角依次为

则

∴n条弧长的和为：

例：如图，在Rt△ABC中，已知∠BCA=90°，∠BAC=30°，AC=6m，把△ABC以点B为中心逆时针旋转，使点C旋转到AB边的延长线上的点C'处，那么AC边扫过的图形（阴影部分）的面积为？

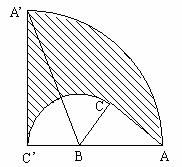
分析：在Rt△ACB中，∠C=90°，∠BAC=30°，AB=6

法一：

法二：以B为圆心，BC为半径画弧

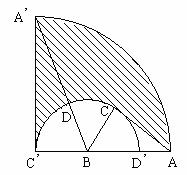
交A'B于D，AB于D'

有，

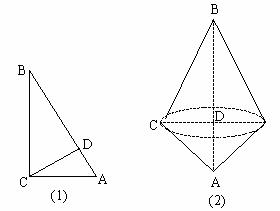
例：如图，已知Rt△ABC的斜边AB=13cm，一条直角边AC=5cm，以直线AC为轴旋转一周得一个圆锥。求这个圆锥的表面积。如果以直线AB为轴旋转一周，能得到一个什么样的图形？

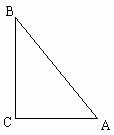
解：

以直线AC为轴旋转一周所得的圆锥如图所示，它的表面积为：

以直线AB为轴旋转一周，所得到的图形如图所示。

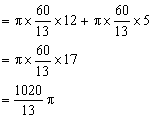
例：一个圆锥的模型，这个模型的侧面是用一个半径为9cm，圆心角为240°的扇形铁皮制作，再用一块圆形铁皮做底，则这块图形铁皮的半径为______________。

答案：6

例：若圆锥的轴截面是一个边长为2cm的等边三角形，则这个圆锥的侧面积是_______。

答案：2π

例：已知圆锥的底面半径为40cm，母线长为90cm，则它的侧面展开图的圆心角为______。

答案：160°

例：若圆锥的侧面积是底面积的2倍，则侧面展开图的圆心角是__________。

答案：180°

例：如图，圆锥形的烟囱帽的底面直径是80cm，母线长50cm。

（1）画出它的展开图；

（2）计算这个展开图的圆心角及面积。

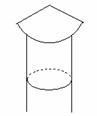
解：（1）烟囱帽的展开图是扇形，这个扇形的半径是圆锥的母线长，弧长是圆锥底面周长（如图）

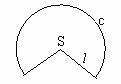
（2）设扇形的半径为l，弧长为c，圆心角为α，则l=50cm，

=288（度）

例：一个圆锥的高是10cm，侧面展开图是半圆，求圆锥的侧面积。

解：设圆锥底面半径为r，圆锥母线长为l，扇形弧长（即半圆）为c，则由题意得

即

在Rt△SOA中，

由此求得

故所求圆锥的侧面积为

例：蒙古包可以近似地看作圆锥和圆柱组成，如果想用毛毡搭建20个底面积为，高为3.5m，外围高4m的蒙古包，至少要多少平方米的毛毡？

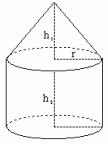
解：

∵h₁=4，∴

答：至少要平方米的毛毡。

【模拟试题】

［基础演练］

1. 已知扇形的弧长为6πcm，圆心角为60°，则扇形的面积为____________。

2. 已知弓形的弧所对的圆心角为60°，弓形弦长为a，则这个弓形的面积是__________。

3. 如图，在平行四边形ABCD中，，，BD⊥AD，以BD为直径的⊙O交AB于E，交CD于F，则图中阴影部分的面积为___________。

4. 如图，AB是⊙O₁的直径，AO₁是⊙O₂的直径，弦MN//AB，且MN与⊙O₂相切于C点，若⊙O₁的半径为2，则O₁B、、CN、所围成的阴影部分的面积是_____________。

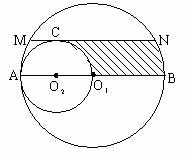
5. 如图，△ABC为某一住宅区的平面示意图，其周长为800m，为了美化环境，计划在住宅区周围5m内，（虚线以内，△ABC之外）作绿化带，则此绿化带的面积为___________。

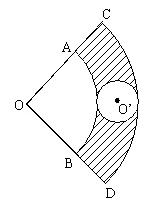
6. 如图，两个同心圆被两条半径截得的，，⊙O'与，都相切，则图中阴影部分的面积为____________。

［综合测试］

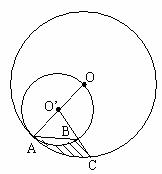
7. 如图，OA是⊙O的半径，AB是以OA为直径的⊙O’的弦，O’B的延长线交⊙O于点C，且OA=4，∠OAB=45°，则由，和线段BC所围成的图形面积是______。

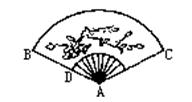
8. 如图，一扇形纸扇完全打开后，外侧两竹条AB，AC的夹角为120°，AB长为30cm，贴纸部分BD长为20cm，贴纸部分的面积为（ ）

A. B.

C. D.

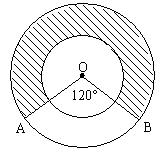
9. 如图，在同心圆中，两圆半径分别为2、4，∠AOB=120°，则阴影部分的面积为（ ）

A. B. C. D.

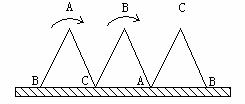
10. 一块等边三角形的木板，边长为1，现将木板沿水平翻滚（如图），那么，B点从开始至结束所走过的路径长度为（ ）

A. B. C. 4 D.

11. （2004·湖北黄冈）如图，要在直径为50cm的圆形木板上截出四个大小相同的圆形凳面，问怎样才能截出直径最大的凳面，最大直径是多少厘米？

［探究升级］

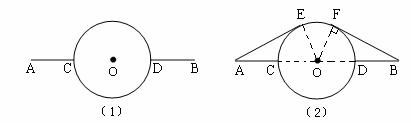
12. （2004·新疆）在相距40km的两个城镇A、B之间，有一个近似圆形的湖泊，其半径为10km，圆心恰好位于A、B连线的中点处，现要绕过湖泊从A城到B城，假设除湖泊外，所有的地方均可行走，有如图所示两种行走路线，请你通过推理计算，说明哪条路线较短。

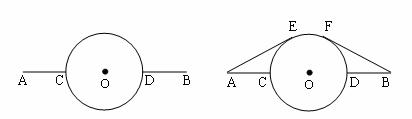
（1）的路线：线段线段DB

（2）的路线：线段线段FB（其中E、F为切点）

【试题答案】

1. 2.

3. 4.

5. 6.

7.

8. A 9. B 10. B

11. 截法如图所示

根据圆的对称性可知：

O₁，O₃都在⊙O的直径AB上，设所截出的凳面的直径为r

则O₁O₂=r，O₂O₃=r，

又

12. 由题意可知图答（1）路径：

图答（2）路径：如图连接OE、OF，连结CD

由题意可知A、C、D、B共线，且经过O点

∵E为切点，∴OE⊥AE

在Rt△OAE中，AO=2EO

∴∠A=30°，∠AOE=60°

同理∠BOF=60°

同理

由计算可知图（2）路线较短。

【励志故事】

神奇的皮鞋

多明尼奎·博登纳夫，是法国一位年轻的企业家、艺术家。他所经营的公司历来就是发展美术业，但始终都是没有看到兴旺的一天。

一天，他在徒步回家的路上，突然，感到脚下有什么绊了一下，低头一看，原来是一只破旧皮鞋，他刚想抬起脚将它踢开，却又发现这只鞋有几分像一张皱纹满布的人脸。一个艺术的灵感刹那间在他脑海里闪现，他如获至宝，于是赶忙将破旧皮鞋拾起，迫不及待地跑回家，将其改头换面，变成了一件有鼻有眼有表情的人像艺术品。

以后，博登纳夫又陆续捡回一些残旧破皮鞋，经过他那丰富的想象力和神奇的艺术之手再加工，一双双被遗忘的“废物”先后变成奇妙谐趣的皮鞋脸谱艺术品。后来，博登纳夫在巴黎开设了皮鞋人像艺术馆，引起了轰动，生意异常兴隆。

看来，在现实生活中，在许多人不屑一顾的小小事情里，往往都隐藏着成功的契机。当然，要获得成功，得靠用心发掘。博登纳夫的这一成功，无疑就在于他比别人多了一个“艺术”心眼。