![]()
【同步教育信息】
一. 本周教学内容:
丰富的图形世界 (一)
二. 教学目标:
(1)会辨认基本几何体(直棱柱、圆柱、圆锥、球等);
(2)了解直棱柱、圆柱、圆锥的侧面展开图,能根据展开图判断和制作立体模型;
(3)能想象基本几何体的截面形状;
(4)会画基本几何体的三视图,会判断简单物体的三视图,能根据三视图描述几何体或实物原型;
(5)能从丰富的现实背景中抽象出空间几何体和基本平面图形,进一步认识点、线、面。
三. 教学过程:
立体图形:
1)像长方体、正方体、球体、圆柱体、圆锥体等都是立体图形。
2)还有一些立体图形:帐篷、螺母给我们的形象是棱柱的形象,金字塔给我们的形象是棱锥的形象。
棱柱、长方体、正方体的关系:

3)认识简单的常见平面图形,如三角形、四边形、五边形等多边形和圆。会判断一个复杂的平面图形中包含了哪些简单图形。
4)从观察到的实物中常见立体图形:柱体包括圆柱和棱柱;锥体包括圆锥和棱锥;及球体
5)平面图形:像长方形、正方形、三角形、圆等图形都是平面图形。
6)由几个立方体组成正多面体,如:正八面体,正二十面体。
7)展开图:许多立体图形是由一些平面图形围成的,将它们适当剪开就可以展开成平面图形。
【典型例题】
例1:填空:
(1)长方体、正方体都有 个面,长方体的6个面可能都是 形,也有可能都有2个面是 形, 它的
面完成相同。
答:6个面,长方形,正方形,对
(2)正方体的6个面都是 形,6个面的面积是
。
答:正方形,相等
(3)圆柱的上、下底面是 ;
(4)圆锥的底面是
答:圆,圆
例2:填空:
(1)三棱柱的上、下底面是 ;侧面是 。
答:三角形,四边形
(2)四棱柱的上、下底面是 ;侧面是 。
答:四边形 四边形
例3:一个三棱柱的底面边长为acm,侧棱长为bcm。(1)这个三棱柱共有几个面?它们分别是什么形状?哪些面的形状、面积完全相同? (2)这个三棱柱共有多少条棱,它们的长度分别是多少?
答:(1)5个面,其中3个侧面是长方形,两个底面是三角形,两个底面形状完全相同,三个侧面形状完全相同。
(2)共有9条棱,其中侧棱长均为bcm,底面棱长均为acm.
例4:图中的两个图形经过折叠能否围成棱柱?先想一想,再试一试。
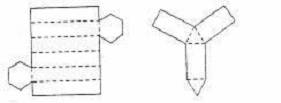
答:都可以,第一个可以围成六棱柱;第二个可以围成三棱柱
例5:将一个正方体的表面沿某些棱剪开,展成一个平面图形,把你展开后的不同平面图形都画出来,看看有几种。
答:
1)
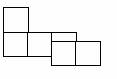
2)
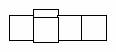
3)
![]()
例6:两位同学用图形画出的小动物中,哪个图形是用立体图形组成的?用了哪些立体图形?哪个图形是用平面图形组成的?用了哪些平面图形?
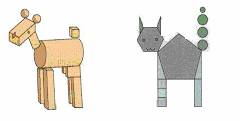
答:第一个图形是由圆柱体、长方体、球体、正方体组成;第二个图形是由三角形、长方形、五边形、六边形、圆组成。
【模拟试题】(答题时间:40分钟)
1. 判断正误
(1)圆柱的上下两个面一样大 ( )
(2)圆柱、圆锥的底面都是圆 ( )
(3)棱柱的底面是四边形 ( )
(4)棱锥的侧面都是三角形 ( )
(5)棱柱的侧面可能是三角形 ( )
(6)圆柱的侧面是长方形 ( )
(7)球体不是多面体
( )
(8)圆锥是多面体 ( )
(9)棱柱、棱锥都是多面体 ( )
(10)柱体都是多面体 ( )
2. 一个四棱柱被一刀切去一部分,试举例说明剩下的部分是否可能还是四棱柱。
3. 一个长方形的长是宽的两倍,把这长方形剪成:
(1) 两部分,使得他们能够构成一个有两条边相等的三角形;
(2) 三部分,使得能由它们构成一个正方形。
4. 把一个正方形用两条线分成大小、形状完全相同的四块,你能有几种方法?
5. 请说出分别与下列展开图对应的立体图形的名称。
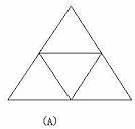
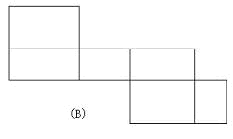
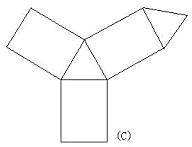
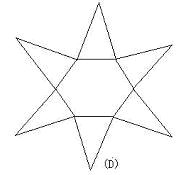
6. 哪种几何体的表面能展成下面的图形?
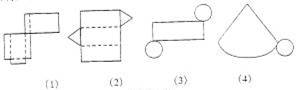
7. 图中的两个图形经过折叠能否围成棱柱?先想一想,再试一试。
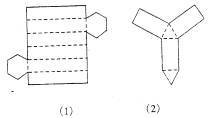
8. 看图回答下列问题:(1)这个几何体的名称(2)这个几何体有几个面,底面、侧面分别都是什么图形?(3)侧面的个数与底面多边形的边数有什么关系?(4)这个几何体有几条侧棱,它们的长度之间有什么关系?
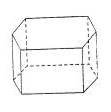
9. 将一个正方体的表面沿某些棱剪开,展成一个平面图形,把你展开后的不同平面图形都画出来,看看有几种
![]()
【试题答案】
1.(1)对、(2)对。(3)错。“应是多边形”。(4)对。(5)错。“应是四边形”。
(6)错。(7)对。(8)错。“应是旋转体”。(9)对。(10)错。“圆柱是旋转体”。
2. 可能,只要沿着平行于棱柱的侧面或底面的平面切即可,其它方法不行
3. (1)沿长的中点与对边一个端点剪,然后拼接即可(也可以沿对角线剪)

(2)沿长的中点与对边端点剪,然后拼接即可

4. 无数种。图中所示是其中一些方法,例如由中间两条线绕着他们的交点旋转可以得到其它无数种方法。

5: 分析:注意分析平面图的特点,同时结合一些常见的立体图的平面展开图,如三棱锥,三棱柱,四棱柱等等,再作出判断。
解:(A)是一个三棱锥沿侧面的棱剪开得到,(B)是一个长方体的平面展开图,(C)是三棱柱适当剪开得到,(D)是一个五棱锥的展开图,原来的立体图如下:
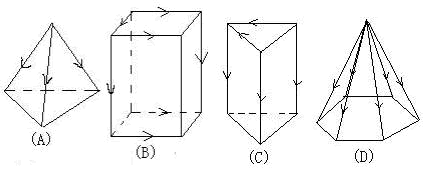
6. (1)长方体;(2)三棱柱;(3)圆柱;(4)圆锥
7.能
8. (1)六棱柱;(2)8个面,六边形和长方形;(3)相等;(4)6,相等。
9. 将其表面展成一个平面图形,其面与面之间相连的棱有5条,因此需要剪开7条
【励志故事】
神奇的皮鞋
多明尼奎·博登纳夫,是法国一位年轻的企业家、艺术家。他所经营的公司历来就是发展美术业,但始终都是没有看到兴旺的一天。
一天,他在徒步回家的路上,突然,感到脚下有什么绊了一下,低头一看,原来是一只破旧皮鞋,他刚想抬起脚将它踢开,却又发现这只鞋有几分像一张皱纹满布的人脸。一个艺术的灵感刹那间在他脑海里闪现,他如获至宝,于是赶忙将破旧皮鞋拾起,迫不及待地跑回家,将其改头换面,变成了一件有鼻有眼有表情的人像艺术品。
以后,博登纳夫又陆续捡回一些残旧破皮鞋,经过他那丰富的想象力和神奇的艺术之手再加工,一双双被遗忘的“废物”先后变成奇妙谐趣的皮鞋脸谱艺术品。后来,博登纳夫在巴黎开设了皮鞋人像艺术馆,引起了轰动,生意异常兴隆。
看来,在现实生活中,在许多人不屑一顾的小小事情里,往往都隐藏着成功的契机。当然,要获得成功,得靠用心发掘。博登纳夫的这一成功,无疑就在于他比别人多了一个“艺术”心眼。