【同步教育信息】

一. 本周教学内容：

选修2—2第二章推理与证明

二. 教学目的：

1、了解合情推理的含义，掌握演绎推理的基本模式，能利用归纳推理、类比推理和演绎推理等进行简单的推理，体会并认识它们在数学发现中的作用和重要性．

2、掌握直接证明的两种基本方法：分析法和综合法；了解分析法和综合法的思考过程与特点．

3、掌握间接证明的一种基本方法―反证法；了解反证法的思考过程、特点．

4、了解数学归纳法的原理，能用数学归纳法证明一些简单的数学命题．

三. 教学重点、难点：

重点：合情推理、演绎推理以及证明方法——直接证明和间接证明；

难点：对数学归纳法的理解

四. 知识分析：

【本章知识结构】

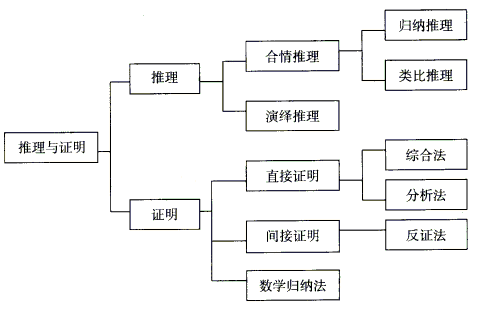
【重点知识回顾】

1、合情推理

前提为真时，结论可能为真的推理，叫做合情推理．

说明：归纳推理和类比推理是数学中常用的合情推理。

（l）归纳推理

根据一类事物的部分对象具有某种性质，推出这类事物的所有对象都具有这种性质的推理，叫做归纳推理（简称归纳）．归纳是从特殊到一般的过程．

说明：归纳推理的前提与结论只具有偶然性联系，其结论不一定正确．结论的正确性还需要理论证明或实践检验．

其一般步骤为：

①通过观察个别情况发现某些相同性质；

②从已知的相同性质中推出一个明确表述的一般性命题（猜想）。

（2）类比推理

根据两类不同事物之间具有某些类似（或一致）性，推测其中一类事物具有与另一类事物类似（或相同）的性质的推理，叫做类比推理（简称类比）。

说明：在一般情况下，如果类比的相似性越多，相似的性质与推测的性质之间越相关，那么类比得出的命题就越可靠．

类比推理的一般步骤为：

①找出两类事物之间的相似性或一致性；

②用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）。

2、演绎推理

根据一般性的真命题（或逻辑规则）导出特殊性命题为真的推理，叫做演绎推理．

演绎推理的特征是：当前提为真时，结论必然为真．例如，由真命题a,b，遵循演绎推理规则得出命题q，则q必然为真．

3、合情推理与演绎推理的区别

归纳和类比是常用的合情推理．从推理形式上看，归纳是由部分到整体，个别到一般的推理，类比是由特殊到特殊的推理，而演绎推理是由一般到特殊的推理．从推理所得的结论来看，合情推理的结论不一定正确，有待进一步证明；演绎推理在大前提、小前提和推理形式都正确的前提下，得到的结论一定正确．

4、证明

（l）直接证明

直接证明是从命题的条件或结论出发，根据已知的定义、公理、定理，直接推证结论的真实性．常用的直接证明方法有综合法与分析法．

综合法是从已知条件出发，经过逐步的推理，最后达到待证结论．

分析法则是从待证结论出发，一步一步寻求结论成立的充分条件．最后达到题设的已知条件或已被证明的事实．

分析法的特点是：从“未知”看“需知”，逐步靠拢“已知”,其逐步推理，实际上是要寻找它的充分条件，

综合法的特点是：从“已知”看“可知”，逐步推向“未知”，其逐步推理，实际上是寻找它的必要条件．分析法与综合法各有其特点，有些具体的待证命题，用分析法或综合法都可以证明出来，人们往往选择比较简单的一种．

（2）反证法（间接证明）

一般地，由证明转向证明：,t与假设矛盾，或与某个真命题矛盾，从而判定为假，推出q为真的方法，叫做反证法．

5、数学归纳法

（l）数学归纳法：设是一个与自然数相关的命题集合，如果①证明起始命题（或）成立；②在假设成立的前提下，推出也成立，那么可以断定，对一切正整数（或自然数）成立．

（2）数学归纳法的框图表示

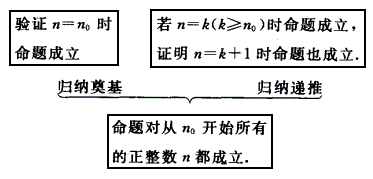
（3）数学归纳法是推理逻辑，它的第一步称为奠基步骤，是论证的基础保证，即通过验证落实传递的起点，这个基础必须真实可靠；它的第二步称为递推步骤，是命题具有后继传递性的保证，即只要命题对某个正整数成立，就能保证该命题对后继正整数都成立，两步合在一起为完全归纳步骤称数学归纳法．这两步各司其职但缺一不可．特别指出的是，第二步不是判断命题的真假，而是证明命题是否具备递推性．如果没有第一步，而仅有第二步成立，命题也可能是假命题．

【专题分析】

一、推理

推理是由一个或几个已知判断作出一个新的判断的思维形式．由于数学中通常把判断称为命题，因而数学推理是由已知命题推出新的命题的思维形式．推理一般分为合情推理和演绎推理，合情推理包括归纳推理和类比推理，演绎推理包括：假言推理、三段论推理、关系推理以及完全归纳推理．

2

1、归纳推理

例1. 在数列中，，，猜想这个数列的通项公式。

解：中，，

所以猜想的通项公式

证明如下：因为，，

所以

即

所以数列

公差为的等差数列

所以

所以通项公式

例2. 在平面上有n条直线，任何两条都不平行，并且任何三条都不交于同一点，问这些直线把平面分成多少部分？

解：设n条直线分平面为部分，先实验观察特例有如下结果：

n与之间的关系不太明显，但－有如下关系：

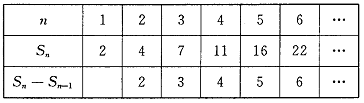
观察上表发现如下规律：－＝n（n＝2，3，…）这是因为在n－1条直线后添加第n条直线被原n－1条直线截得的n段中的任何一段都将它所在的原平面一分为二，相应地增加n部分，所以＝＋n，即－=n，从而－=2，－＝3，－＝4，…，－＝n，将上面各式相加有－＝2＋3＋…＋n，所以＝＋2＋3＋…＋n＝2＋2＋3＋…＋n＝1＋（1＋2＋3＋…＋n）＝

【点评】通过归纳推理得出的结论可能正确，也可能不正确，它的正确性需要通过严格的证明，猜想所得结论即可用演绎推理给出证明，虽然由归纳推理所得出的结论未必是正确的，但它所具有的由特殊到一般、由具体到抽象的认识过程，对于数学的发展、科学的发明是十分有用的。通过观察实验，对有限的资料作归纳整理，提出带有规律性的猜想，也是数学研究的基本方法之一。

归纳推理的一般步骤是：

①通过观察个别情况发现某些相同性质；

②从已知的相同性质中推出一个明确表述的一般性命题（猜想）。

2、类比推理

例3. 著名的欧姆定律就是德国物理学家欧姆在1826年把电传导系统与热传导系统作类比而导出的．电流I与热量Q相当，电压V同温差△T相当，电阻R与比热c的倒数相当．

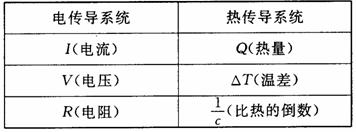
在热传导系统中有关系式：Q=mc△T（m是质量）

于是，就可猜想在电传导系统中有关系式：，这就是欧姆定理．

例4. （1）定义集合A与B的运算：，则

（2）定义集合A与集合B的运算：写出含有集合运算符号“*∪∩”对集合A和B都有的成立的一个等式．

分析：本题是学习——类比——应用新知识的一个题，这就要求同学们能类比课本上学习和研究集合运算的方法，来研究题目中的条件，一般抽象集合问题往往借助于韦恩图求解。

解：（1）由图①中可知AB如图的阴影部分所示，若AB＝C，我们运用类比的方法，可得CA＝B．

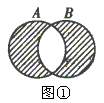
（2）由图②可知，A*B如图阴影部分所示．

运用数形结合，类比的思想方法，结合“*∪∩”符号进行探索，可求得：

或

或等．

3、演绎推理

例5. 在锐角三角形ABC中，AD⊥BC，BE⊥AC，D、E是垂足．

求证：AB的中点M到D、E的距离相等．

分析：解答本题需要利用直角三角形斜边上的中线性质作为大前提．

解：（l）因为有一个内角是直角的三角形是直角三角形 ——大前提

在△ABD中，AD⊥BC。即∠ADB＝90° ——小前提

所以△ABD是直角三角形 ——结论

（2）因为直角三角形斜边上的中线等于斜边的一半 ——大前提

而M是Rt△ABD斜边AB的中点，DM是斜边上的中线 ——小前提

所以 ——结论

同理，所以

【点评】演绎推理的主要形式就是由大前提、小前提推出三段论式推理。三段论推理的依据用集合论的观点来讲就是：若集合M的所有元素都具有性质P，S是M的子集，那么S中所有元素都具有性质P。三段论的公式中包含三个判断：第一个判断称为大前提，它提供了一个一般的原理；第二个判断叫小前提，它指出了一个特殊情况；这两个判断联合起来，揭示了一般原理和特殊情况的内在联系，从而产生了第三个判断——结论。演绎推理是一种必然性推理，它的前提和结论之间有蕴涵关系。因而，只要前提是真实的，推理的形式是正确的，那么结论必定是真实的，但错误的前提可能导致错误的结论。

二、证明

1、综合法证明

综合法是我们在已经储存了大量的知识，积累了丰富的经验的基础上所用的一种方法，其优点是叙述起来简洁、直观、条理、清楚，综合法可使我们从已知的知识中进一步获得新知识．

例6. 由实数构成的集合A满足条件：若，证明：

（1）若，则集合A必有另外两个元素，并求出这两个元素；

（2）非空集合A中至少有三个不同元素。

解：（1）∵

∴

由于－1≠1，有

由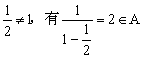

如此循环可知集合A中的另外两个数

（2）∵集合A非空，故存在

∴

即a≠0时，有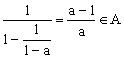

即如此循环出现三个数a，

若，方程无实根

若方程也无实根

若方程无实根

∴a，互不相等，故集合A中至少有三个不同的元素

2、分析法证明

分析法是一种从未知到已知的逻辑推理方法．在探求问题的证明时，它可以帮助我们构思，因而在一般分析问题时，较多地采用分析法，只是找到思路后，往往用综合法加以叙述，正如恩格斯所说“没有分析就没有综合”，在数学证明中不能把分析法和综合法绝对分开．

例7. 若。

解：

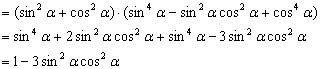
要证

由

∴

∴

3、反证法证明

反证法的理论基础是互为逆否命题的等价性，从逻辑角度看，命题：“若p则q”的否定是“若p则”，由此进行推理，如果发生矛盾，那么就说明“若p则”为假，从而可以导出“若p则q”为真，从而达到证明的目的．反证法是高中数学的一种重要的证明方法，在不等式和立体几何的证明中经常用到，在高考题中也经常出现，它所反映出的“正难则反”的解决问题的思想方法更为重要。

（1）证明否定性、唯一性命题

例8. 求证：两条相交直线有且只有一个交点．

分析：结论中以“有且只有”形式出现，是唯一性命题，常用反证法。

证明：假设结论不成立，即有两种可能：①无交点，②不只有一个交点．

①若直线a、b无交点，那么a//b，与已知矛盾；

②若直线a、b不只有一个交点，则至少有两个交点A和B，这样同时经过点A、B就有两条直线，这与“经过两点有且只有一条直线”相矛盾．

综上所述，两条相交直线有且只有一个交点．

（2）用反证法证明“至多”、“至少”类型问题

例9. 已知a、b、c（0，1），求证：。

证明：假设三式都大于

即 ①

②

③

①×②×③得

又∵

∴ ④

同理 ⑤

⑥

④×⑤×⑥得

矛盾，假设错误，原命题成立。

（3）用反证法证几何问题

例10. 如图所示，AB、CD为圆的两条相交弦，且不全为直径，求证：AB、CD不能互相平分。

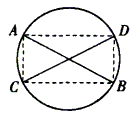
证明：假设AB、CD互相平分，则ACBD为平行四边形

所以∠ACB=∠ADB，∠CAD=∠CBD

因为ABCD为圆内接四边形

所以∠ACB＋∠ADB=180°，∠CAD＋∠CBD=180°

因此∠ACB=90°，∠CAD=90°

所以对角线AB、CD均为直径，与已知矛盾

因此，AB、CD不能互相平分

【点评】（1）反证法的步骤：

①假设命题的结论不成立，即假设结论的反面成立；

②从这个假设出发，经过推理论证，得出矛盾；

③由矛盾判断假设不成立，从而肯定命题的结论成立。

（2）反证法导出结果的几种情况：

①导出非p为真，即与原命题的条件矛盾；

②导出q为真，即与假设“非q为真”矛盾；

③导出一个恒假命题，即与定义、公理、定理矛盾；

④导出自相矛盾的命题。

4、数学归纳法证明

数学归纳法是专门证明与正整数有关的命题的一种方法．它是一种完全归纳法，它的证明共分两步，其中第一步是命题成立的基础，称为“归纳基础”（或称特殊性）．第二步解决的是延续性问题（又称传递性）．运用数学归纳法证明有关命题要注意以下几点：

（1）两个步骤缺一不可；

（2）第二步中，证明“当 n＝k + 1 时结论正确”的过程里，必须利用“归纳假设”即必须用上“当 n＝k 时结论正确”这一结论．

（3）在第二步的证明中，“当 n＝k 时结论正确”这一归纳假设起着已知的作用；“当 n＝k +1 时结论正确”则是求证的目标．在这一步中，一般首先要凑出归纳假设里给出的形式，以便利用归纳假设，然后再去凑出当 n＝k + 1 时的结论．

数学归纳法可以用来证明与正整数有关的代数恒等式、三角恒等式、不等式、整除性问题及几何问题．

（4）不完全归纳法是从特殊出发，通过实验、观察、分析、综合、抽象概括出一般性结论的一种重要方法，运用不完全归纳法可通过对数列前 n 项的计算、观察、分析，推测出它的通项公式或推测出这个数列的有关性质，应明确用不完全归纳去探索数学问题时，必须用数学归纳法对结论的正确性予以证明．

例11. 求证：。

证明：（1）当n=1时，左边，右边，等式成立

（2）假设n=k时，

那么当时，

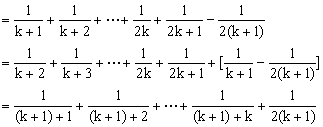
所以时，等式成立

由（1）（2）知对于任何，等式成立

三、归纳、猜想、证明

近年来，高考试题中已出现过这类题型，这类题型是高考的热点之一，它对培养创造性思维具有很好的训练作用．这类题型是：第一步给出命题（与正整数有关）的结构；第二步要求计算出最初的三个至四个初始值；第三步要求通过已计算出的初始值，应用不完全归纳法，发现其命题的一般性规律，作出科学的猜想和判断（要敢于猜想、善于猜想），最后由数学归纳法对所作的猜想——一般性结论，作出完整科学的证明．

例12. 在各项为正的数列中，数列的前n项和满足

（1）求；

（2）由（1）猜想到数列的通项公式，并用数学归纳法证明你的猜想。

解：（1）

∵

∴

得

（2）猜想

证明如下：①n=1时，命题成立；

②假设n=k时，成立

则时

即

∴

∴

即时，命题成立

据①②可知对任意的成立

【模拟试题】

一、选择题（本大题共有12小题，每小题5分，共60分，其中只有一个正确答案。）

1. 我们把平面几何里相似形的概念推广到空间：如果两个几何体大小不一定相等，但形状完全相同，就把它们叫做相似体。下面几何体中，一定属于相似体的是（ ）

①两个球体；②两个长方体；③两个正四面体；④两个正三棱柱；⑤两个正四棱柱

A. ①⑤ B. ②③④ C. ①③ D. ①③⑤

2. （1）已知，求证，用反证法证明时，可假设

（2）已知，求证方程的两根的绝对值都小于1。用反证法证明时可假设方程有一根的绝对值大于或等于1，即假设，以下结论正确的是（ ）

A. （1）与（2）的假设都错误

B. （1）与（2）的假设都正确

C. （1）的假设正确；（2）的假设错误

D. （1）的假设错误；（2）的假设正确

3. 用数学归纳法证明不等式的过程中，由n=k递推到n=k+1时不等式左边（ ）

A. 增加了一项

B. 增加了两项

C. 增加了（B）中两项但减少了一项

D. 以上各种情况均不对

4. 分析法是从要证的不等式出发，寻求使它成立的（ ）

A. 充分条件 B. 必要条件

C. 充要条件 D. 既不充分又不必要条件

5. 用数学归纳法证明：时，第一步即证下述哪个不等式（ ）

A. 1<2 B.

C. D.

6. F(n)是一个关于自然数n的命题，若F(k)真，则真，现已知F（7）不真，则有①F(8)不真；②F(8)为真；③F(6)不真；④F(6)为真；⑤F(5)不真；⑥F(5)真。其中真命题是（ ）

A. ③⑤ B. ①② C. ④⑥ D. ③④

7. 设x、y、z，，则a、b、c三数（ ）

A. 至少有一个不大于2 B. 都小于2

C. 至少有一个不小于2 D. 都大于2

8. 用数学归纳法证明“1＋2＋2²＋……＋2^n－1=2ⁿ－1（）”的过程中，第二步假设n=k时等式成立，则当n=k+1时应得到（ ）

A.

B.

C.

D.

9. 如图1所示，是一个水平摆放的小正方体木块，图2，图3是由这样的小正方体木块叠放而成的，按照这样的规律继续叠放下去，至第七个叠放的图形中，小正方体木块总数应为（ ）

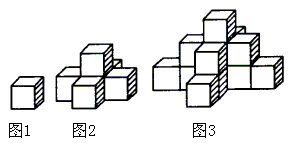
A. 25 B. 66 C. 91 D. 120

10. 类比“两角和与差的正余弦公式”的形式，对于给定的两个函数，，，其中a>0，且a≠1，下面正确的运算公式是（ ）

①；

②；

③；

④；

A. ①③ B. ②④ C. ①④ D. ①②③④

11. 在等差数列中，若，公差d>0，则有，类比上述性质，在等比数列中，若的一个不等关系是（ ）

A. B.

C. D.

12. 已知实数a、b、c满足，abc>0，则的值（ ）

A. 一定是正数 B. 一定是负数

C. 可能是0 D. 正、负不能确定

二、填空题（本大题共4小题，每小题4分，共16分，将答案填在横线上。）

13. （2006·保定）如图，在杨辉三角形中，从上往下数共有n（）行，在这些数中非1的数字之和是____________。

14. 观察下式：，…，则得出结论：____________________________________。

15. 已知数列的前n项和为，且，试归纳猜想出的表达式为________________________。

16. 若记号“※”表示求两个实数a和b的算术平均数的运算，即a※b=，则两边均含有运算符号“※”和“＋”，且对于任意3个实数a、b、c都能成立的一个等式可以是____________________________________。

三、解答题（本大题共6小题，17~21每题12分，第22题14分，每题必须写出必要的解答过程，文字说明。）

17. 已知f(x)对任意实数a,b都有，且当x>0时，。

（1）求证：f(x)是R上的增函数；

（2）f(4)=5，解不等式。

18. 设二次函数中的a、b、c均为整数，且f(0)、f(1)均为奇数，求证：方程f(x)=0无整数根。

19. 在Rt△ABC中，若∠C=90°，则，则在立体几何中，给出四面体性质的猜想。

20. 求证：。（）

21. 若不等式对一切大于1的自然数n都成立，求自然数m的最大值。

22. 已知数列中，（a为常数），是的前n项和，且的等差中项。

（1）求；

（2）猜想的表达式，并用数学归纳法加以证明。

【试题答案】

1. C（只有①③是相似体。）

2. D（对（2）的结论：“两根绝对值都小于1”的否定是“两根绝对值不都小于1”。）

3. B

4. A

5. C

∵且n>1，∴n的初始值为，此时原不等式即为。

6. A

“”等价于“F(k+1)假F(k)假”，故应选A。

7. C（，因此a、b、c至少有一个不小于2，故选C。）

8. D（当n=k时，等式为。那么当n=k+1时，左边=1＋2＋，因此只需在归纳假设两端同时添加，即1＋2＋2²＋……＋＋。）

9. C（。）

10. D（将S(x)，C(x)逐个检验。）

11. B

12. B（∵且（由abc>0知a,b,c均不为0）

∴0，

因此。）

13. （所有数字之和除掉1的和

。）

14. （各等式的左边是第n个自然数到第个连续自然数的和，右边是奇数的平方，故得出结论：=

。）

15. （由，∴，∴）

16. a※b＋c=b※a＋c（∵a※b=，b※a=，∴a※b＋c=b※a＋c。）

17. 解：（1）设，由得

∵，∴

∴

∴f(x)为增函数

（2）∵，∴

∴

∴

解得

18. 证明：假设方程f(x)=0有一个整数根k，则

（1）

∵f(0)=c，f(1)=a+b+c均为奇数，则a+b必为偶数

当k为偶数时，令，则必为偶数，与（1）式矛盾；

当k为奇数时，令，则为一奇数与一偶数乘积，必为偶数，也与（1）式矛盾。

综上可知方程f(x)=0无整数根

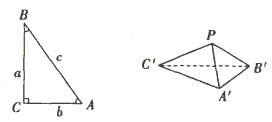
19. 解：如图，在Rt△ABC中

于是把结论类比到四面体中，我们猜想，三棱锥中，若三个侧面两两互相垂直，且分别与底面所成的角为α、β、，则

。

20. 证明：（1）当n=2时，右边，不等式成立。

（2）假设当n=k（）时命题成立，即

则当时，

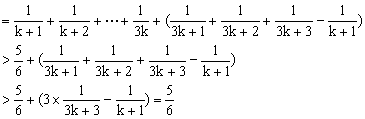
所以当时不等式也成立

由（1），（2）可知，原不等式对一切均成立。

21. 解：设，则

∴n=2时，f(n)有最小值

由，得m<14

∴m的最大值为13

22. 解：（1）

（2）猜想

证明：①当n=1时，左边，右边

∴当n=1时等式成立；当n=2时，左边，右边

∴当n=2时等式成立

②假设当n=k（）时，等式成立，

即，则当时，

∴

∵

∴，将代入，得

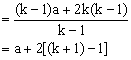
∴当n=k+1时，等式也成立

由①②可知，对于任意的正整数n，等式恒成立

【励志故事】

毛毛虫过河

有一道脑筋急转弯题：一条毛毛虫要到河对岸去，可是没有桥，没有船，毛毛虫怎样过去呢？答案出人意料，却又在情理之中：毛毛虫变成了蝴蝶，它飞过河去了。做毛毛虫时几乎是绝不可想象的事，变成了蝴蝶，轻而易举地就可以办到了。

　　有没有一些困难在你面前，让你以为自己是绝对无法克服的？少一些怨天尤人，少一些悲观失望，耐心地等待时机，想办法充实自己提高自己。困难就好比毛毛虫面前的那条河，当自己从毛毛虫变成蝴蝶时，就可以轻松逾越了。