![]()
【同步教育信息】
一. 本周教学内容:
圆柱和圆锥(一)
[学习过程]
一. 圆柱体的认识
一个长方形以它的一条边为轴旋转一周所形成的几何体就是圆柱体。
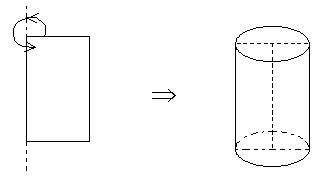
圆柱体上、下两个面是两个大小相等的圆,这两个面是圆柱的底面,围成圆柱的曲面叫做圆柱体的侧面。圆柱体两底面之间的距离叫做圆柱体的高,圆柱体有无数条高。
例1. 一个长方形长8cm,宽6cm,以长边为轴顺时针旋转一周形成一个圆柱体,你能得到这个圆柱体的哪些信息呢?
思路指导:
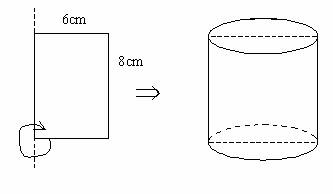
见上图,这个圆柱体的高就是长方形的长(8cm),这个长方形的宽相当于圆柱体的底面半径,所以圆柱体的底面半径是6cm,底面直径是12cm,沿水平方向把圆柱体切成两部分,形成两个小圆柱,这两个小圆柱的底面都相等,两个圆柱的高之和是8cm,水平截面是和底面相等的圆。若沿底面直径纵切成两部分,截面是一个长方形,是一个长12cm,宽8cm的长方形。
想一想:若以宽边为轴逆时针旋转一周呢?
二. 圆柱体的表面积
侧面积:圆柱体的曲面的面积就是圆柱体的侧面积。
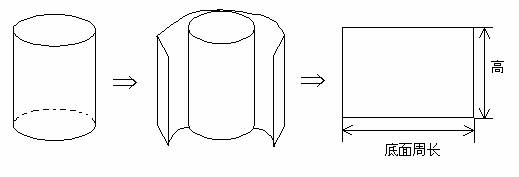
沿着曲面上一条高剪开,圆柱体侧面就转化成一个长方形,当然如果斜着剪开就是一个平行四边形。所以圆柱体侧面展开是长方形或平行四边形,长方形的长相当于圆柱的底面周长,长方形的宽相当于圆柱的高。
所以,圆柱体的侧面积=底面周长×高
![]()
表面积:圆柱体侧面积和上、下两个底面积之和叫做圆柱体表面积。
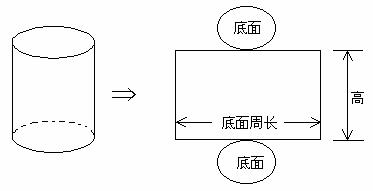
圆柱的表面积=圆柱的侧面积+两个底面的面积
例2. 求下面各圆柱体侧面积或表面积
(1)半径:3厘米,高:7厘米,求S侧=?
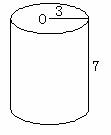
(2)底面直径:2分米,高:3分米,求S表=?
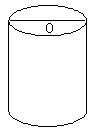
思路指导:(1)圆柱体的侧面积=底面周长×高
通过底面半径先求出底面周长,再用底面周长求高。
![]()
答:该圆柱的侧面积是43.96厘米2。
(2)圆柱体的表面积=侧面积+两个底面面积
侧面积:![]()
底面积:![]()
表面积:![]()
答:该圆柱体的表面积是25.12分米2。
例3. 一个圆柱形汽油桶,底面周长是2.512米,高1.2米,做这样一个汽油桶至少需要多少平方米铁皮?
思路指导:用铁皮做汽油桶,油桶的侧面需用铁皮,上、下两个底面需用铁皮,所以要求至少需要多少铁皮,就是求圆柱的表面积,圆柱的表面积=侧面积+两个底面积。
侧面积:![]()
底面半径:![]()
底面积:![]()
表面积:![]()
答:做这样一个汽油桶至少需要![]() 平方米铁皮。
平方米铁皮。
还可以这样计算圆柱体的表面积:
圆柱体表面积=侧面积+2个底面积
![]()
![]()
利用这个公式解决上面的问题。
![]()

想一想:假如例3做的是一个无盖铁皮水桶,其它条件不变,该怎样解答呢?
三. 圆柱的体积
圆柱所占空间的大小叫做圆柱的体积。
把圆柱体的底面平均分成若干份,再如下图切开,然后拼成一个近似长方体。
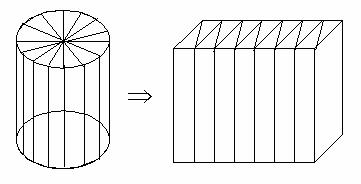
把圆柱体转化成近似的长方体,长方体的体积等于圆柱的体积,长方体的长相当于圆柱底面周长的一半,长方体的宽相当于圆柱底面半径,长方体的底面积相当于圆柱体的底面积,长方体的高相当于圆柱体的高。
因为,长方体体积=底面积×高
![]()
![]()
![]()
所以,圆柱体积 =底面积×高
V = S ×h
例4. 求下面圆柱体的体积(单位:厘米)
(1)![]()
(2)![]()
思路指导:圆柱体积=底面积×高
(1)V=Sh
![]()
答:该圆柱体的体积是62.8立方厘米。
(2)先通过底面周长求出底面积,再乘高。
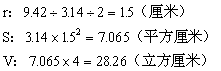
答:该圆柱体的体积是28.26立方厘米。
例5. 求下面立体图形的体积。
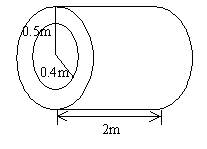
思路指导:这是一个空心圆柱。要求这个空心圆柱的体积,就要先求出大圆柱的体积,再求出里面小圆柱的体积,最后用大圆柱的体积减去里面小圆柱的体积就是空心圆柱的体积。
已知底面外半径是0.5m,内半径0.4m,空心圆柱的高是2m
大圆柱体积:![]()
小圆柱体积:![]()
空心圆柱的体积:![]()
答:这个空心圆柱的体积是0.5652立方米。
也可以这样计算:(列综合算式)
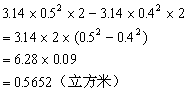
【模拟试题】(答题时间:25分钟)
1. 填空
(1)3.5立方分米=( )立方厘米
1800平方分米=( )平方米
(2)一个边长4厘米的正方形,以它的一条边为轴旋转一周成一个圆柱体,圆柱体的底面周长( )厘米,高是( )厘米。
(3)用一张面积为37平方厘米的长方形纸围成一个圆柱体,这个圆柱体的侧面积是( )平方厘米。
(4)一个圆柱体侧面展开是一个边长9.42分米的正方形,这个圆柱体的底面半径是( )分米。
(5)一个圆柱体侧面积是113.04平方厘米,高是6厘米,体积是( )立方厘米。
2. 求下面圆柱体的侧面积。(单位:厘米)
(1)![]()
(2)![]()
3. 求下面圆柱体的表面积(分米)
(1)![]()
(2)![]()
4. 求下面圆柱的体积。(单位:厘米)
(1)![]()
(2)![]()
(3)![]()
5. 一种铁皮烟囱底面半径5cm,高150cm,制作20节这样的烟囱至少需要铁皮多少平方厘米?
![]()
【试题答案】
1. 填空
(1)3.5立方分米=(3500)立方厘米
1800平方分米=(18)平方米
(2)一个边长4厘米的正方形,以它的一条边为轴旋转一周成一个圆柱体,圆柱体的底面周长(25.12)厘米,高是(4)厘米。
(3)用一张面积为37平方厘米的长方形纸围成一个圆柱体,这个圆柱体的侧面积是(37)平方厘米。
(4)一个圆柱体侧面展开是一个边长9.42分米的正方形,这个圆柱体的底面半径是(1.5)分米。
(5)一个圆柱体侧面积是113.04平方厘米,高是6厘米,体积是(169.56)立方厘米。
2. 求下面圆柱体的侧面积。(单位:厘米)
(1)![]()
17×14=238(平方厘米)
(2)![]()
2×3.14×8×15=753.6(平方厘米)
3. 求下面圆柱体的表面积(分米)
(1)![]()
2×3.14×10×12+2×3.14×102=1381.6(平方分米)
(2)![]()
3.14×6×5+2×3.14×(6÷2)2=150.72(平方分米)
4. 求下面圆柱的体积。(单位:厘米)
(1)![]()
3.14×32×3=84.78(立方厘米)
(2)![]()
3.14×(12÷2)2×10=1130.4(立方厘米)
(3)![]()
50.24÷3.14÷2=8(厘米)
3.14×82×30=6028.8(立方厘米)
5. 一种铁皮烟囱底面半径5cm,高150cm,制作20节这样的烟囱至少需要铁皮多少平方厘米?
2×3.14×5×150×20=94200(平方厘米)
【励志故事】
习惯与自然
一根小小的柱子,一截细细的链子,拴得住一头千斤重的大象,这不荒谬吗?可这荒谬的场景在印度和秦国随处可见。那些驯象人,在大象还是小象的时候,就用一条铁链将它绑在水泥柱或钢柱上,无论小象怎么挣扎都无法挣脱。小象渐渐地习惯了不挣扎,直到长成了大象,可以轻而易举地挣脱链子时,也不挣扎。
驯虎人本来也像驯象人一样成功,他让小虎从小吃素,直到小虎长大。老虎不知肉味,自然不会伤人。驯虎人的致命错误在于他摔了跤之后让老虎舔净他流在地上的血,老虎一舔不可收,终于将驯虎人吃了。
小象是被链子绑住,而大象则是被习惯绑住。虎曾经被习惯绑住,而驯虎人则死于习惯(他已经习惯于他的老虎不吃人)。