【同步教育信息】

一. 本周教学内容：

1. 构成空间几何体的基本元素

2. 棱柱、棱锥和棱台的结构特征

3. 圆柱、圆锥、圆台和球

二. 教学目的

1. 认识构成空间几何体的基本元素

2. 掌握柱、锥、台和球的结构特征

三. 教学重点、难点

1. 柱、锥、台和球的结构特征

2. 学生看图、识图的能力的培养和尝试模型制作

四. 知识分析

我们生活的世界有各种各样的物体，我们总是试着去观察它们，区分它们。区分这些物体的方法很多，但最直接的方法是什么呢？对，是它们占有空间部分的形状和大小。这也是我们研究几何体的方向和内容。

（一）构成空间几何体的基本元素

但是什么是几何体呢？我们将要认识和研究几何体的哪些方面的问题？

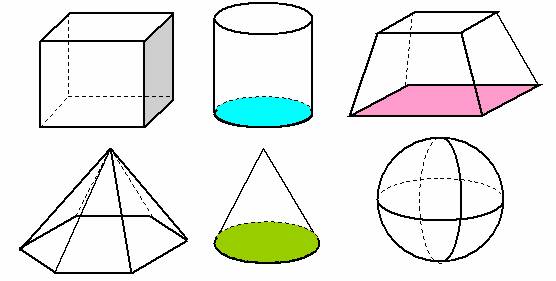几何体指的是一个物体所占有的空间部分。常见的有柱体、锥体、台体、球体等等。（见上图）同学们应该明确一点就是几何体不仅仅包括它的外表面，还包括它内部的部分，或者说它是有皮有瓤的。我们研究几何体，不用理睬它的物理性质和化学成分，不用关心它的历史，也不用研究它的经济价值，而只考虑它的形状和大小，研究一下它的结构特征和构成元素间的逻辑关系等等就行了。

我们现在要学习的内容是立体几何初步，它包括两节内容：第一节是空间几何体，第二节是点、线、面之间的位置关系。学习的重点是认识柱、锥、台、球的结构特征，会用平行投影法、中心投影法、三视图法、直观图法绘制空间图形，柱、锥、台、球等几何体的表面积和体积的求法，平面的基本性质，空间直线的位置关系，直线与平面之间及两平面之间平行和垂直关系，掌握好上述内容，就抓住了立体几何中最重要、最根本的内容，其他部分也就迎刃而解了。

现在，同学们先观察你的周围，发现了哪些几何体？你都认识它们吗？

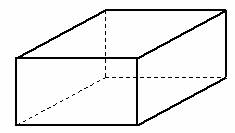
在我们认识的几何体中，最熟悉的莫过于长方体了，你能说出长方体的结构特征吗？观察长方体，会发现它的表面有六个矩形，我们把这六个矩形（含矩形内部）称为长方体的面，相邻两个面的公共边叫做长方体的棱，长方体的三条两两相交成直角的棱交会到一点，就是长方体的顶点。通过观察，我们就可以知道：长方体有8个顶点，12条棱，6个面。长方体通常用长、宽、高来表示它的大小。

其实，所有的几何体都是由点、线、面构成的。点、线、面是构成空间几何体的基本元素，其中线有直线（直线段）和曲线（曲线段）之分，面有平面（或一部分）和曲面（或一部分）之分。

在立体几何中，平面是无限延展的，一个平面可以把整个空间分成两部分，平面是没有厚度的抽象出来的形象。因为平面的无限延展，所以真正的平面画不出来，我们一般是画一个平行四边形表示平面，但有时根据实际情况也有用三角形、五边形、六边形、圆形、椭圆形及各种不规则图形等来表示平面。

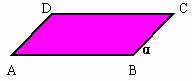
平面一般用希腊字母α、β、γ…表示，还可以用平行四边形的对角（线）顶点表示，如“平面α”、“平面ABCD”，“平面AC”，“平面BD”。

空间中的几何体一方面可以看作是由若干个面（平面的一部分或曲面的一部分）围成的，另一方面也可以用运动的观点来看待：

（1）点动成线：如果点运动的方向始终不变，那么它的轨迹是一条直线或线段，如果点运动的方向时刻在变化，那么它运动的轨迹是一条曲线或曲线的一段。

（2）线动成面：一条线（直线或曲线）运动的轨迹可以是一个面（平面或曲面）。直线平行移动可以生成平面或曲面，直线绕定点转动，可以生成平面或锥面。

（3）面动成体：一个面运动的轨迹（经过的空间部分）可以形成一个几何体。

给出一个几何体，一般我们都可以把它展成平面图形，反之，我们也可以根据所给的平面展开图，还原成相应的几何体。这是这部分内容所涉及的最常见的问题。

（二）多面体和棱柱、棱锥、棱台的结构特征

1. 多面体

多面体是我们接触的相当多的一类几何体，它是由若干个平面多边形（包含它内部的平面部分）围成的。学习时要注意认识多面体的顶点、棱、面，还要注意辨清多面体的体对角线（通常我们称之为多面体的对角线）和面对角线。掌握多面体的几种分类形式。

研究几何体，有时是研究它在某一平面内的性质，这就需要我们把立体问题平面化。除了可以研究几何体的表面，我们还可以研究它的某些个截面（一个几何体与一个平面相交所得的平面图形（包含它的内部））。

2. 棱柱

请同学们想一想，下图中的几何体有哪些共同的几何特征？

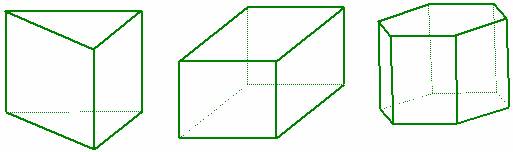
归纳：（1）有两个面是互相平行且全等的多边形。

（2）其余每相邻两个面的交线也互相平行，而这些面也都是平行四边形。

另外，要掌握棱柱的底面、侧面、棱、侧棱、顶点、高和对角线、对角面等概念，掌握棱柱的简单分类。

要辨清直棱柱、斜棱柱、平行六面体、直平行六面体、正四棱柱、长方体和正方体，更要掌握它们之间的联系：

{棱柱}{平行六面体}{直平行六面体}{长方体}{正四棱柱}{正方体}

3. 棱锥

请同学们想一想，下图中的几何体有哪些共同的几何特征？

归纳：（1）有一个面是多边形。

（2）其余各面是有一个公共顶点的三角形。

另外，要掌握棱锥的底面、侧面、棱、侧棱、顶点、高和对角面等概念，掌握棱锥的简单分类。

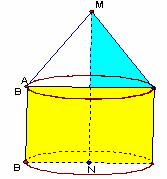
有一种特殊的棱锥，叫做正棱锥。它的特征是：底面是正多边形，并且顶点在底面上的射影是底面的中心。学好正棱锥，关键是掌握它的特征，特别是如图所示的两个直角三角形：由正棱锥的高、棱、底面正多边形外接圆半径构成的直角三角形（浅紫色的三角形）和由正棱锥的高、斜高、底面三角形内切圆半径构成的直角三角形（浅蓝色的三角形）。这是我们在棱锥中经常研究的东西。

4. 棱台

如果一个棱锥被一个平行与底面的平面所截，截面与底面间的部分我们称之为棱台。

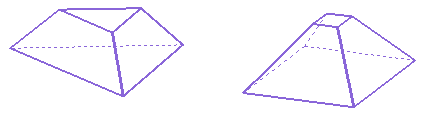
根据棱台的形成，我们就有了判断一个几何体是否是棱台的简单方法：延长棱台的所有的侧棱，如果它们能交于一点，就可以认定这是个棱台，这个方法叫做“还台为锥”。

另外，要掌握棱台的底面、侧面、棱、侧棱、顶点、高和对角面等概念，掌握棱台的简单分类。

也有一种特殊的棱台，叫做正棱台。它的特征是：上下两底面是两个相似的正多边形，并且两底面的中心的连线与两底面垂直。学好正棱台，关键是掌握它的特征，特别是如图所示的两个直角梯形：由正棱台的高、棱、两底面正多边形外接圆半径构成的直角梯形（浅紫色的梯形）和由正棱台的高、斜高、两底面正多边形的内切圆半径构成的直角梯形（浅蓝色的梯形）。这是我们在棱台中经常研究的东西。

（三）圆柱、圆锥、圆台和球

1. 旋转体

请同学们想一想，下图中的几何体有哪些共同的几何特征？

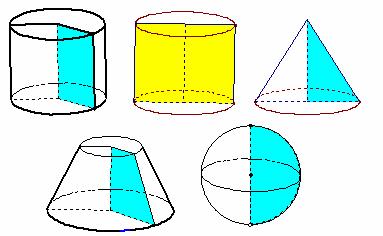
总结：都是由一个平面图形绕着它所在平面内的一条定直线旋转产生的曲面所围成的几何体。

2. 圆柱、圆锥、圆台

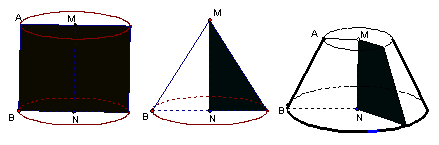
分别以矩形的一边、直角三角形的一直角边、直角梯形垂直于底边的腰所在的直线为旋转轴，其余各边旋转而形成的曲面所围成的几何体分别叫做圆柱、圆锥、圆台。

旋转轴叫做它们的轴，在轴上的这条边（或它的长度）叫做这个几何体的高；垂直于轴的边旋转而成的圆面叫做这个几何体的底面；不垂直于轴的边旋转而成的曲面叫做这个几何体的侧面；无论旋转到什么位置，这条边都叫做侧面的母线。

3. 球和球面

半圆以它的直径为旋转轴，旋转而成的曲面叫做球面。

球面所围成的几何体叫做球体，简称球。

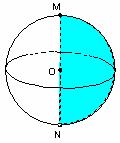
球面可以看作空间中到一个定点的距离等于定长的点的集合，而球就可以看作空间中到一个定点的距离小于或等于定长的点的集合。

用一个平面去截一个球，截面是圆面。如图，球心和截面圆心的连线垂直于截面，球心到截面的距离d与球的半径R及截面的半径r有下面关系：

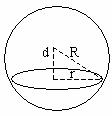
球面被经过球心的平面截得的圆叫做球的大圆；被不经过球心的平面截得的圆叫做球的小圆。

在球面上，两点之间的最短距离，就是经过两点的大圆在这两点间的一段劣弧的长度。我们把这个弧长叫做两点的球面距离。

4. 组合体

由柱、锥、台、球等基本几何体组合而成的几何体叫做组合体。

例如下图中的几何体。

【典型例题】

例1. 根据下图中（左边两个）给出的平面图形，折叠成几何模型，并画出空间图形。

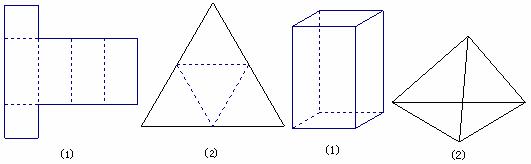
解析：见上图右边两个。

点评：本题通过观察、分析及动手操作，考查了同学们的空间想象力和动手操作能力。

例2. 如图所示，正四棱台AC′的高是17cm，两底面的边长分别是4cm和16cm ,求这个棱台的侧棱长和斜高。

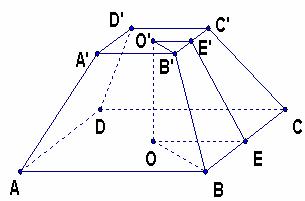
解析：设棱台两底面的中心分别是O′和O，B′C′、BC的中点分别是E′、E，连结O′O、E′E、O′B′、OB、O′E′、OE，则OBB′O′、OEE′O′都是直角梯形。

在正方形ABCD中，BC＝16cm，则OB=cm,OE＝8cm

在正方形A′B′C′D′中，B′C′＝4cm，则O′B′＝cm，O′E′=2cm.

在直角梯形O′OBB′中，

在直角梯形O′OEE′中，

所以，这个棱台的侧棱长为19cm，斜高为。

点评：解决正棱台的相关问题，只要用好那两个直角梯形就可以了。

例3. 把一个圆锥截成圆台，已知圆台的上、下底面半径之比是1∶4，母线长是10cm，求圆锥的母线长。

解析：设圆锥的母线长是ycm，圆台的上、下底面半径分别是x cm、4x cm，作圆锥的轴截面如图所示。

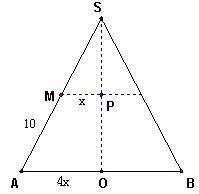
在Rt△SOA中，PM // OA，所以SM∶SA=PM∶OA

即 (y－10)∶y＝x∶4x，解得：

所以，圆锥的母线长为cm。

点评：处理与旋转体有关的问题一般要作出其轴截面，在轴截面中去寻求答案。

例4. 已知半径为5的球的两个平行截面圆的周长分别为6π和8π，求这两个截面间的距离。

解析：设球的轴截面为圆O，AB为球的直径且分别与两个截面交于点C、D，则C、D为截面的圆心，且两圆半径分别为3和4，若两个平行截面在球心同侧，见上图左，则;

若两个平行截面在球心的两侧，见上图右，则，所以两截面间距离为1或7。

点评：解决球及球的截面问题取其大圆，化为圆中问题进行解决。

【模拟试题】

1. 关于平面，下列说法正确的是（ ）

A. 平行四边形是一个平面 B. 平面是有厚薄的

C. 平面是有边界线的 D. 平面是无限延展的

2. 空间三个平面两两相交，将空间最多分成m个部分，最少分成n个部分，则m + n ＝（ ）

A. 5 B. 10 C. 14 D. 16

3. 设M＝{正四棱柱}，N＝{长方体}，P＝{直四棱柱}，Q＝{正方体}，这些集合间的关系是（ ）

A. B.

C. D.

4. 若正棱锥的底面边长与侧棱长相等，则该棱锥一定不是（ ）

A. 三棱锥 B. 四棱锥 C. 五棱锥 D. 六棱锥

5. 四棱台的上、下底面均为正方形，它们的边长分别是2cm和6cm，两底面之间的距离为2cm，则该四棱台的侧棱长为（ ）

A. 3 B. C. D.

6. 长方体三条棱长分别是AA₁=1, AB＝2，AD＝4，则从A点出发，沿长方体的表面到C₁的最短距离是（ ）

A. 5 B. 7 C. D.

7. 一个圆柱的母线长为5，底面半径为2，则圆柱的轴截面的面积为（ ）

A. 10 B. 20 C. 40 D. 15

8. 一个圆锥的母线长为20cm，母线与轴的夹角为30°，则圆锥的高为（ ）

A. cm B. cm C. 20cm D. 10cm

9. 在北纬45°圈上有甲、乙两地，它们的经度分别为东经140°与西经130°，设地球半径为R，则甲、乙两地的球面距离是（ ）

A. B. C. D.

10. 用一个平面去截一个正方体，截面边数最多是____________

11. 正三棱台的上、下底面边长及高分别为1，2，2，则它的斜高是____________

12. 已知长方体的全面积是24，十二条棱长的和为24，则这个长方体一条对角线长是_________

13. 若母线长是4的圆锥的轴截面的面积是8，则圆锥的高是_______________

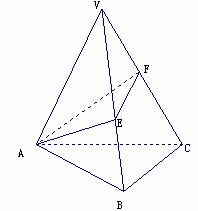
14. 如图，侧棱长为的正三棱锥V－ABC中，∠AVB=∠BVC=∠CVA＝40⁰，过A作截面AEF，求截面三角形AEF周长的最小值。

15. 在半径为25cm的球内有一个截面，它的面积是49πcm²，求球心到这个截面的距离。

【试题答案】

1~9: DCDDCABAD

10. 6 11. 12.

13. 14. 6 15. 24cm

【励志故事】

追求忘我

不要把自己当做鼠，否则肯定被猫吃。

1858年，瑞典的一个富豪人家生下了一个女儿。然而不久，孩子染患了一种无法解释

的瘫痪症，丧失了走路的能力。

　　一次，女孩和家人一起乘船旅行。船长的太太给孩子讲船长有一只天堂鸟，她被这只鸟的描述迷住了，极想亲自看一看。于是保姆把孩子留在甲板上，自己去找船长。孩子耐不住性子等待，她要求船上的服务生立即带她去看天堂鸟。那服务生并不知道她的腿不能走路，而只顾带着她一道去看那只美丽的小鸟。奇迹发生了，孩子因为过度地渴望，竟忘我地拉住服务生的手，慢慢地走了起来。从此，孩子的病便痊愈了。女孩子长大后，又忘我地投入到文学创作中，最后成为第一位荣获诺贝尔文学奖的女性，也就是茜尔玛·拉格萝芙。

　　温馨提示：忘我是走向成功的一条捷径，只有在这种环境中，人才会超越自身的束缚，释放出最大的能量。