反函数的性质及应用

       函数是高中数学中的重要内容，反函数又是函数的重要组成部分，也是同学们学习函数的难点之一。反函数在历年高考中也占有一定的比例。为了帮助同学们更好地掌握反函数相关的内容，对反函数的性质作如下归纳。

       性质1  原函数的定义域、值域分别是反函数的值域、定义域

       在求原函数的反函数及反函数的定义域、值域的有关问题时，如能充分利用这条性质，将对解题有很大帮助。

       例1. 函数的反函数是（    ）。

       A.                                        B.

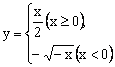C.                                     D.

解析：这是一个分段函数，对分段函数求反函数要注意分段求解。由函数解析式可知当时，；时。由性质1，可知原函数的反函数在时，，则根式前面要有负号，故可排除A、B两项，再比较C、D，易得答案为C。

例2. 若函数为函数的反函数，则的值域为__________。

解析：常规方法是先求出的反函数，再求得的值域为。如利用性质1，的值域即的定义域，可得的值域为。

性质2  若是函数的反函数，则有。

从整个函数图象来考虑，是指与其反函数的图象关于直线对称；从图象上的点来说，是指若原函数过点，则其反函数必过点。反函数中的这条性质，别看貌不惊人，在解题中却有着广泛的应用。

例3. 函数的反函数的图象与轴交于点P（0，2），如下图所示，则方程在[1，4]上的根是（    ）

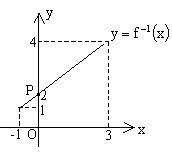
A. 4                             B. 3                             C. 2                             D. 1

解析：利用互为反函数的图象关于直线对称，的图象与轴交于点P（0，2），可得原函数的图象与轴交于点（2，0），即，所以的根为，应选C。

例4. 设函数的图象关于点（1，2）对称，且存在反函数，=0，则=_________。

解析：由=0，可知函数的图象过点（4，0），而点（4，0）关于点（1，2）的对称点为（，4）。由题意知点（，4）也在函数的图象上，即有，根据性质2，可得。

性质3  单调函数一定存在反函数，且反函数与原函数的单调性一致。

在定义域上的单调函数一定存在反函数，但在定义域上非单调函数未必没有反函数，或者说有反函数的原函数不一定是单调函数。如函数有反函数，但其在定义域上不是单调函数。

例5  函数=在区间上存在反函数的充要条件是（    ）

A.                                                B.

C.                                D.

解析：因为二次函数不是定义域内的单调函数，但在其定义域的子区间或上是单调函数，而已知函数在区间上存在反函数，所以或者，即或，应选C。

例6. 已知是定义在R上的单调递增函数，且有，试证明。

证明：（反证法）假设存在，使得。

∵是定义在R上的单调递增函数，

∴由性质3知，也是R上的单调递增函数。

若，则，即，矛盾。同理，当时，也可推出矛盾，故假设不成立，则。

性质4  若是的反函数，则的反函数为，的反函数为。

证明：假设的反函数为，若，则，即，得。

也就是说原函数向左平移a个单位，则反函数向下平移a个单位，其他情况可同理证明。

例7. 设，函数的图象与的图象关于直线对称，求的值。

解析：∵函数的图象与的图象关于直线对称。

∴与互为反函数。

根据性质4，的反函数为。

∴，得。

例8. 设定义域为R的函数、都有反函数，并且函数和的图象关于直线对称，若，求的值。

       解析：由已知条件可知与互为反函数，根据性质4，的反函数为，可得。

∴。