长 春 外 国 语 学 校

        2009—2010学年第二学期第一次月考   高一数学试卷

                 出题人：王先师    审题人：韩敬伟

一、    选择题：（每小题4分，共48分）

1.      某一个几何体的三视图都是等腰三角形，则这个几何体可能是（    ）

A. 圆锥     B. 正四棱锥    C. 正三棱锥    D.正三棱台

2. 如果直线∥，且∥.则与的位置关系是（     ）

   A 相交    B ∥    C.      D ∥或

3. 一个三角形的直观图的面积与其原三角形的面积的比值是（     ）

    A         B  2        C         D

4  一个直角三角形的直角边分别是3与4，以其直角边为旋转轴，旋转而成的

圆锥的侧面积为（    ）

A  15      B  20      C  12      D  15或20

    5. 两个球的表面积之差为48，它们的大圆周长之和为12，则这两个球的

半径之差为（    ）

A  4         B 3         C  2          D  1

    6. 一个圆柱的轴截面为正方形，其体积与一个球的体积之比是3：2，则这个

圆柱的侧面积与这个球的表面积之比为（    ）

A  1:1        B  1:       C  :      D  3:2

    7. 下列四个命题

         （1）与异面，与异面，则与异面

         （2）与相交，与相交，则与相交

    （3）与平行，与平行，则与平行

    （4）与垂直，与垂直，则与垂直

其中真命题的个数为（    ）

A 4           B 3           C 2           D 1

  8. 在正三棱柱ABC—A₁B₁C₁中，若AB=BB₁,则AB₁与C₁B所成的角

的大小是（    ）

A  60⁰            B 90⁰              C 30⁰           D  45⁰

  9. 已知某个几何体的三视图如下，可知这个几何体的体积是（    ）

     A        B       C 4000       D  8000

                

                                                          10

  20

                                                           10

20                         20                          20

正视图                侧视图               俯视图

  10. 已知平面外不共线的三点A,B,C到的距离都相等，则正确的结论是（    ）

      A 平面ABC∥  B平面ABC与相交   C平面ABC与垂直

      D 存在△ABC的一条中位线平行于或在内

  11. ，，下列命题正确的是（    ）

      A 若与相交，则与相交  B若与相交,则

      C 若∥,则与相交        D若∥,则

  12. 不共面的三条定直线，，，若CD=3.则三棱锥

      A—BCD的体积（    ）

      A 随A点的变化而变化         B 随B点的变化而变化

      C 有最大值，无最小值          D 为定值

                         长 春 外 国 语 学 校

      2009—2010学年第二学期第一次月考   高一数学试卷答题卡

一、选择题：（将正确答案填入表格内，每小题4分，共48分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题（每小题4分，共20分）

13. 已知一长方体同一顶点的三条棱长分别为3，4，5，则此长方体的外接球的表面积为______________.                       1

14. 将如右图的直角梯形绕其直腰旋转360⁰，得到

一个_________,其体积为__________.                3

 

                                                         

                                                                                          2

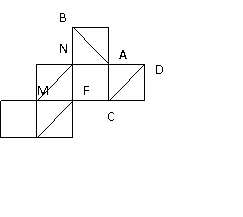          15．已知正四棱锥V—ABCD中，∠AVB=30⁰，VA=cm，蚂蚁从A点出发绕侧面爬行一周，回到A点，最短爬行了___________cm.

          16. 一个正方体展开后如图，则在原正方体中有以下结论：

            （1）AB⊥EF

            （2）AB与CN成60⁰角

            （3）EF与MN是异面直线

            （4）MN∥CD

            其中所有正确命题的序号是___________.

      

          17. 已知是不同的直线，是不重合的平面， 给出下列四个命题：

             （1）若，，，则

             （2）若，，，则

   （3）若，，则

   （4）若异面，，，，，则

     其中所有正确命题的序号是______________.

二、    解答题（每小题13分，共52分）

   18. 一个几何体的三视图如下图所示：

 

 

                                

 

 

                                             

             正视图           侧视图           俯视图 

请你根据所给的三视图求此几何体的表面积与体积。

 

 

 

 

 

 

 

 

 

 

 

 

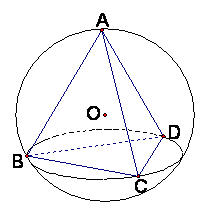
    19. 已知正四面体ABCD内接于求O，正四面体的棱长为，求此正四面体的外接球体积和内切球的表面积。

        

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  20. 已知三棱锥A—BCD，其中E.F分别是AB与CD的中点。且EF=2，

AC=，BD=2，（1）求异面直线AC与BD所成的角；

（2）求异面直线EF与AC所成的角。

 

21. 已知点P为平行四边形ABCD外一点，E, F分别是AB与PC的中点。

 （1）证明：EF∥平面PAD.

 （2）过EF作一截面，使它与平面PAD.平行，并证明你作法的正确性。

     

 

 

 

 

 

长 春 外 国 语 学 校

2009—2010学年第二学期第一次月考 

高一数学答案

一、选择题：（将正确答案填入表格内，每小题4分，共48分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	C	D	C	D	C	A	D	B	B	D	B	D

二、填空题（每小题4分，共20分）

13.      14. 圆台，    15.  6    16. （1）（2）（3）  17. （3）（4）

三、解答题（每小题13分，共52分）

18.    

19.    

20. (1)90⁰  (2) 30⁰

21. 证明（略）