帮你认识对顶角与邻补角

林秀玲

两条直线相交构成四个角，如图1，从位置上把这四个角分为两类，即对顶角与邻补角。学习这两类角，应当注意以下几个方面。

一、掌握两类角的基本特征

对顶角与邻补角是根据它们的位置命名的，因此它们各有不同的特点。

对顶角的特点：有公共顶点，角的两边互为反向延长线。图1中的∠1与∠2、∠3与∠4都是对顶角。对顶角是两个角的位置关系，不是数量关系。

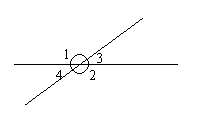
图1

邻补角的特点：有公共顶点和一条公共边，另一边互为反向延长线。图1中的∠1与∠3、∠3与∠2、∠2与∠4、∠4与∠1都互为邻补角。邻补角即是两个角的位置关系，也是数量关系。

对顶角与邻补角都是成对出现的，单独一个角不能称为对顶角或邻补角，这一点大家要注意。例如我们不能说图1中的∠1是对顶角（或邻补角），可以说∠1与∠2是对顶角，∠1是∠3或∠的邻补角。

二、会画一个角的对顶角、邻补角

已知一个角，怎样画出它的对顶角与邻补角呢？其实很简单。反向延长一个角的两边就得到这个角的对顶角，反向延长一个角的任何一边就得到这个角的邻补角。通过画图可知，一个角只有一个对顶角，但一个角有两个邻补角，并且它们是对顶角。

三、掌握两类角的性质

对顶角的性质：对顶角相等。

邻补角的性质：一个角与它的邻补角的和为180°。

同学们要注意邻补角与补角的区别：邻补角一定互补，但互补的两个角不一定是邻补角。因为邻补角即相邻又互补，但互补的两个角不管其位置如何，只要它们的和为180°就是一对互补的角。

四、掌握两类角的两个结论

1、一对对顶角的平分线成一条直线（或互为反向延长线）。

如图2，直线AB与CD相交于点O，OM与ON分别是∠AOD与∠BOC的平分线，则OM、ON成一条直线（或互为反向延长线）。理由如下：

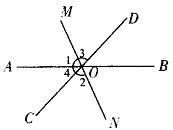
图2

因为OM与ON分别是∠AOD与∠BOC的平分线，所以∠1=∠3=∠AOD，∠2=∠BOC。

由对顶角相等，可得∠AOD=∠BOC，所以∠1=∠2=∠3。

根据平角的定义，可得∠4+∠1+∠3=180°，所以∠4+∠1+∠2=180°，即∠MON是平角，所以OM与ON在一条直线上。

2、一对邻补角的平分线互相垂直。

如图3，∠AOC与∠BOC互为邻补角，OM与ON分别是∠AOC与∠BOC的平分线，则OM⊥ON。理由如下。

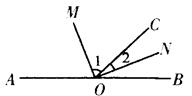
图3

因为OM与ON分别是∠AOC与∠BOC的平分线，所以∠1=∠AOC，∠2=∠BOC。

所以∠1+∠2=（∠AOC+∠BOC）

由邻补角的定义，可得∠AOC+∠BOC=180°

所以∠1+∠2=90°

由垂直的定义可得OM⊥ON。

五、两类角的应用

例1 如图4，三条直线相交于点O，则∠1+∠2+∠3=__________。

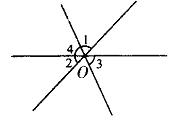
图4

解析：根据对顶角相等，可得∠4=∠3。由平角的定义，可得∠1+∠2+∠4=180°

所以∠1+∠2+∠3=180°

例2 如图5，直线AB与直线CD相交于O点，∠AOC：∠BOC=2：3，求∠BOD的度数。

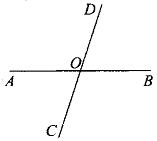
图5

解析：设∠AOC=°，则∠BOC=3x°。

又因为∠AOC与∠BOC互为邻补角，所以。解之得x=36，2x=72。

所以∠AOC=72°

由对顶角相等，得∠BOD=∠AOC=72°。

例3 如图6，直线AB、CD、EF相交于O点，∠AOE=40°，∠BOC=2∠AOC，求∠DOF的度数。

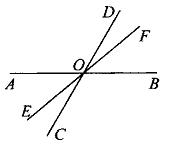
图6

解析：图中∠AOC与∠BOC互为邻补角，结合已知条件∠BOC=2∠AOC，可设∠AOC=x°，则∠BOC=2x°。

由邻补角的定义，可得x+2x=180。解之，得x=60，即∠AOC=60°。

所以∠EOC=∠AOC－∠AOE=60°－40°=20°

由对顶角相等，可得∠DOF=∠EOC=20°