“代数式化简求值”例题解析
代数式化简求值是初中数学教学的一个重点和难点内容。学生在解题时如果找不准解决问题的切入点、方法选取不当,往往事倍功半。如何提高学习效率,顺利渡过难关,笔者就这一问题,进行了归类总结并探讨其解法,供同学们参考。
一. 已知条件不化简,所给代数式化简
例1. (2004年山西省)先化简,再求值:
![]() ,其中a满足:
,其中a满足:![]()
解:![]()
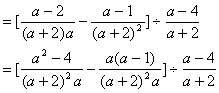
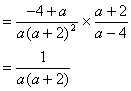
![]()
由已知![]()
可得![]() ,把它代入原式:
,把它代入原式:
所以原式![]()
评析:本题把所给代数式化成最简分式后,若利用![]() ,求出a的值,再代入化简后的分式中,运算过程相当繁琐,并且易错。
,求出a的值,再代入化简后的分式中,运算过程相当繁琐,并且易错。
例2. 已知![]() ,求
,求![]() 的值。
的值。
解:![]()
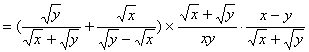
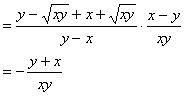
当![]() 时
时
原式![]()
评注:本题属于二次根式混合运算中难度较大的题目。在把所给代数式化简时,首先要弄清运算顺序,其次要正确使用二次根式的性质。
二. 已知条件化简,所给代数式不化简
例3. 已知![]() 为实数,且
为实数,且![]() ,
,![]() ,试求代数式
,试求代数式![]() 的值。
的值。
解:由![]() ,可得:
,可得:
![]()
所以![]()
所以![]()
所以![]()
评注:本题是一道技巧性很强的题目,观察所给已知条件的特点,从已知条件入手,找准解决问题的突破口,化难为易,使解题过程简捷清晰。
三. 已知条件和所给代数式都要化简
例4. (2005年潍坊)若![]() ,则
,则![]() 的值是( )
的值是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
解:因为![]()
所以![]()
所以![]()
所以![]()
所以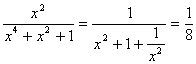
评注:若有![]() ,求出x再代入求
,求出x再代入求![]() 的值将会非常麻烦,但本题运用整体代入的方法,就简单易行。
的值将会非常麻烦,但本题运用整体代入的方法,就简单易行。
例5. 已知![]() ,且满足
,且满足![]() ,求
,求![]() 的值。
的值。
解:因为![]()
所以![]()
所以![]()
所以![]() 或
或![]()
由![]()
故有![]()
所以![]()
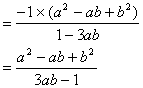
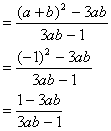
![]()
评注:本题应先对已知条件![]() 进行变换和因式分解,并由
进行变换和因式分解,并由![]() 确定出
确定出![]() ,然后对所给代数式利用立方和公式化简,从而问题迎刃而解。
,然后对所给代数式利用立方和公式化简,从而问题迎刃而解。