绝对值不等式解法指导

黄庆义

带绝对值符号的不等式叫绝对值不等式。解绝对值不等式的关键是去绝对值符号，等价转化为不含绝对值符号的不等式，用已有方法求解。去绝对值符号的方法就是解不等式的方法，有下列四种。

一. 注意绝对值的定义，用公式法

即若，则；若，则或。

例1. 解不等式

解：由题意知，原不等式转化为

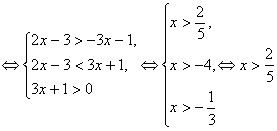
二. 注意绝对值的非负性，用平方法

题目中两边都是非负值才能用平方法，否则不能用平方法，在操作过程中用到。

例2. 解不等式

两边都含绝对值符号，所以都是非负，故可用平方法。

解：原不等式

解得

故原不等式的解集为

三. 注意分类讨论，用零点分段法

不等式的一侧是两个或两个以上的绝对值符号，常用零点法去绝对值并求解。

例3. 解不等式

解：利用绝对值的定义，分段讨论去绝对值符号，令和得分界点

于是，可分区间讨论原不等式

解得

综上不等式的解为

四. 平方法+定义法

有些题目平方之后仍有一个绝对值号，需要用定义去绝对值符号求解，这种方法叫“平方法+定义法”。

例4. 解关于x的不等式

解：化为后，通常分，三种情况去绝对值符号，再分进行讨论，这样做过程冗长，极易出错。改变一下操作程序，思路将十分清晰，过程也简洁得多，即原不等式两边平方得。

再由定义去绝对值号，有：

（1）；

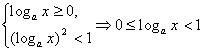（2）。

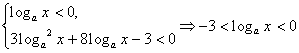综上知

故当时，解为；当时，解为

练一练

1. 已知，且，解不等式。

2. 解不等式

3. 解不等式

答案：1.

2. 解集为

3. 解集为