种群数量增长和数学曲线
种群的数量是指在一定面积或容积中某个种群的个体总数。一个种群的个体数目多少，也叫种群大小。理论上认为，种群大小决定于三个因素：（1）起始种群个体数量；（2）出生和死亡；（3）迁入和迁出。所有能影响种群的出生率、死亡率和迁移率的因素，都会影响种群数量的变化。种群数量的类型有以下几种。
一、种群在无限环境中的指数增长
这样的种群增长模型可以概括为两种：世代不相重叠种群的离散增长模型和世代重叠种群的连续增长模型。
种群在“无限”的环境中，即假定环境中空间、食物等资源是无限的，且气候适宜、没有天敌等理想条件下，种群的增长率不随种群本身的密度而变化，种群数量增长通常呈指数增长。
1. 世代不相重叠种群的离散增长模型
假定某种动物一年只生殖一次，寿命只有一年，那么，这种动物的种群就是世代不相重叠的。例如，草原上往往有季节性的小水坑，栖居在这些小水坑中的水生昆虫，雌虫每年产一次卵，卵孵化长成幼虫，蛹在泥中度过干旱季节，到第二年，蛹才变成虫，并交配、产卵。因此，这样的昆虫种群世代是不重叠的，种群增长是不连续的。对世代不相重叠的种群来说，假定种群增长不受资源、空间等条件的制约，没有迁入和迁出，没有年龄结构，那么，种群的增长就可以用下列方程表示：
其中N0为初始种群数量，t为时间，
为种群的年增长率。
2. 世代重叠种群的连续增长模型
如果种群是世代重叠的，种群的增长则为不间断的连续增长。假定种群的其他特征与上述世代不相重叠的种群相同，种群的瞬时增长率为r，则种群仍表现为指数增长。
大多数种群的繁殖都要延续一段时间并且有世代重叠，即在任何时候，种群中都存在不同年龄的个体。这种情况要以一个连续型种群模型来描述，涉及微分方程。
其积分式为
其中
的定义与世代不相重叠种群增长模型的相同，e=2.71828……，r是种群的相瞬时增长率。
这个公式就是我们所需要的描述连续性变动种群动态的基本模型。这里r代表了种群的瞬时增长率（与密度无关）。如果r>0，种群上升；r=0，种群稳定；r<0，种群下降。用数学曲线表示如下图所示。
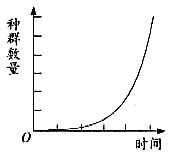
r值能表示物种的潜在增殖能力。例如恒温箱中培养细菌，从一个细菌开始，通过分裂，按2、4、8、16……增长，在短期中能表示出指数增长。许多具简单生活史的动物在实验培养中也具有类似的指数增长。在自然界中，一些一年生昆虫，甚至某些小啮齿类，在春季环境条件较好的情况下，其数量也会呈指数增长。自16世纪以来，世界人口表现为指数增长，所以一些学者称之为人口爆炸。
二、种群在有限环境中的逻辑斯谛增长
种群在有限环境中的增长，同样可以分为世代不相重叠种群增长和连续增长两类。种群在有限环境下的连续增长的一种最简单的形式是逻辑斯谛增长。
因为环境是有限的，大多数种群的指数增长都是暂时的，一般仅发生在早期阶段，种群密度很低，资源丰富的情况下，而随着密度增大，资源缺乏、代谢产物积累等，种群的增长率r势必降低。逻辑斯谛增长模型是建立在以下两个假设基础上的：
①有一个环境容纳量（通常以K表示），当
时，种群为零增长，即
；
②增长率随密度上升而降低的变化是按比例的。最简单的是每增加一个个体，就产生1/K的抑制影响。例如K=100，每增加一个个体，就产生0.01影响，或者说，每一个体利用了1/K的“空间”，N个个体利用了N/K的“空间”，而可供种群继续增长的“剩余空间”只有（1-N/K）。
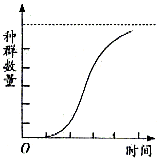
按此两点假设，密度制约导致r随着密度增加而降低，这与r保持不变的非密度制约型的情况相反，种群增长将不再是“J”型，而是“S”型（如下图所示）。“S”型曲线有两个特殊：①曲线渐近于K值，即平衡密度；②曲线上升是平滑的。产生“S”型曲线的最简单数学模型是在指数增长方程（
）上增加一个密度制约因子（
），就得到生态学上著名的逻辑斯谛方程。
在种群增长早期，逻辑斯谛增长与指数增长相差不多，种群数目N很小，N/K也很小，因此（1-N/K）接近于1，所以密度抑制效应可以忽略不计。但随着种群密度增大，密度抑制效应增加，直到当N=K时，种群就停止增长，种群达到了一个稳定的大小不变的平衡状态。
逻辑斯谛曲线常划分为五个时期：①开始期，也可称潜伏期，种群个体数很少，密度增长缓慢；②加速期，随着个体数增加，密度增长逐渐加快；③转折期，当个体数达到饱和密度一半（即K/2）时，密度增长最快；④减速期，个体数超过K/2以后，密度增长逐渐变慢；⑤饱和期，种群个体数达到K值而饱和。
逻辑斯谛模型的两个参数r和K，均具有重要的生物学意义。R表示物种的潜在增殖能力；K是环境容纳量，即物种在特定环境中的平衡密度。但应注意，K同其他生态学特征一样，也是随环境（资源量）的改变而改变的。
逻辑斯谛增长模型的重要意义：①它是许多两个相互作用种群增长模型的基础；②它也是渔业、林业、农业等实践领域中，确定最大持续产量的主要模型；③模型中两个参数r、K，已成为生物进化理论中的重要概念。