等效场模型

江苏 吴俊

【题源示例】如图1所示，两个水平放置的带电平行金属板的匀强电场中，一长为l的绝缘细线一端固定在O点，另一端拴着一个质量为m、带有一定电量的小球，小球原来静止，当给小球某一速度后，它可绕O点在竖直平面内做匀速圆周运动，若两板间电压增大为原来的4倍时，求：

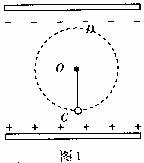
（1）要使小球从C点开始在竖直平面内做圆周运动，开始至少要给小球多大速度？

（2）在运动过程中细线所受的最大拉力。

分析解答：本题的物理情景不难想象：一绳系带电小球在两板间原来的电场中做匀速圆周运动。后来两板间电压升高为4倍，小球仍在竖直面内做圆周运动。这两种情况下相应的物理条件是不同的，必须注意正确地把它们转化为具体的物理条件。

（1）设原来两极板间电压为U，间距为d，小球电量为q，因小球开始能在电场中做匀速圆周运动，故小球所受电场力向上，并且和重力相等，所以小球带正电，且满足

①

当两板间电压增到4U时，设需在C点给小球的速度为v才能使其在竖直平面内做圆周运动，分析知C点就是小球做圆周运动的等效最高点（即临界点），在等效最高点处小球的线速度最小，小球所受新的电场力与重力的合力恰好满足在该处做圆周运动的向心力，此时细线对小球的拉力为零（这是等效最高点的特点），即：

②

得到

（2）小球在最高点D时就是小球做圆周运动的等效最低点，小球在等效最低点处的线速度最大，所以细线L所受拉力最大，设拉力为T，由牛顿第二定律，有：

④

小球C点运动到D点过程中，重力和电场力做功，根据动能定理，有：

⑤

由⑤式得小球在等效最低点处的线速度

⑥

将⑥式代入④式，得。

点悟：物体仅在重力场中运动是最简单，也是学生最为熟悉的运动类型，但是物体在复合场中的运动又是我们在综合性试题中经常遇到的问题，如果我们能化“复合场”为“等效重力场”，不仅能起到“柳暗花明”的效果，同时也是一种物理思想的体现，如何实现这一思想方法呢？请看模型特征。

【模型特征】物体在重力场中，最低点对应最低的等高线，物体在最低点为超重状态；最高点对应最高的等高线，最高点要看是绳件还是杆件，物体在不同的点之间可以用牛顿运动定律或能量守恒定律列式。

如物体在恒力场中，我们可以先求出合力F，F为物体处于平衡位置时的合力，再根据求出等效场的加速度，将物体的运动转化为我们熟悉的直线运动、曲线运动（抛体或圆周运动），直线运动利用牛顿运动定律或功能角度都可以解题，曲线运动一般利用功能角度解答。

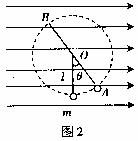
如图2所示，空间有水平向右的匀强电场，电场强度为E，小球质量为m，带电量为+q被长为l的轻绳固定在O点，此时小球受重力和电场力，平衡位置A偏离竖直位置角，在同一直径上另一点为B，物体受到合力为，类比重力场中运动，相当于“等效重力加速度”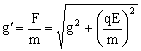，A为“最低点”，B为“最高点”，故小球能在竖直平面内做完整的圆周运动的条件是，小球通过B点时的速度，然后应用能量关系可以求出在图示竖直位置最低点应具有的最小速度。

从以上分析可知等效分析时关键是类比得出此时的等效重力加速度和临界位置、临界条件。

【易错警示】在应用公式时要注意g与g′的区别：对于竖直平面内的圆周运动模型，则要从受力情形出发，分清“地理最高点”和“物理最高点”，弄清有几个场力；竖直平面内若做匀速圆周运动，则必须根据做匀速圆周运动的条件，找出隐含条件；同时还要注意线和导轨类问题的约束条件的不同。

【题源激变】

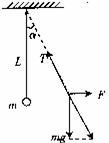
背景：一个质量为m的带正电的小球在匀强电场中，沿图示方向运动，场强方向是水平的。	背景：一质量为m的小球用长为L的细线悬挂在天花板上，现加一大小恒定的水平向右的风力后，小球的悬线摆动时偏离竖直方向的最大偏角为	背景：如图所示，半径为R的光滑绝缘导轨固定于竖直平面内，加上某一方向的匀强电场时，带正电的小球沿轨道内侧做圆周运动，在A点时小球对轨道的压力为N，此时小球的动能最大。
问题：求小球运动到最高点时其电势能与在O点的电势能之差？	问题：试求风力的大小？类比电场中的场强，“风力场强”为多少	问题：若小球的最大动能比最小动能多W，且小球能够到达轨道上的任意一点（不计空气阻力），则：小球的最小动能是多少？小球受到重力和电场力的合力是多少？