![]()
【本讲教育信息】
一. 教学内容:
暑假专题——三角函数的图象和性质
二、本周教学目标:
(1)会用单位圆中的三角函数线画出正弦函数y=sinx,正切函数y=tanx的图象,并在此基础上根据诱导公式画出余弦函数y=cosx的图象;理解周期函数的定义。并通过它们的图象理解并掌握正弦函数y=sinx,余弦函数y=cosx,正切函数y=tanx的性质。
(2)会用“五点法”画出正弦函数y=sinx、余弦函数y=cosx、函数y=Asin(ωx+![]() )的简图,并理解A、
)的简图,并理解A、![]() 、
、![]() 的物理意义。
的物理意义。
(3)会根据y=sinx的基本性质,讨论y=Asin(ωx+![]() )的性质。
)的性质。
三、本周知识要点:
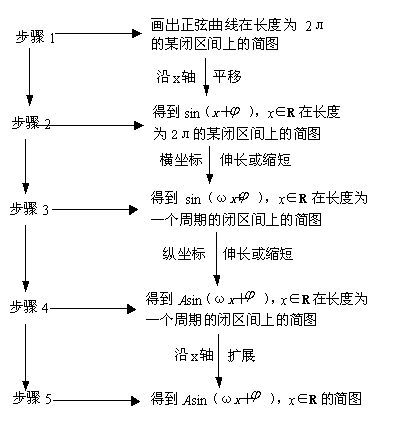
(一)知识系统及其结构:
![]()

(二)基本概念及相关知识点:
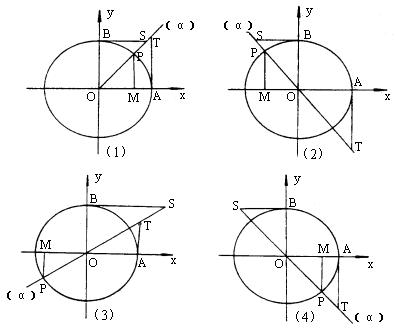
1、三角函数线:
设单位圆圆心在原点,和横坐标的正方向OX交于A点,与角α的终边交于P点,从P点作OX的垂线MP,垂足为M。
sinα=MP(正弦线),cosα=OM(余弦线),tanα=AT(正切线)。
有向线段MP,OM,AT,统称三角函数线。
2、三角函数图象的作法:
(1)几何法:利用单位圆中的三角函数线,作出各三角函数的图象,以正弦函数为例,具体作法如下:
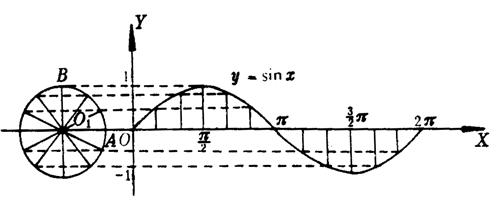
在直角坐标系的x轴上任取一点O1,以O1为圆心作单位圆,从这个圆与x轴的交点A起把圆分成12等份。过圆上的各分点作x轴的垂线,可以得到对应于角0,![]() ,
,![]() ,
,![]() ,…,2π的正弦线。相应地,再把x轴上从0到2π这一段(2π≈6.28)分成12等份.把角x的正弦线向右平移,使得正弦线的起点在x轴上,再用光滑曲线把这些正弦线的终点连结起来,就得到了正弦函数y=sinx(x∈[0,2π])的图象。
,…,2π的正弦线。相应地,再把x轴上从0到2π这一段(2π≈6.28)分成12等份.把角x的正弦线向右平移,使得正弦线的起点在x轴上,再用光滑曲线把这些正弦线的终点连结起来,就得到了正弦函数y=sinx(x∈[0,2π])的图象。
(2)描点法及其特例——五点作图法
三角函数的图象亦可用通常作函数图象的描点法作出。对于正弦函数及余弦函数可用五点法作出简图。
(3)利用图象变换作三角函数图象。
三角函数的图象变换有振幅变换、周期变换和相位变换等。
由y=sinx的图象上的点的横坐标保持不变,纵坐标伸长(当A>1)或缩短(当0<A<1=到原来的A(A>0且A≠1)倍,得到y=sinx的图象,叫做振幅变换或叫沿y轴的伸缩变换。
由y=sinx的图象上的点的纵坐标保持不变,横坐标伸长(0<ω<1=或缩短(ω>1)到原来的![]() (ω>0且ω≠1)倍,得到y=sinx的图象,叫做周期变换或叫做沿x轴的伸缩变换。
(ω>0且ω≠1)倍,得到y=sinx的图象,叫做周期变换或叫做沿x轴的伸缩变换。
由y=sinx的图象上所有的点向左(当φ>0)或向右(当φ<0=平行移动|φ|个单位,得到y=sin(x+φ)的图象,叫做相应变换或叫做沿x轴方向的平移。
由y=sinx的图象上所有的点向上(当b>0)或向下(当b<0=平行移动|b|个单位,得到y=sinx+b的图象叫做沿y轴方向的平移。
由y=sinx的图象变换到y=Asinx(ωx+φ)的图象,需要同时运用振幅变换、周期变换及相位变换,将由专门条目介绍。
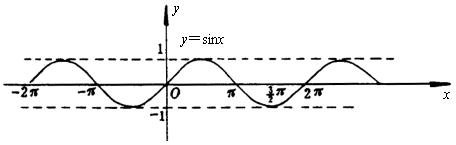
3、三角函数的图象:
三角函数的图象从“形”的侧面反映了三角函数随自变量x变化而变化的规律,使抽象的三角函数性质转化为直观形象的图象。
y=sinx
y=cosx
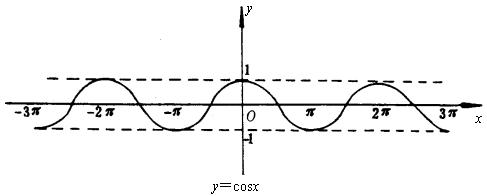
y=tanx
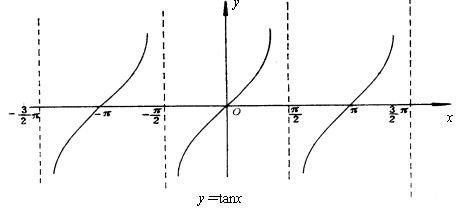
4、正弦函数的主要性质:
(1)定义域是实数集R,记作y=sinx,x∈R
(2)值域是[-1,1],当且仅当x=![]() +2k
+2k![]() ,k∈Z时取得最大值1,当且仅当x= -
,k∈Z时取得最大值1,当且仅当x= -![]() +2k
+2k![]() ,k∈Z时取得最小值-1;
,k∈Z时取得最小值-1;
(3)周期性:正弦函数是周期函数,2k![]() (k∈Z,且k≠0)是它的周期,最小正周期是2
(k∈Z,且k≠0)是它的周期,最小正周期是2![]() ;
;
(4)奇偶性:正弦函数是奇函数;
(5)单调性:正弦函数在每一个闭区间[-![]() +2k
+2k![]() ,
,![]() +2k
+2k![]() ](k∈Z)上都是增函数,其值从-1增大到1;在每一个闭区间[
](k∈Z)上都是增函数,其值从-1增大到1;在每一个闭区间[![]() +2k
+2k![]() ,
,![]() +2k
+2k![]() ](k∈Z)上都是减函数,其值从1减小到-1。
](k∈Z)上都是减函数,其值从1减小到-1。
5、余弦函数的主要性质:
(1)定义域是实数集R,记作y=cosx,x∈R;
(2)值域是[-1,1],当且仅当x=2k![]() ,k∈Z时取得最大值,当且仅当x=(2k+1)
,k∈Z时取得最大值,当且仅当x=(2k+1)![]() ,k∈Z时取得最小值-1;
,k∈Z时取得最小值-1;
(3)余弦函数是周期函数,2k![]() (k∈Z,且k≠0)是它的周期,最小正周期是2
(k∈Z,且k≠0)是它的周期,最小正周期是2![]() ;
;
(4)奇偶性:余弦函数是偶函数.
(5)单调性:余弦函数在每一个闭区间[(2k-1)![]() ,2k
,2k![]() ](k∈Z)上都是增函数,其值从-1增加到1;在每一个闭区间[2k
](k∈Z)上都是增函数,其值从-1增加到1;在每一个闭区间[2k![]() ,(2k
,(2k![]() +1)](k∈Z)上都是减函数,其值从1减小到-1。
+1)](k∈Z)上都是减函数,其值从1减小到-1。
6、正切函数的主要性质:
(1)定义域是{x|x≠![]() +k
+k![]() ,k∈Z}
,k∈Z}
(2)值域是实数集R
(3)周期性:正切函数是周期函数,周期是![]()
(4)奇偶性:正切函数是奇函数
(5)单调性:正切函数在开区间(-![]() +k
+k![]() ,
,![]() +k
+k![]() ),k∈Z内都是增函数。
),k∈Z内都是增函数。
补充:正弦函数是以2π为最小正周期的周期函数,每一条直线![]() 都是正弦曲线的一条对称轴;每一个点(kπ,0)都是正弦曲线的一个对称中心。
都是正弦曲线的一条对称轴;每一个点(kπ,0)都是正弦曲线的一个对称中心。
余弦函数是以2π为最小正周期的周期函数,每一条直线![]() 都是余弦曲线的一条对称轴;每一个点
都是余弦曲线的一条对称轴;每一个点![]() 都是余弦曲线的一个对称中心。
都是余弦曲线的一个对称中心。
7、周期函数:对于函数y=f(x),如果存在一个不为零的常数T,使得当x取定义域内的每一值时,f(x+T)=f(x)都成立,那么就把函数y=f(x)叫做周期函数。非零常数T叫做这个函数的周期.周期函数的周期不只一个,若T是周期,则2T,3T,-T…,都是周期,如果所有周期中存在一个最小正数,这个最小正数,叫做函数f(x)的最小正周期。
8、函数y=Asin(ωx+φ)的图象:
当函数y=Asin(ωx+φ)(A>0,ω>0),x∈[0,+∞]表示一个振动量时,A就表示这个量振动时离开平衡位置的最大距离,通常把它叫做振动的振幅;往往振动一次所需要的时间T=![]() ,叫做振动的周期;单位时间内往复振动的次数f=
,叫做振动的周期;单位时间内往复振动的次数f=![]() =
=![]() ,叫做振动的频率;ωx+φ叫做相位,φ叫做初相(即当x=0时的相位)。
,叫做振动的频率;ωx+φ叫做相位,φ叫做初相(即当x=0时的相位)。
一般地,函数y=Asin(ωx+φ)(A>0,ω>0)(x∈R)的图象可以看作用下面的方法得到:先把y=sinx的图象上的所有的点向左(φ>0)或向右(φ<0)平移|φ|个单位,再把所得各点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的![]() 倍(纵坐标不变),再把所得各点的纵坐标伸长(A>1)或缩短(0<A<1=到原来的A倍(横坐标不变)。
倍(纵坐标不变),再把所得各点的纵坐标伸长(A>1)或缩短(0<A<1=到原来的A倍(横坐标不变)。
若是先压缩后平移,此时平移的量为![]() 个单位。
个单位。
说明:三角函数的图象的掌握体现在:把握图象的主要特征(顶点、零点、中心、对称轴、单调性、渐近线等);应当熟练掌握用“五点法”作图的基本原理以及快速、准确地作图。
【典型例题】
例1. 利用单位圆中的三角函数线证明:
当![]() 时,
时,![]() 。
。
证明:任取![]() ,分别作出角x的正弦线CD及正切线AT。(见图01)
,分别作出角x的正弦线CD及正切线AT。(见图01)
根据S△OAD<S扇形OAD<S△OAT,
即:![]() ,
,
化简整理即得:![]() 。
。
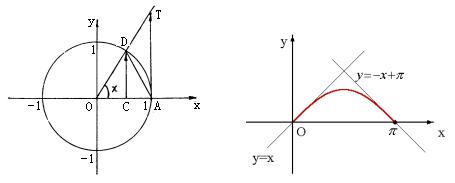
图01 图02
引伸:![]() 时,
时,![]() 的几何意义是:函数y = sin x的图象位于直线y = x
的几何意义是:函数y = sin x的图象位于直线y = x
的下方。(见图02)。
依据图形的对称性,我们不难得到:
当![]() 时,y = sin x的图象位于直线:y = -x+π的下方。
时,y = sin x的图象位于直线:y = -x+π的下方。
例2. 求函数![]() x∈R的单调递增区间。
x∈R的单调递增区间。
解:令![]() ,函数y =-2 sin t的单调递增区间是函数y = sin t的单调递减区间。
,函数y =-2 sin t的单调递增区间是函数y = sin t的单调递减区间。
由![]() ,即
,即![]() ,
,
解得:![]()
![]()
∴所求的单调递增区间是![]()
![]() 。
。
例3. 选择题
要得到函数![]() 的图象,可以将函数y = 3 sin2 x的图象( )
的图象,可以将函数y = 3 sin2 x的图象( )
A. 沿x轴向左平移![]() 单位 B. 沿x轴向右平移
单位 B. 沿x轴向右平移![]() 单位
单位
C. 沿x轴向左平移![]() 单位 D. 沿x轴向右平移
单位 D. 沿x轴向右平移![]() 单位
单位
分析:我们知道,当a>0时,把函数y = f (x)的图象沿x轴向右移a个单位,便得到函数y = f (x-a)的图象,把函数f (x)的图象沿x轴向左平移a个单位,便得到函数y = f (x+a)的图象。本题中![]() 与y = 3 sin 2x的对应法则不同,应当把它们变为“y = f (x)与y = f (x+a)”的形式后,再讨论平移关系。因为我们关心的是对函数y = 3 sin 2x的图象平移,所以要把
与y = 3 sin 2x的对应法则不同,应当把它们变为“y = f (x)与y = f (x+a)”的形式后,再讨论平移关系。因为我们关心的是对函数y = 3 sin 2x的图象平移,所以要把![]() 变形,变到y = 3 sin (2x+φ)的形式。
变形,变到y = 3 sin (2x+φ)的形式。
由正弦曲线和余弦曲线的关系,不难看出,把余弦曲线沿x轴向右平移![]() ,就得到正弦曲线,即是
,就得到正弦曲线,即是![]() (这与诱导公式的结论是一致的)。利用这个关系,可以得到:
(这与诱导公式的结论是一致的)。利用这个关系,可以得到:
![]()
![]()
问题成为:把函数y = 3 sin 2x的图象沿x轴进行怎样的平移,可以得到函数
![]() 的图象?
的图象?
如果y =
3 sin 2x = f (x),那么![]()
![]()
![]() 。可见,把函数y = 3 sin 2x的图象向左移
。可见,把函数y = 3 sin 2x的图象向左移![]() 个单位后,可得到函数
个单位后,可得到函数![]() 的图象,即得到函数
的图象,即得到函数![]() 的图象,因此选A。
的图象,因此选A。
【模拟试题】(答题时间:45分钟)
一、选择题:
1. 四个函数① y = sin x,② y =-cos x,③ y = tan x,④ y = -cot x中,在区间
(0,π)上是增函数的有( )
A. 1个 B. 2个 C. 3个 D. 4个
2. 将函数y = sin x的图象向左平移![]() 个单位,再把(平移后的)的图象上每个点的横坐标缩小为原来的
个单位,再把(平移后的)的图象上每个点的横坐标缩小为原来的![]() (纵坐标不变),得到的图象的函数解析式为( )
(纵坐标不变),得到的图象的函数解析式为( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
3. 函数![]() 的一个增区间是( )
的一个增区间是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
二、填空题:
4. 函数![]() 是最小正周期为
的函数。
是最小正周期为
的函数。
5. 在△ABC中,如果tan A · tan B>1,则△ABC的形状是 。
三、解答题:
6. 设函数f (x) = 3+m cos x的值域为[-2,8],如果tan m>0,求实数m的值。
7. 求函数![]() 的定义域。
的定义域。
8. 设函数f (x) = sin (ωx+φ) (![]() ),给出以下四个论断:
),给出以下四个论断:
① 它的图象关于直线![]() 对称;
对称;
② 它的图象关于点![]() 对称;
对称;
③ 它的周期是π;
④ 它在区间![]() 上是增函数。
上是增函数。
以其中的两个论断作为条件,余下的两个论断作为结论,写出正确的两个命题,并对其中的一个命题加以证明。
![]()
【试题答案】
一、选择题
1. B 2. B 3. C
二、填空题
4. ![]() 5、锐角三角形
5、锐角三角形
三、解答题
6. m = 5
① ②
7. 提示:要使函数有意义,当且仅当:
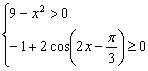
![]()
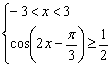
解②得: ![]() ≤
≤![]() ≤
≤![]() ,
,![]()
利用数轴找①、②的公共部分为:![]() <
<![]() ≤
≤![]() 或
或![]() ≤
≤![]() ≤
≤![]() ,即函数的定义域为
,即函数的定义域为
{![]()
![]() <
<![]() ≤
≤![]() 或
或![]() ≤
≤![]() ≤
≤![]() }。
}。
8. 提示:两个正确命题为①、③![]() ②、④和②、③
②、④和②、③![]() ①、④ 证明前一个命题:
①、④ 证明前一个命题:
由③知:ω = 2, ∴ f (x) = sin (2x+φ)
由①知:![]()
∵![]() <
<![]() ∴
∴ ![]() 从而f (x) = sin (2x+
从而f (x) = sin (2x+![]() )
)
这样便不难检验②、④成立了。