![]()
【本讲教育信息】
一. 教学内容:
①单位圆中的三角函数线与三角函数作图
②正弦函数的图像与性质;
③余弦函数的图像与性质;
④正切函数的图像与性质
二、学习目标
1、能利用单位圆中的三角函数线解决一些简单的问题,如判断三角函数的符号、比较三角函数值的大小等;
2、借助单位圆中的三角函数线画出![]()
![]() ,
,![]() 的图像,了解三角函数的周期性。
的图像,了解三角函数的周期性。
3、借助图像理解正弦函数、余弦函数在![]() 上,正切函数在
上,正切函数在![]() 上的性质(如单调性、最大值和最小值、图像与
上的性质(如单调性、最大值和最小值、图像与![]() 轴交点等)。
轴交点等)。
三、知识要点
1、三角函数线
如图,设角α的终边与单位圆的交点为P,过P作x轴的垂线,垂足为M;又设单位圆与x轴正半轴交点为A,过点A作x轴的垂线交角α的终边或其反向延长线于T。
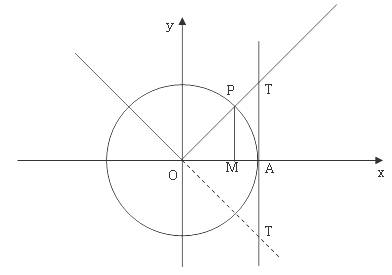
根据正弦,余弦,正切的定义,则有![]() ,
,![]() ,
,![]()
这三条与单位圆有关的有向线段![]() 分别叫做角
分别叫做角![]() 的正弦线,余弦线,正切线.
的正弦线,余弦线,正切线.
【说明】(1)符号的判断:当MP、OM、AT的方向与相应的坐标轴正方向一致的时候,取正值;相反时取负值;比如,当α为第一象限角时,MP的方向与y轴正向一致,故对应的sinα>0;
(2)当角![]() 的终边落在
的终边落在![]() 轴上时,
轴上时,![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合,此时正弦线,正切线分别变成一个点;当角
重合,此时正弦线,正切线分别变成一个点;当角![]() 的终边在
的终边在![]() 轴上时,
轴上时,![]() 与
与![]() 重合,余弦线变成一个点,过
重合,余弦线变成一个点,过![]() 的切线平行于
的切线平行于![]() 轴,不能与角
轴,不能与角![]() 的终边相交,所以正切线不存在,此时角
的终边相交,所以正切线不存在,此时角![]() 的正切值不存在.
的正切值不存在.
2、三角函数线与诱导公式
设α、β的终边分别与单位圆交于P、P',则β=α+π+2kπ
由三角函数的定义可知:
sinα=MP,sinβ=M'P'
因为MP与M'P'长度一致而方向相反,故:sinα=-sinβ即:sin(π+2kπ+α)=-sinα
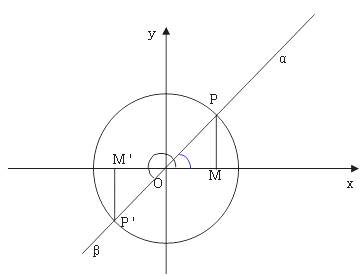
【说明】其它各个诱导公式均可根据三角函数线进行推导和理解。
3、三角函数线与三角函数作图
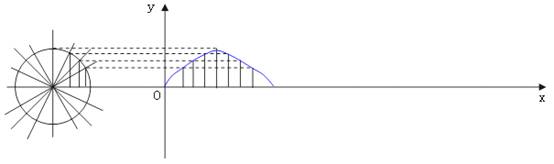
1)通过三角函数线平移作正弦和正切函数图像
基本作法是:将三角函数线平移到坐标系中相应的位置,然后将其端点用一条光滑的曲线连接起来即得到相应三角函数的图像。(下图是(0,π)上正弦函数图像的作图过程)。
2)余弦函数的图像可由正弦函数的图像向左平移![]() 个单位而得到。
个单位而得到。
3)三角函数的图像
正弦函数的图像:定义域R,值域[-1,1];
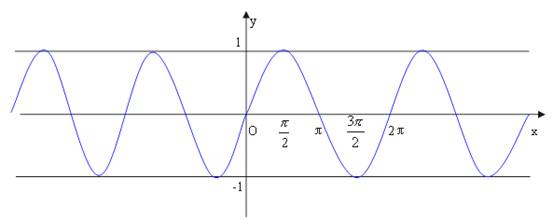
‚余弦函数的图像:定义域R,值域[-1,1];
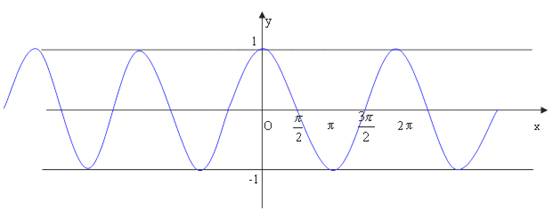
ƒ正切函数的图像:定义域![]() ,值域R。
,值域R。
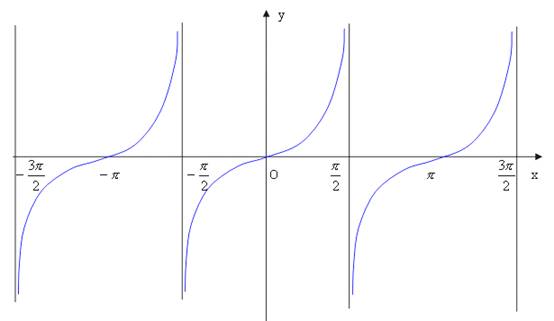
4、三角函数的有界性
|sinx|∈[0,1],|cosx|∈[0,1];
‚在定义域内的某个闭区间上,正余弦及正切函数均为有界函数
5、三角函数的周期性
正余弦函数的周期为2π,2kπ(k∈Z)均为其周期;
正切函数的周期为π,kπ(k∈Z)均为其周期;
6、三角函数的奇偶性
正弦函数y=sinx(x∈R),正切函数y=tanx(x∈![]() )均为奇函数;余弦函数y=cosx(x∈R)为偶函数
)均为奇函数;余弦函数y=cosx(x∈R)为偶函数
7、三角函数的单调性
正弦函数的单调增区间:![]()
正弦函数的单调减区间:![]() ;
;
余弦函数的单调增区间:![]() ;
;
余弦函数的单调减区间:![]() ;
;
正切函数的单调增区间:![]()
8、三角函数的对称性
正弦函数图像的对称轴:![]() ;对称中心:(kπ,0),k∈Z;
;对称中心:(kπ,0),k∈Z;
余弦函数图像的对称轴:![]() ;对称中心:
;对称中心:![]() ;
;
正切函数图像的对称中心:![]()
四、考点解析与典型例题
考点一 三角函数线的应用
例1、已知x为锐角,试比较![]() 的大小。
的大小。
【分析】需根据三角函数线,将比较对象转换成可度量的量(线段)进行比较。
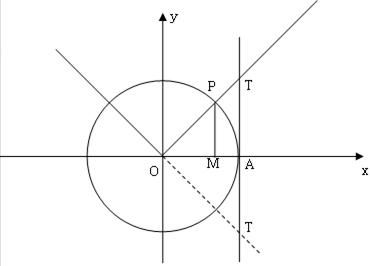
【解】记锐角x的终边与单位圆的交点为P,作其正弦线MP和正切线AT如图:
由三角函数线的意义可知:
sinx=MP,tanx=AT,x=![]() .
.
由于MP<AP<![]() <AT,故三者之间的大小关系为:
<AT,故三者之间的大小关系为:![]() 。
。
考点二 求三角函数的定义域
例2、求下列函数的定义域:![]() ;‚
;‚![]()
【解】由题意得
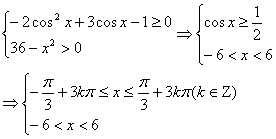
取k=-1,0,1,可得
![]()
即所求定义域为
![]() 。
。
‚由题意得
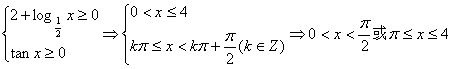
即函数的定义域为![]() 。
。
考点三 求三角函数的值域及最值
例3、求函数![]() 的最小值。
的最小值。
【分析】求三角函数式的值域或最值的基本策略是将三角函数式化为“一个角,一个三角函数”,然后采取配方法,利用三角函数的有界性求解;‚字母![]() 的取值范围不明确,故求该函数的最值必须采取分类讨论的策略
的取值范围不明确,故求该函数的最值必须采取分类讨论的策略
【解】配方得:![]()
故:![]() ;‚
;‚![]() ;ƒ
;ƒ![]()
考点四 三角函数的单调性
例4、求函数![]() 的单调区间。
的单调区间。
【分析】整体处理:先以![]() 为一个整体,求出其所在区间,然后再解出
为一个整体,求出其所在区间,然后再解出![]() 所在区间。
所在区间。
【解】因为![]() 时为单调增函数,故函数
时为单调增函数,故函数![]() 的单调增区间满足:
的单调增区间满足:![]() ,从而解得原函数的单调区间为:
,从而解得原函数的单调区间为:![]()
考点五 求函数的奇偶性
例5、判断下列函数的奇偶性:![]() ;‚
;‚![]() 。
。
【分析】判断奇偶性首先应判断定义域关于原点的对称性,然后再由奇偶性的定义进行判断。
【解】定义域为R,关于原点对称。又:
![]() 故知其为偶函数。
故知其为偶函数。
‚由![]() ,定义域关于原点对称。因为
,定义域关于原点对称。因为![]() ,故其为奇函数。
,故其为奇函数。
考点六 三角函数的对称性
例6、作出函数![]() 的图像。
的图像。
【分析】可先作出![]() 的图像,再利用对称性作图。
的图像,再利用对称性作图。
【解】
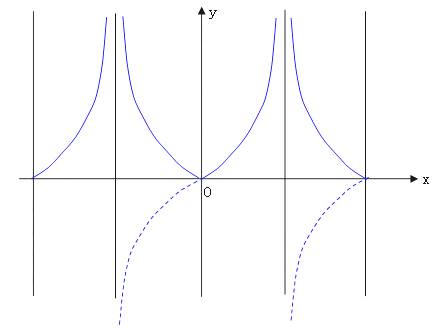
五、数学思想方法
本讲主要结合三角函数图像研究函数性质,学习中要注意数形结合的思想方法的应用;另外,对于正切函数以及含有参变量的函数的研究要注意分类讨论的思想方法的应用,准确把握引起分类讨论的因素,从而准确分类,要做到“不重不漏”即把要讨论的变量在整个取值范围内进行区间划分,不能有所遗漏,所划分的区间的交集为空集,不能有所重叠。
【模拟试题】(答题时间:80分钟)
一、选择题
1、设![]() ,
,![]() ,
,![]() ,则
,则
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、已知cos(α-![]() )+sinα=
)+sinα=![]()
A、-![]() B、
B、![]() C、-
C、-![]() D、
D、![]()
3、下列函数中,周期为![]() 的是
的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、已知![]() ,那么角
,那么角![]() 是
是
A.第一或第二象限角 B.第二或第三象限角
C.第三或第四象限角 D.第一或第四象限角
5、函数![]() 的图象
的图象
A.关于点![]() 对称 B.关于直线
对称 B.关于直线![]() 对称
对称
C.关于点![]() 对称 D.关于直线
对称 D.关于直线![]() 对称
对称
6、函数![]() 的一个单调增区间是
的一个单调增区间是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
*7、已知偶函数y=f(x)在[-1,0]上为单调递减函数,又![]() 、
、![]() 为锐角三角形的两内角,则
为锐角三角形的两内角,则
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题
*8、函数![]() 的定义域为______________________________。
的定义域为______________________________。
*9、已知函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,则函数
,则函数![]() 的最小正周期为_____________,值域为_________________.
的最小正周期为_____________,值域为_________________.
三、解答题
10、画出函数![]() 的图像。
的图像。
11、比较大小(1)sin110°,sin150°;(2)tan220°,tan200°;(3)![]() ;
;
(4)![]()
12、设![]() ,求
,求![]() 的最大值与最小值。
的最大值与最小值。
13、解不等式![]() .
.
![]()
【试题答案】
一、选择题
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
答案 |
D |
C |
D |
C |
A |
C |
A |
偶函数在[-1,0]上为减函数,故在[0,1]上为增函数,因为
α+β>![]()
二、填空题
![]() ;
;
【分析】
![]()
![]() 。
。
9、![]()
![]() ;
;
【分析】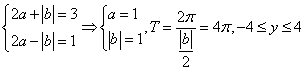
三、解答题
10、解:将函数![]() 的图像关于
的图像关于![]() 轴对称,得函数
轴对称,得函数![]()
的图像,再将函数![]() 的图像向上平移一个单位即可。
的图像向上平移一个单位即可。
11、(1)sin110°=sin70°,sin150°=sin30°,而sin70°>sin30°,∴sin110°>sin150°
(2)tan220°=tan40°,tan200°=tan20°,而tan40°>tan20°,∴tan220°>tan200°
(3)![]() ; (4)
; (4)![]() 。
。
12、![]() ,而
,而![]() 是
是![]() 的递减区间
的递减区间
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 。
。
13、因为对任意![]() ,
,![]() ,所以原不等式等价于
,所以原不等式等价于![]() .
.
即![]() ,
,![]() ,
,![]() ,故解为
,故解为![]() .
.
所以原不等式的解集为![]() .
.