![]()
【本讲教育信息】
一、教学内容
数据的收集、频率与频数(5.1-5.3)
二、教学目标:
1. 了解普查、抽样调查、总体、样本、个体、频率、频数这些基本概念。
2. 会求一组数据的频率和频数。
3. 会绘制频数分布直方图与频数分布折线图。
三、知识要点分析:
1. 调查
(1)为了一定的目的而对考察对象进行的全面调查,称为普查,其中所要考察对象的全体称为总体,而组成总体的每一个考察对象称为个体。
(2)从总体中抽取部分个体进行调查,这种调查称为抽样调查,其中从总体中抽取的一部分个体叫做总体的一个样本。
(3)在调查过程中选择普查还是抽样调查的主要依据:若要求全面了解数据,且总体个数较少时,采用普查的方式;而若总体中个体数目较多,调查时具有危险性、破坏性或受客观条件的限制,采用抽样调查。抽样时要注意样本的代表性和广泛性。
2. 频数与频率
(1)频数:在统计中,每个对象出现的次数叫做频数。
(2)频率:每个对象出现的次数与总次数的比值叫做频率。
(3)频数分布表:将数据适当分组,得到相应各组所考查的对应的个数,制成表格即为频数分布表。
(4)频数分布直方图:依据频数分布表绘制出各个小组与其相应的考察对象个数关系的图形,即为频数分布直方图。
(5)频数分布折线图:为了更好地刻画数据的总体规律,在得到的频数分布图上取点(每个条形块顶部正中)连线,即可得到相应的频数分布折线图。
【典型例题】
知识点1:数据的收集
例1. 指出下列调查是适用于普查,还是适用于抽样调查:
(1)调查除夕之夜我国有多少人观看中央电视台第一频道的春节晚会;
(2)调查某工厂生产的一万件胶卷中有无不合格产品;
(3)调查一万张面值为100的人民币中有无假币;
(4)调查当今中学生中,喜欢听年轻教师讲课的多,还是喜欢听年老教师讲课的多。
题意分析:题目给出了四项调查,判断这四项调查适用于普查,还是适用于抽样调查。
思路分析:(1)中要调查的人数太多,适用于抽样调查;(2)中的调查可能带有破坏性,应进行抽样调查;(3)中假币的危害大,调查一万张百元人民币工作量也不大,应进行普查;(4)中调查的学生较多,工作量较大,适用于抽样调查。
解:这四项调查中,只有(3)应以普查的方式进行,其余三项均应以抽样调查的方式进行。
解题后的思考:一般来讲,当要求全面了解数据,且总体个数较少时,采用普查的方式。但受各种条件的影响,抽样调查也是非常必要的。
例2. 某商店为了考察10000筐梨的等次,从中抽取了50筐进行检查,下面说法正确的是( )
A. 总体是10000筐梨
B. 总体是10000筐梨的等次
C. 个体是每筐梨
D. 样本是50筐梨
题意分析:本题考察的是梨的等次,而不是梨.
思路分析:本题中,总体是全部10000筐梨的等次,个体是每筐梨的等次,样本容量是抽取考察对象的个数。故应选B。
解:B
解题后的思考:在区别具体问题中的总体、个体、样本时,首先要明确所考察的对象是什么。
例3. 小明、小亮和小丽想要了解他们所生活的小区里小朋友的年龄情况,小明调查了当天在院子里玩耍的小朋友,情况如图①所示;小亮调查了他所居住的二单元的小朋友,情况如图②所示;小丽调查了每个单元一楼的两家住户中小朋友的年龄,数据如下(单位:岁):3、16、14、15、17、8、4、6、9、7、17、12、2、13、6、5、12、14、3、15、5、16、1、1。

这个小区中小朋友的年龄情况到底如何?你认为谁的调查方式好一些,为什么?如果你去调查的话,你有没有更好的方式?
题意分析:本题要求判断小明、小亮、小丽三个人的调查方式哪一个好,还有没有比他们更好的方式。
思路分析:小明的调查范围只在当天院子里玩耍的小朋友,一般不具有代表性;小亮的调查范围只在二单元的小朋友,调查的对象较少,不具有广泛性;一般认为小丽的调查范围较好。
解:小丽的调查方式好一些,因为小丽的调查具有代表性、广泛性,自己的调查方式略。
解题后的思考:抽样调查时一般应注意:被调查对象不得太少,被调查对象应是随机抽取的,调查数据应是真实的等。
小结:普查可以直接获得总体的情况。但有时总体中个体数目较多,普查的工作量较大;有时受客观条件的限制,无法对所有个体进行普查;有时调查具有破坏性,不允许普查。抽样调查只考察总体中的一部分个体,因此它的优点是调查范围小,节省时间、人力、物力和财力,但其调查结果往往不如普查得到的结果准确。为了获得较为准确的调查结果,抽样时要注意样本的代表性和广泛性。
知识点2:频率与频数
例4. 为了参加学校年级之间的广播体操比赛,八年级准备从63名学生中挑出身高相差不多的40名学生参加比赛,为此收集到这63名同学的身高(单位:cm)数据如下:
158、158、160、168、159、159、151、158、159
168、158、154、158、154、169、158、158、158
159、167、170、153、160、160、159、159、160
149、163、163、162、172、161、153、156、162
162、163、157、162、162、161、157、157、164
155、156、165、166、156、154、166、164、165
156、157、153、165、159、157、155、164、156
选身高在哪个范围的学生参加呢?画出频数分布直方图和折线图。
题意分析:把这63个身高数据进行整理,画出频数分布直方图,根据频数分布情况选出40个相差不多的数据。
思路分析:首先求出这组数据的最大值和最小值的差,决定组距和组数,列出频数分布表,然后再画频数分布直方图和折线图。
解:因为这组数据的最大值是172,最小值是149,所以172-149=23,数据分成8组,组距为3,制成频数分布表:

画出频数分布直方图:要选出40名身高相差不多的同学参加比赛,从155≤x<164这三个区域内选择最合适,其中有41名,去掉一个最大的就可以。折线图如下:
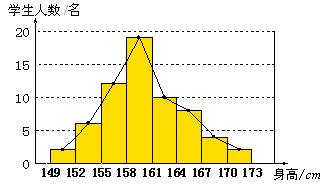
解题后的思考:在确定组数和组距时,并不唯一,只要合理,能直观形象地反映数据的分布情况即可。在列频数分布表时可采用唱票法进行累计,注意不要遗漏或重复累计,在绘制频数分布折线图时,可以在所绘得的频数分布直方图上取点、连线,也可直接绘制频数分布折线图,注意所取的点应在“条形”或所取组距上部的正中,这样可使得所绘制的频数分布折线图更为直观地反映频数的分布情况,否则整个图形就可能向左或向右偏移,产生一定的视觉偏差。
例5. 对某班学生一次数学成绩进行统计分析,各分数段的人数如图所示(分数取正整数),请观察图形,回答下列问题:
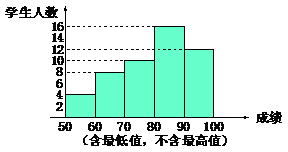
(1)该班有多少名学生?
(2)80~90这一组的频数、频率分别是多少?
(3)估计该班这次测验的平均成绩。
题意分析:本题给出了频数分布直方图,要求根据直方图回答问题。
思路分析:该班总人数等于各分数段人数之和,80~90这一组的频数是16,其频数除以总数即为频率。
解:(1)4+8+10+16+12=50。
(2)80~90这一组的频数为16,频率为16÷50=0.32。
(3)取每组的中间值为该组的平均成绩,则可估计该班这次测验的平均成绩=(4×55+8×65+10×75+16×85+12×95)÷50=79.8。
解题后的思考:首先要理解频数和频率的本质含义,通过频数分布直方图读出数据进行有关计算。
例6. 为了增强学生的身体素质,某校坚持长年的体育锻炼,并定期进行体能测试,下面是某班学生的立定跳远成绩(精确到0.01m),整理后分成5组,画出的频数分布直方图的一部分;已知从左到右4个小组的频率分别是0.05,0.15,0.30,0.35。第5小组的频数是9。

(1)请将频数分布直方图补充完整;
(2)该班参加这次测试的学生有多少人?
(3)若成绩在2.00m以上(含2.00m)为合格,该班成绩的合格率是多少?
(4)在这次测试中,你能肯定该班学生成绩的众数和中位数各落在哪一小组内吗?(只需写出能或不能,不必说明理由)。
题意分析:本题要求先补全频数分布直方图,再根据直方图计算参加测试的学生人数、成绩的合格率等。
思路分析:要补全频数分布直方图,必须计算出第5小组条形块的高度,前4个小组的频率分别是0.05,0.15,0.30,0.35,所以第5个小组的频率为1-0.05-0.15-0.30-0.35=0.15,可见第5小组和第2小组高度相同。
解:(1)1-0.05-0.15-0.30-0.35=0.15,补充的频数分布直方图如图所示:

(2)因为第5小组的频率为0.15,频数为9,所以该班参加这次测试的学生人数为9÷0.15=60(人)。
(3)因为第三、四、五各小组的频率之和为0.80,所以该班成绩的合格率为80%。
(4)不能肯定众数、中位数各在哪一小组内。
解题后的思考:绘制频数分布直方图要利用小长方形的高与频率成正比这一性质去确定各小长方形的高。
小结:根据频数分布表,可看到数据在各范围内的分布情况,哪个范围内数据最多或最少、占数据的百分比等。根据频数分布表还可以说明“频数之和=1”,由频数分布直方图中还看到小长方形的高和频率成正比例。
总结:本节课主要学习了数据的收集和数据的频数分布。本节课涉及到的概念较多,不必死记硬背,理解其基本含义即可。主要包括:总体、个体、样本、样本容量,普查、抽样调查、频数、频率、频数分布直方图等。还涉及到了一个非常重要的数学思想,即用样本估计总体的思想。
【预习导学】
(数据的波动(5.4))
一、预习前知
刻画数据“平均水平”的量度有哪几个?
二、预习导学
1. 一组数据中的最大数据与最小数据的差在统计学中叫做__________。
2. 方差是各个数据与平均数之差的平方和的平均数,即s2=__________。
3. 一组数据的极差、方差或标准差越小,这组数据就越__________。
4. 已知一组数据1、2、1、0、-1、-2、0、-1,则这组数据的平均数是__________,极差是__________,方差是__________。
反思:(1)刻画数据“波动状况”的量度有哪几个?
(2)如何计算一组数据的方差和标准差?
【模拟试题】(答题时间:50分钟)
一、选择题
1. 为了检查一批零件的长度,从中抽取50个进行检测,在这个问题中,个体是( )
A. 零件的长度的全体
B. 每一个零件
C. 每个零件的长度
D. 50个零件
2. 下列调查中,适宜采用全面调查(普查)方式的是( )
A. 调查一批新型节能灯泡的使用寿命
B. 调查长江流域的水污染情况
C. 调查重庆市初中学生的视力情况
D. 为保证“神舟7号”的成功发射,对其零部件进行检查
3. 要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是( )
A. 调查全体女生
B. 调查全体男生
C. 调查九年级全体学生
D. 调查七、八、九年级各100名学生
4. 在抽样调查时,样本应具有:①代表性;②特殊性;③广泛性;④典型性。其中正确的个数有( )
A. 1个
B. 2个
C. 3个
D. 4个
5. 要了解某地区10万九年级毕业生的数学中考成绩的情况,随机抽取人数较合适的是( )
A. 1人
B. 10人
C. 2000人
D. 5万人
6. 某校测量了九年级(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如图所示频数分布直方图,则下列说法正确的是( )
A. 该班人数最多的身高段的学生数为7人
B. 该班身高低于160.5cm的学生数为15人
C. 该班身高最高段的学生数为20人
D. 该班身高最高段的学生数为7人

7. 某中学有125名教师,将他们的年龄分为6组,在38~45岁这组内有25人,那么这一组的频率是( )
A.
5
B.
0.2
C. 0.32
D. 0.24
*8. 八年级(4)班选举班长,通过投票最后统计三名候选人A、B、C的票数比为6∶3∶1,已知该班共有50人且每人的选票中只填A、B、C三人中的某1人,则候选人B获得的票数的频数为( )
A.
30
B.
15
C. 5
D. 20
二、填空题
1. 为了检验2000支日光灯管的使用寿命,从中抽出10支测量使用寿命,这种调查方式为__________,总体为__________,个体为__________,样本为__________。
2. 为了了解奥运会上运动员的执行情况(对违禁药物服用情况),对运动员进行尿样检查,可采用__________的方法。
3. 对某中学同龄的70名学生的身高进行测量后,得到一组数据,其中最大值为169cm,最小值为146cm,对这组数据进行整理后,确定它的组距为2.3cm,则组数为__________。
4. 在一块试验田抽取1000个麦穗,考察它的长度(单位:cm),对数据适当分组后看到落在5.75~6.05cm之间的频率为0.36,于是估计出在这块田里长度为5.75~6.05cm之间的麦穗约占__________。
5. 为了了解“丰收三轮车”在某地区农村的使用情况,小明对某村使用三轮车的100户农户进行了统计,对于小明的这种做法,你的看法是__________(填“同意”或“不同意”),理由是__________。
6. 对某班50名学生的数学成绩进行统计,90~95分的学生有10名,则这一分数段的频数为__________,频率为__________。
*7. 某市青年排球队12名队员的年龄情况如下表所示:
|
年龄(岁) |
18 |
19 |
20 |
21 |
22 |
|
人数(人) |
1 |
4 |
3 |
2 |
2 |
则这12名队员年龄的最小值是__________,其频数是__________,最大年龄的频率是__________,出现次数最多的年龄的频率是__________。
**8. 把128个数分成8组,已知第一组到第四组的频数分别为10、24、4、26,第五组到第七组的频率分别为0.165、0.125、0.085,那么第八组的频率是__________,频数是__________。
三、解答题
1. 某医院为了了解病人每分钟呼吸次数,对20名病人进行测量,结果记录如下:12、20、16、18、20、28、23、16、15、18、20、24、18、21、18、19、18、31、18、13。
(1)你能说出该医院采用了什么样的调查方式吗?其中总体、个体、样本分别是什么?
(2)你能求出这组数据的平均数、中位数及众数吗?
2. 1936年,美国《文学文摘》杂志根据1000万户电话用户和从该杂志订户所收回的意见,断言兰登将以370∶161的优势在总统竞选中击败对手罗斯福,但结果却是罗斯福当选总统,《文学文摘》大丢面子。
原来,在1936年,能安装电话或订阅《文学文摘》杂志的人,在经济上都相对富裕,与此同时收入不太高的大多数选民却选择了罗斯福。《文学文摘》的教训对你有什么启示呢?
3. 已知一组数据:26、26、24、22、24、26、28、26、28、26、30、22、26、24、28、30、26、26、30、28。
(1)求众数;
(2)求平均数;
(3)分组填写频率分布表。
|
分组 |
频数 |
频率 |
|
21~23 |
|
|
|
23~25 |
|
|
|
25~27 |
|
|
|
27~29 |
|
|
|
29~31 |
|
|
|
合计 |
|
|
(4)画出频数分布直方图。
**4. 某校九年级学生共900人,为了了解这个年级学生的体能,从中随机抽取部分学生进行1min的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理,下图是这四名同学提供的部分信息:
甲:将全体测试数据分成6组绘成频数分布直方图(如图);
乙:跳绳次数不少于106次的同学占96%;
丙:第①、②两组频率之和为0.12,且第②组与第⑥组频数都是12;
丁:第②、③、④组的频数之比为4∶17∶15。
根据这四名同学提供的材料,请解答如下问题:
(1)这次跳绳测试共抽取多少名学生?各组有多少人?
(2)如果跳绳次数不少于135次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为多少?
(3)以每组的组中值(每组的中点对应的数据)作为这组跳绳次数的代表,估计这批学生1min跳绳次数的平均值。

![]()
【试题答案】
一、选择题
1. C 2. D 3. D 4. B 5. C
6. D【图中小长方形的高代表学生人数,不代表学生的身高】
7. B【25÷125=0.2】
![]()
二、填空题
1. 抽样调查,2000支日光灯管的使用寿命,每支日光灯管的使用寿命,所抽出的10支日光灯管的使用寿命
2. 普查 3. 10 4.
36% 5. 不同意,他的抽样不具有广泛性和代表性
6. 10, 7. 18,1,0.167,0.333
8. 0.125,16【第一组到第四组的频数之和为:10+24+4+26=64,频率之和为:64÷128=0.5。第五组到第七组的频率之和为:0.165+0.125+0.085=0.375。频数之和为:0.375×128=48。所以第八组的频率为1-0.5-0.375=0.125,频数为:128-64-48=16。】
三、解答题
1. (1)抽样调查。总体:某医院全体病人每分钟呼吸次数。个体:每位病人每分钟呼吸次数。样本:20名病人每分钟呼吸的次数。(2)将已知20个数据从小到大排列得12、13、15、16、16、18、18、18、18、18、18、19、20、20、20、21、23、24、28、31。≈19,中位数为(18+18)÷2=18,众数为18。
2. 通过这段文字我们发现《文学文摘》在抽样调查时,没有关注样本的代表性和广泛性,故调查结果不准确。从中得出的启示是:在抽取样本时,既要注重样本的大小,又要注重样本的广泛性和代表性,这样才能获得较为准确的调查结果。
3. (1)由于26这个数据出现了8次,次数最多,故众数为26。(2)![]()
(3)如下表所示:
|
分组 |
频数 |
频率 |
|
21~23 |
2 |
0.10 |
|
23~25 |
3 |
0.15 |
|
25~27 |
8 |
0.40 |
|
27~29 |
4 |
0.20 |
|
29~31 |
3 |
0.15 |
|
合计 |
20 |
1.00 |
(4)如图所示:

4. (1)第①组频率为:1-96%=0.04,∴第②组频率为:0.12-0.04=0.08,这次跳绳测试共抽取学生人数为:12÷0.08=150人,∵第②、③、④组的频数之比为4∶17∶15,可算得第①~⑥组的人数分别为6、12、51、45、24、12。
(2)第⑤、⑥两组的频率之和为=0.16+0.08=0.24,由于样本是随机抽取的,估计全年级有900×0.24=216人达到跳绳优秀。
![]()