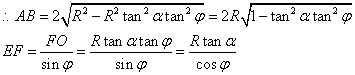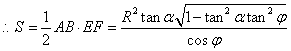【本讲教育信息】

一、教学内容

选修4—1 第二章 圆锥曲线

二、教学目标

1. 使学生了解直线与球的位置关系、平面与球的位置关系的判断方法。

2. 使学生了解正投影和平行投影的概念；

3. 理解平面与圆柱面的截线是椭圆（特殊情形是圆）.理解利用丹迪林（Dandelin）双球证明平面截圆柱、平面截圆锥的截面的类型及其证明方法。

三、教学重、难点

直线与球的位置关系、平面与球的位置关系的判断方法是教学的重点，亦是教学的难点。

四、知识要点分析

1. 直线与球的位置关系：

直线与球心的距离为d，球的半径为R：

若d＞Ｒ，则直线与球相离（无公共点）。ｄ＜Ｒ，直线和球相交（两个公共点），ｄ＝Ｒ，直线和球相切（一个公共点）

空间中，过球外一点可以作无数条直线和球相切，这些切线长都相等，所有的切点组成一个圆，这个圆面是球的一个截面，这个截面垂直于这个点和球心的连线．连接一个切点和球心的直线和这一条切线垂直。

如果切线长为、截面圆的半径为ｒ、球的半径为Ｒ，圆外一点P到球心的距离为d，则

2. 平面与球的位置关系：

平面与球心的距离为d，球的半径为R：

若d＞Ｒ，则平面与球相离（无公共点）。ｄ＝R，平面和球相切（一个公共点），ｄ＜Ｒ平面和球相交（交于一个圆面）。

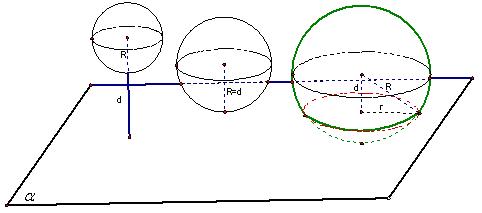
交线是一个圆，圆心与球心的连线垂直于这个平面，如果该圆的半径为r，球的半径为R，球心到平面的距离为d，则

3. 正射影和平行投影：

（1）点的正射影：给定一个平面α，从一点A作这个平面α的垂线，垂足为B，则称B为A在平面α内的正射影。

（2）图形的正射影：一个图形上的各点在平面α上的正射影所组成的图形，称为这个图形在平面α内的正射影。

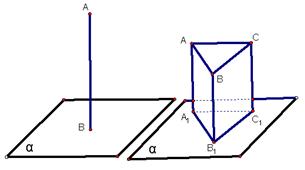
（3）点的平行射影：设直线与平面α相交，称直线的方向为投影方向。过点A作平行于的直线，与平面α的交点B叫做A沿着的方向在平面α上的平行射影。

（4）图形的平行射影：一个图形上的各点在平面α上的平行射影所组成的图形，称为这个图形在平面α内的正射影。

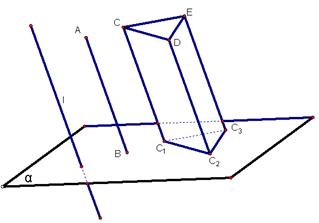
椭圆、双曲线、抛物线都是平面截圆锥面的交线，所以我们称它们为圆锥曲线。

4. 圆锥曲线的性质。

平面上到定点的距离与到定直线的距离的比为常数e的动点的轨迹称为圆锥曲线。这个定点叫圆锥曲线的焦点、定直线叫圆锥曲线的准线。e叫圆锥曲线的离心率。

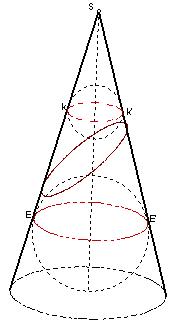
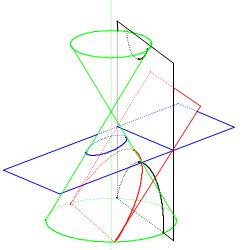
当e＞1时，轨迹为双曲线，0＜e＜1时，轨迹是椭圆；e＝1时，轨迹是抛物线。

【典型例题】

知识点一：球和直线、球与平面的位置关系

例1. 已知球的表面积为2500π，有两个平行截面的面积为49π、400π，求平行截面间的距离。

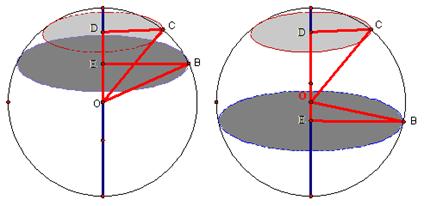
题意分析：球的表面积已知就是已知球的半径，两个平行截面一定是两个圆面，它们的面积已知就是已知它们的半径，可以根据截面的半径计算截面到球心的距离，然后根据两个平行截面到球心的距离计算两个截面的距离，但是由于两个截面可以在球心的同侧也可以在球心的两侧，所以应该分类讨论。

解：如上图，两个平行截面截球所得的两个圆面分别是⊙D和⊙E，设它们的半径分别是r₁、r₂、球的半径为R，它们到球心的距离分别是d₁和d₂，

由于球的表面积为2500π，所以4πR²=2500π， R=25

⊙D面积为49π， 所以πr₁²=49π， r₁=7

⊙E面积为400π，所以πr₂²=400π，r₁=20，

如果两个截面位于球心同侧，则它们的距离d=d₁－d₂=24－15=9

如果两个截面位于球心异侧，则它们的距离d=d₁+d₂=24+15=39

解题后思考：球的截面是一个圆面，它到球心的距离类似于圆的弦心距，这里，两个平面可以在球心的同侧或异侧，有的同学因没有注意到而导致错误。

例2. 有三个球，一个正方体棱长为a，第一个球内切于正方体的六个面，第二个球与这个正方体各条棱都相切，第三个球过这个正方体的各顶点，求这三个球的表面积.

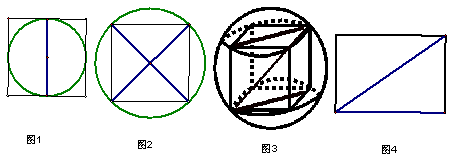
题意分析：正方体的棱长为a，求三个球的表面积，就是利用这些球的性质求它们的半径，第一个球内切于正方体的六个面，其直径恰好等于正方体的棱长，第二个球与这个正方体的各条棱都相切，其直径恰好等于正方体两条相对的棱的距离，也就是正方体侧面的对角线，第三个球过这个正方体的各顶点，其直径等于正方体的对角线，由此可以求出它们的表面积。

解：设三个球的半径依次为R₁、R₂、R₃，则

，

∴它们的表面积

解题后思考：正方体的外接球和内切球的有关性质比较常见，要注意其研究方法。

小结：球和直线、平面的位置关系可以通过类比圆和直线的位置关系来研究

知识点二：正投影和平行投影

例3. 已知△ABC的边BC在平面α内，A在平面α上的正射影为A^/，若∠BAC=90°，求证：△A^/BC为钝角三角形。

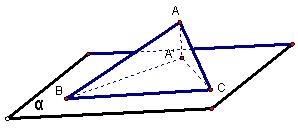
题意分析：已知△ABC为直角三角形，边BC在平面α内，A在平面α内的射影为A^/，要证明△A^/BC为钝角三角形，就是要证明△A^/BC有一个内角为钝角，从图中可以看出就是∠BA^/C为钝角。

解题思路：证明一个角为钝角常用的方法就是证明这个角的余弦或者正切为负值。本题可以由AB²+AC²=BC²，证明A^/B²+A^/C²＜BC²即可

证明：∵AA^/⊥平面α

∴AA^/⊥A^/B，AA^/⊥A^/C

在Rt△AA^/B和Rt△AA^/C中，A^/B＜AB，A^/C＜AC

∴A^/B²+A^/C²＜AB²+AC²=BC²

∴

∴∠BA^/C为钝角，即△A^/BC为钝角三角形

解题后思考：判断三角形形状一般有三种方法：可以证明和某一个三角形相似从而得出其形状，或者像本题一样利用三角形的一个角的余弦或正切的正负，或者利用三角形的边进行判断.

例4. 关于直角∠AOB在平面α的射影有如下判断：①可能是0°的角；②可能是锐角；③可能是直角；④可能是钝角；⑤可能是180°的角，其中正确判断的序号是__________。

题意分析：∠AOB所在平面为β，如果β⊥α，则∠AOB在平面α的射影是一条射线，所以可能是0°也可以是180°的角，如果β∥α，则∠AOB在平面α的射影也是直角，随着平面α和β所成角的变化，∠AOB在平面α的射影可能是锐角或钝角

解：填①②③④⑤

解题后思考：立体几何中利用实物模型可以将抽象的图形转化成具体的实物，同学们可以利用笔、书本、桌子等实物给自己演示。

例5. E、F分别是正方体的面ADD₁A₁和面BCC₁B₁的中心，则四边形BFD₁E在该正方体的面上的射影可能是下图中的 。

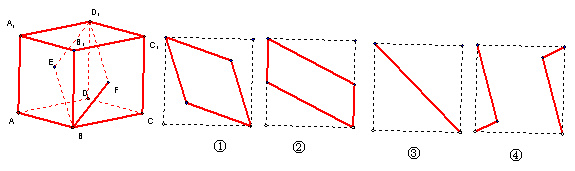
题意分析：这里四边形BFD₁E在该正方体的面上的射影就是正射影，也就是过四边形BFD₁E的四个顶点分别作某个面的垂线，垂足的连线就是四边形BFD₁E在这个面内的射影，正方体有六个面，因为在一对对面内的射影相同，所以我们可以过这四个点分别作三对对面的垂线，将垂足连接就可得到射影。

解：在上、下底面内的射影为②，在面A₁ABB₁和CC₁D₁D内的射影也是②，在AA₁D₁D和BB₁C₁C内的射影为③

故填②③.

解题后思考：基本概念是解决问题的基础，有的同学在解决问题时手足无措的原因就是不知道或不熟悉基本的概念和基本的方法，本题抓住正投影的概念，在各个面中作出正投影即可，这个题目在当年的高考中得分率还是比较低的。

例6. 透明塑料制成的长方体容器ABCD—A₁B₁C₁D₁内灌装一定的水。固定容器底边BC于地面上，再将容器倾斜，随着倾斜程度的不同，有下面五个命题：

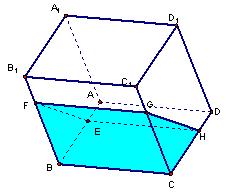
①有水的部分始终呈棱柱形。②没有水的部分始终呈棱柱形。③水面EFGH所在四边形面积是定值.④棱A₁D₁始终与水面所在平面平行。⑤当容器倾斜如丙图时，BE×BF是定值

题意分析：将有水的部分看成以EFBA为底面的几何体可得有水的几何体为棱柱，①正确，同样②也正确。四边形EFGH始终为矩形，且EH长度不变，而EF长度是变化的，所以四边形EFGH的面积是变化的，③错误。由于棱BC是固定在地面不动的，EH和FG始终和棱BC平行，A₁D₁也是始终和EH平行，所以④正确。当E、F在底面上时，由于水的体积是定值，即棱柱EFB－HGC的体积是定值，而高BC也是定值，所以棱柱的底面面积一定，即三角形EFB的面积是定值，也就是BE ×BF是定值，⑤正确。

解：选填①②④⑤

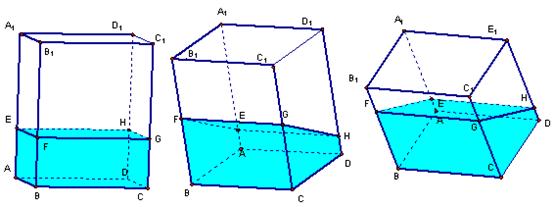
甲 乙 丙

小结：虽然正投影和平行投影是选修中的概念，但是这个概念在立体几何中有广泛的应用，对这个概念的深刻理解有助于对立体几何中相关问题的理解。

本讲涉及的数学思想、方法：

1. 分类讨论的数学思想。平面截圆锥时，根据平面和圆锥的轴的夹角进行分类讨论。

2. 数形结合的数学思想，将综合几何法与解析几何法进行结合来研究圆锥曲线。

预习导学案

（期中复习）

预习前知：

下周我们进行一次期中复习，下周复习测试的重点是选修1—2和选修4—1第一章的内容：框图、推理与证明、数系的扩充、全等与相似、圆与直线、圆与四边形。

【模拟试题】（答题时间：100分钟）

一、选择题：

1. 两条相交直线的平行射影是

A. 两条相交直线 B. 一条直线

C. 一条折线 D. 两条相交直线或者一条直线

2. 如果图形所在平面不平行于投影线，下列说法正确的是：

A. 矩形的平行投影一定是矩形 B. 梯形的平行投影一定是梯形

C. 正方形的平行投影一定是矩形 D. 正方形的平行投影一定是菱形

3. 两条平行直线在同一平面内的平行投影不可能是

A. 两点 B. 直线与直线外一点

C. 一条直线 D. 两条平行直线

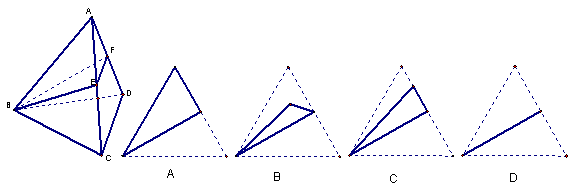
4. 下图中的正四面体，E、F分别是AC，AD的中点，则△BEF在平面ABC内的射影是下列图形中的

5. 球的半径为3，球外一点到球心的距离为6，则过这一点作球的切线和过切点的半径的夹角是

A. 30° B. 60° C. 90° D. 不确定

6. 已知为定直线，F为定点，F，则以F为焦点，为准线的椭圆有

A. 1个 B. 2个 C. 1个或2个 D. 无数个

7. 一平面截球得到直径为6cm的圆。球心到这个平面的距离是4cm，则球的体积是

8. 若圆锥的底面积与轴截面面积之比为π，则圆锥截面的顶角为

A. 60° B. 90° C. 120° D. 150°

二、填空题：

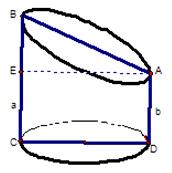
9. 已知底面半径为r的圆柱被一个平面所截，剩下部分母线长的最大值是a，最小值是b，那么截面椭圆的离心率为 。

10. 已知P为△ABC所在平面外一点，O为P在平面ABC上的正射影

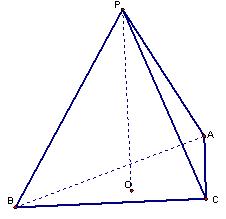
（1）若PA=PB=PC，则O为△ABC的 心。

（2）若PA⊥BC，PB⊥AC，PC⊥AB，则O为△ABC的 心。

（3）若P到直线AB、BC、AC的距离相等，则O为△ABC的 心。

11. 在圆锥内部嵌入丹迪林双球，一个位于平面π上方，一个位于平面π下方，并且都与平面π、圆锥面相切，则与平面π相切的两个切点为所得圆锥曲线的 。

三、解答题：

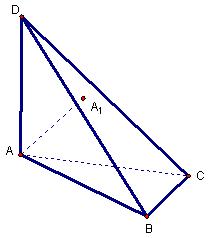
12. 如图，DA⊥平面ABC，△ABC是斜三角形，A₁是A在△DBC上的射影，

求证：A₁不可能是△DBC的垂心。

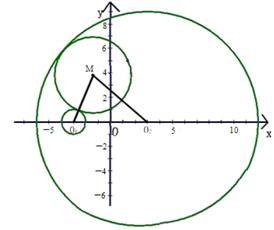
13. 一动圆和已知圆O₁：（x+3）²+y²=1外切，圆O₂：（x－3）²+ y²=81内切，试求动圆圆心的轨迹方程。

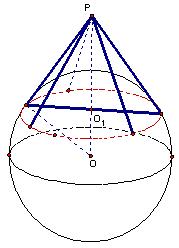
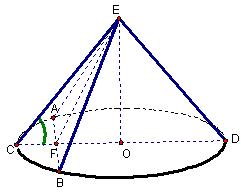
14. 圆锥底面半径为R，母线与底面所成的角为α，锥体内过锥顶E且和高成φ角作一个截面EAB，求截面的面积

【试题答案】

一、选择题：

1. D

解：两条相交直线所在平面和投影方向的线平行时，平行投影是一条直线，不平行时是两条相交直线。选D.

2. B

解：直角的平行投影不一定是直角，故A、C错误，正方形的投影可能是矩形，所以D错误，只有B正确，因为平行线的平行投影仍然平行。

3. B

解：两条平行直线在同一个平面内的平行投影可以是两点、一条直线、两条平行直线

4. B

解：过D作平面ABC的垂线，垂足为△ABC的中心，F为AD中点，过F作平面ABC的垂线，垂足应该在△ABE内部，故应该选B

5. C

解：过切点的球的半径一定垂直于切线。

6. D

7. C

解：由题意得球的半径，所以球的体积

8. B

解：设底面半径为R，则

二、填空题：

9.

解：长轴长为，短轴长为2r，焦距为2（a－b），离心率

10. 解：连接OA、OB、OC，则△POA， △POB， △POC为直角三角形

（1）由于PA=PB=PC，所以OA=OB=OC，所以O为△ABC的外心。

（2）由于PA⊥BC，PB⊥AC，PC⊥AB，∴OA⊥BC，OB⊥AC，OC⊥AB

∴O为△ABC的垂心

（3）若P到直线AB、BC、AC的距离相等，过P作AB，AC，BC的垂线，垂足是E，F，G，连接OE，OF，OG，∴OE=OF=OG则O为△ABC的内心。

11. 焦点

解：结合圆锥曲线的定义可得与平面π相切的两个切点为所得圆锥曲线的焦点。

三、解答题：

12. 证明：假设A₁是△DBC的垂心，则BA₁⊥CD，由于A₁A⊥平面BCD于A₁，

∴AB⊥CD，又DA⊥平面ABC∴AB⊥AC，所以这与△ABC是斜三角形矛盾，故A₁不可能是△DBC的垂心

13. 解：设动圆圆心为M（x，y）、半径为R，则|MO₁|=1+R， |MO₂|=9－R

∴|MO₁|+|MO₂|=10>|O₁O₂|，由椭圆的定义，M为以O₁、O₂为焦点，2a=10的椭圆，∴动圆圆心的轨迹方程为

14. 解：作垂直于AB的底面直径CD，交AB于F，则∠ECD=α，

∠FEO=φ，∵OC=R∴EO=Rtanα，FO=EOtanφ=Rtanαtanφ