【本讲教育信息】

一、教学内容：

初三总复习7：浮力的复习

二、学习目标

1. 应用计算浮力的三种方法。

2. 经历从提出猜想和假设到进行实验探究的过程，发现浮力的大小和液体的密度及排开液体的体积的关系，从而认识阿基米德原理。

3. 通过对物体的浮沉现象的研究，知道物体的浮沉条件。

4. 通过物体浮沉条件的应用，了解物理知识在生产、生活和社会中的应用；知道密度计、潜水艇、气球的原理。

三、重点难点

重点内容：阿基米德原理的实验探究过程，理解阿基米德原理。

能应用计算浮力的三种方法进行计算，从而来解决实际生活中的问题。

熟知物体的浮沉条件及其应用。

难点内容：对阿基米德原理的理解；

浮力的三种计算方法的灵活应用；

物体的浮沉条件及其应用。

【跨越障碍与典型例题】

一. 什么是浮力

船可以浮在水面，潜水艇能潜入水下航行，节日放飞的气球可以升到空中，金鱼可以轻盈地在水中上下游动等等是一些有关浮力的问题。

（1）放入水中的木块放手后，木块从水里浮上来，最后浮在水面上静止不动。可见，从水里浮上来的物体和浮在水面上的物体都受到浮力。

（2）把石块放入水中，我们发现放手后石块在水中下沉，并且一直沉到水底。下沉的石块受浮力作用吗？

为研究这个问题，我们通过实验来进行：

①先用细线将石块系住，挂在弹簧秤下，测出其在空气中的重力G_空

②用弹簧秤拉着石块全部浸没有水中，观察此时弹簧秤的示数F_示（也可叫做石块在水中时的视重）。我们发现这时弹簧秤的示数比在空气中小了。这个实验就充分证明浸入水中的石块（在液体中下沉的物体）也受到浮力。

③我们还可以感受一下这个浮力的大小和方向，竖直向上就是浮力的方向。

（3）浸在液体中的物体要受到液体对它的竖直向上的浮力，在气体中的物体也要受到气体对物体的浮力。

综上所述：

（1）一切浸在液体或气体中的物体受到的液体或气体对它竖直向上托的力叫做浮力。

（2）浸在液体中的物体所受到的浮力可用公式：F_浮＝G_空－F_示来计算。

例1. 有一个合金块质量10kg，全部浸没在水中时，需用80N的力才能拉住它，求：此时合金块受到的浮力多大？

分析：根据G＝mg可得出合金块重力，浮力大小是重力与拉力的差。

解答：G＝mg＝10×9.8N／kg＝98N

F_浮＝G－F_浮＝98N－80N＝18N

答：合金块受到的浮力是18N。

二. 阿基米德原理

1. 与浮力大小相关的因素

（1）轮船从江河中航行到大海中，吃水的深度变化了。再如把鸡蛋放入清水中，发现鸡蛋沉入水中，当向水中加盐时，发现鸡蛋上浮到液面。这使我们猜想到：物体所受浮力的大小可能与液体的密度有关系。

（2）从井中提水，盛满水的桶露出水面越多，提桶要用的力就越大。再如我们把一个物体用细线系住，挂在弹簧秤的下面，逐渐浸入水中，我们发现弹簧秤的示数越来越小，这说明物体所受的浮力大小还可能与物体排开液体的体积有关系。

（3）有的同学可能还猜想到，物体所受浮力的大小可能与物体在液体中的深度有关。我们试一试。将一个物体挂在弹簧秤下，浸没在水中，并改变物体在水中的深度，观察弹簧秤的示数，我们发现弹簧秤的示数没有变化，这也就说明了物体所受浮力的大小与物体在液体中的深度没有关系。

（4）有的同学可能还猜想到物体所受到的浮力还可能与物体的形状有关系。我们将一块橡皮泥挂在弹簧秤下，浸没在水中，记下弹簧秤的示数，然后拉出橡皮泥，并改变其形状后再次浸入水中，观察弹簧秤的示数有无变化。我们发现弹簧秤的示数没有变化，这说明物体在液体中所受浮力的大小与物体的形状也没有关系。

综上所述：物体在液体中所受浮力的大小不仅与液体的密度有关，还与物体排开液体的体积有关，而与浸没在液体中的深度和物体的形状等因素无关。

2. 探究浮力的大小

溢水杯中盛水，使水面跟溢水杯管口相平，弹簧秤甲吊着铁块，弹簧秤乙吊着一个小容器，并使溢水杯中溢出的水能流入小容器中。

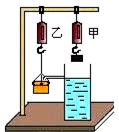
将铁块部分浸入水中，弹簧秤甲减小的示数与弹簧秤乙增大的示数相等。再将铁块全部浸入水中，发现甲弹簧秤示数减小的仍等于乙弹簧秤示数增加的。甲弹簧秤示数减小的原因是因为铁块在水中受到浮力，浮力大小就是弹簧秤甲的示数减小数值，弹簧秤乙示数增加的原因就是因为溢水杯中流出的水使其重力增大。溢水杯溢出的水就是铁块在水中所排开的水。所以：铁块在水中受到的浮力大小总是跟它排开水的重力相等。

这个结论就是著名的阿基米德原理：浸在液体里的物体受到向上的浮力；浮力的大小等于物体排开的液体受到的重力。

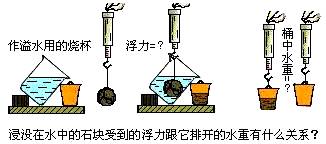
如果你对上面的实验感到较难理解的话，课本上这个实验则较容易。我们通过这个实验所得到的结论是相同的，也就是物体在液体中所受到的浮力等于它排开的液体受到的重力，它排开的液体越重，它受到的浮力越大。

对阿基米德原理的几点说明：

a. 物体在液体中，不论是部分浸入还是全部浸入，均受到浮力作用；

b. 浮力的大小和排开的液体所受的重力的大小相等；

c. 本原理不仅适用于液体，也适用于气体；

d. 原理的数学表达式为

F_浮＝G_排液

或F_浮＝ρ_液V_排液g

或F_浮＝ρ_液V_物浸g

这里要说明的是什么是V_排液。V_排液就是V_物浸。也就是物体排开液体的体积。当物体在液面以下时，V_排液＝V_物体。当物体漂浮在液面上时，V_排液＜V_物体

例2. 质量是2.7kg的铝块，一半浸入水中时，所受浮力多大？完全浸没在酒精中时，所受浮力多大？（ρ_铝＝2.7×10³kg／m³，ρ_酒精＝0.8×10³kg／m³）

分析：在水中时排开水的体积等于物体体积的一半；在酒精中时排开酒精的体积等于物体体积。

解答：

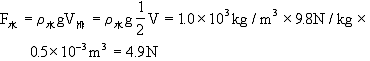
答：在水中受到的浮力是4.9N，在酒精中受到的浮力是7.84N。　

例3. 一个实心石块，在空气中用弹簧秤测时示数是10N，当把石块完全浸没在水中时，弹簧秤测得示数是6N，求：石块密度。

分析：弹簧秤在空气中测得的示数等于物体的重力，由此可得出石块质量。利用弹簧秤测石块时在空气中和水中的两次示数差，可得出石块所受的浮力，即可求出石块的体积。　

解答：

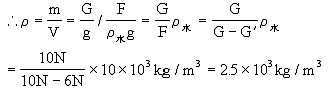
答：石块的密度是。

三. 物体的浮沉

既然一切浸入液体中的物体都受到液体对它竖直向上的浮力，为什么物体有的上浮、有的下沉、有的还可停留在液体中的任何地方呢？

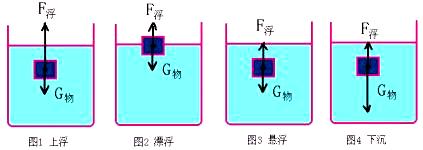
如图1所示，一个木块放入水中后，其要在水中向上运动，我们称其为上浮。显然它受到不平衡力的作用，此时木块所受到的浮力大于重力，二者的合力向上。

当木块上浮到液面时，它不会从液面处飞向天空，而是停在液面上，我们称这种状态为漂浮。显然它受到平衡力的作用。所以物体处于漂浮时，它受到的浮力必然要等于重力。

当某一木块可以停在液体中的任何一个深度的地方，我们称这种状态为悬浮。悬浮的物体也是处于静止状态，当然，其受到的浮力与重力相等。如图3所示。

由物体处于漂浮和悬浮的条件可知，其都是所受到的浮力与重力相等，这样就为我们求漂浮和悬浮的物体所受到的浮力提供了一种方法，也就是平衡法。这时F_浮＝G_物。但这只适用于物体处于平衡状态的情况。

如图4所示。如果物体向下运动，我们把这种情况称之为下沉。由上面的分析不难看出物体下沉时，它所受到的浮力小于重力。浮力与重力的合力是向下的。

综上：

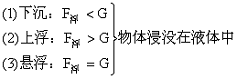
（4）漂浮：F_浮＝G——物体的一部分浸入液体中

说明：

（1）物体上浮、下沉是运动过程，此时物体受非平衡力作用。下沉的结果是沉到液体底部，上浮的结果是浮出液面，最后漂浮在液面。

（2）漂浮与悬浮的共同点都是浮力等于重力，在平衡力的作用下静止不动。但漂浮是物体在液面的平衡状态，物体的一部分浸入液体中。悬浮是物体浸没在液体内部的平衡状态，整个物体浸没在液体中。

四、浮力与密度

上面是物体的浮沉条件的一种表述——合力表述；物体的浮沉条件还有另一种表述——密度表述。结合合力所述与阿基米德原理，我们可以证明如下：

（1）当物体漂浮时，F_浮＝G_物

又因为F_浮＝ρ_液gV_排 G_物＝ρ_物V_物g

所以ρ_液gV_排 ＝ρ_物V_物g

也就是ρ_液V_排 ＝ρ_物V_物

由于物体处于漂浮状态，其必然有一部分体积露出水面，也就是说V_排 ＜V_物，所以ρ_液 ＞ρ_物。

（2）当物体上浮时，F_浮＞G_物

又因为F_浮＝ρ_液gV_排 G_物＝ρ_物V_物g

所以ρ_液gV_排 ＞ρ_物V_物g

也就是ρ_液V_排 ＞ρ_物V_物

由于物体处于上浮状态，还没有露出液面外，其必然全部浸没在液体中，

也就是说V_排 ＝V_物，所以ρ_液 ＞ρ_物。

（3）当物体悬浮时，F_浮＝G_物

又因为F_浮＝ρ_液gV_排 G_物＝ρ_物V_物g

所以ρ_液gV_排 ＝ρ_物V_物g

也就是ρ_液V_排 ＝ρ_物V_物

由于物体处于悬浮状态，其必然全部浸没在液体中，

也就是说V_排 ＝V_物，所以ρ_液 ＝ρ_物。

（4）当物体下沉时，F_浮＜G_物

又因为F_浮＝ρ_液gV_排 G_物＝ρ_物V_物g

所以ρ_液gV_排 ＜ρ_物V_物g

也就是ρ_液V_排 ＜ρ_物V_物

由于物体处于下沉状态，其必然全部浸没在液体中，

也就是说V_排 ＝V_物，所以ρ_液 ＜ρ_物。

提醒：物体的浮沉条件的两种表述形式，各有所用，同学们只有加深对其的理解才能正确应用。

例4. 质量相同的实心木块、铝块、铜块同时放入足够深的水槽中静止时，三个物体所受的浮力 ［ ］

A. 木块最大 B. 铝块最大　　 C. 铜块最大 D. 一样大

分析：因木块密度小于水的密度，铝块和铜块的密度大于水的密度。因此木块将漂浮在水面上而铝块和铜块将浸没在水中，木块所受浮力大小等于重力，铝块和铜块所受浮力比重力小。

解答：A。

说明：由于铝密度小于铜，质量相等时，铝块体积大于铜块体积，根据浮力公式F_浮＝ρ_水gV_排可知，铝块浮力大于铜块浮力。　

例5. 一个木块漂浮在水面上静止时，有体积露出水面外，求木块的密度是多大？

分析：木块漂浮在水面时，浮力等于重力大小，据此可求出木块的密度与水的密度的关系。

解答：设木块体积为V_木

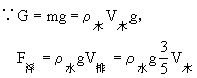
答：木块的密度是

说明：解题时必须搞清V_排与V_物的关系。

五. 浮力的利用。

这两幅图片，同学们一定不陌生，这是人们对浮力的有效利用。除此，浮力还有很多的应用。

1. 密度计

密度计是测量液体密度的仪器。

密度计的工作原理是这样的：由于它受到的重力是一定的，漂浮时，浮力等于重力，无论把它放到哪种液体中，受到的浮力总是相同的。因而把它放到密度较大的液体中，它能够排开的液体较少，浸入的深度就小些；反之，把它放到密度较小的液体中，浸入的深度就大一些；于是，根据它浸入的深度就可以测量液体的密度。

密度计刻度值上小下大：密度计是根据物体漂浮时的受力平衡及阿基米德原理而制成的。从物体沉浮条件可知，浮在液面上的物体符合：F_浮＝G。由于密度计的重力G不变，所以它受到的浮力F_浮是一定的.又F_浮＝ρ_液gV_排可知.ρ_液大时V_排就小，V_排小表示密度计在液体中浮得浅些，所以表示密度大小的刻度值就大，使密度计上的刻度值呈现上小下大。

思考：轮船的吃水深度与密度计的原理有什么相同之处？

2. 盐水选种

盐水选种是我国古代劳动人民发明的一种巧妙的挑选种子的方法。

盐水选种，就是把种子放在一定浓度的盐水里，利用浮力把好种子和坏种子区分开来。选小麦种子的盐水是把盐水配成密度在（1.16~1.2）×10³千克/米³之间。把小麦放在这样浓度的盐水里，密度超过1.2×10³千克/米³的好种子都沉在水底，因为它们受到的浮力小于它们的重力，密度小于（1.16~1.2）×10³千克/米³的坏种子都在盐水中浮起来，这样好种子与坏种子就很容易地被分开了。

3. 潜水艇

潜水艇在水中可以自由浮沉，因此它是军事上的一种重要舰艇。

通过春节晚会上的小品“水下除夕夜”，可以简单了解潜水艇的构造及工作环境。

潜水艇可以潜入水下航行，进行作战或侦察，是根据阿基米德原理制造的。当它潜水和上浮时是靠改变它自身的重量来实现的。潜水艇的侧面有水舱，当它下潜时，使水舱充水，于是艇身重量增大，潜艇就逐渐下沉。当水舱中充入适量的水时，潜艇就能在水中任何位置上停留，此时潜艇的重量等于浮力。当潜艇需要上浮时，可用压缩空气将水排出，当艇身的重量减小到小于浮力时即浮出水面。

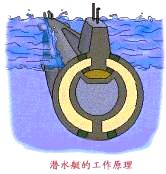
阿基米德原理告诉我们：浸在液体中的物体受到一个向上的浮力，它的大小等于物体所排开的液体受到的重力。所以，水舱储藏水量的多少是潜水艇上浮、下沉、保持深度的一个重要因素。

4. 气球和飞艇

同液体有浮力一样，空气也有浮力。气球和飞艇就是利用空气的浮力升入空中的。

气球和飞艇的主要组成部分是气囊。气囊内充有密度比空气小的气体，如热气、氢气或氦气。如果气球或飞艇的自重加上所载物体的重量小于气囊排开的空气重量，即小于受到的升力，气球或飞艇就会升入空中。由于高空中空气越来越稀薄，密度在减小，所以气球或飞艇所受的升力等于它受到的重力，就不再上升而停在某一高度漂浮。当需要降落时，只需放出气囊中的部分气体就行。

另外，在医学上，浮力还有一个特殊的用途——水疗法。如果病人的四肢肌肉或关节有病、受伤，医生可以让他浸在水中，利用身体受到的浮力作用，使病人只要用很小的力，就能使四肢活动，从而进行治疗。

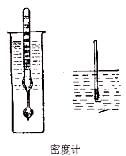
例6. 现将一支密度计先后放在密度分别为ρ₁和ρ₂的液体中，如图，试比较两种液体的密度。

分析：密度计是测定液体密度的仪器。它是漂浮在液面的，所以在不同液体中所受的浮力相同，都等于密度计的自身重力。它排开液体的体积不同，说明液体的密度不同，当它浸入密度大的液体中时，它排开液体的体积就小，露出液面的部分较多。

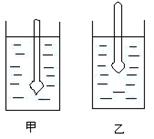
解：F₁＝F₂＝G

ρ₁gV₁＝ρ₂gV₂

∵V₁>V₂

∴ρ₁<ρ₂

说明：密度计是利用物体浮在液面上的条件来工作的，它是测定液体密度的仪器。它是个密封的玻璃管，下端装有小弹丸（如铅丸）或水银，使它能竖直地浮在液体中。管上有刻度，它的刻度值一般标的是液体的密度与水的密度的比值，如果密度计的读数是1.6，则表示这种液体的密度是水的密度的1.6倍，它的密度则是1.6×10³千克／米³。

例7. 一块石蜡，放在酒精中将下沉，放在水中将上浮，请判断出这块石蜡的密度在什么范围内？如何利用一只量筒及适量的酒精和水，精确地测出石蜡的密度？（ρ_酒精＝0.8×10³千克／米³）

解答：由石蜡放在酒精中将下沉可知 ρ_蜡>ρ_酒精

由石蜡放在水中将上浮可知 ρ_蜡<ρ_水 则ρ_酒精<ρ_蜡<ρ_水

即石蜡的密度在0.8×10³千克／米³和1.0×10³千克／米³之间。

精确地测定石蜡的密度，步骤如下：

（1）向量筒中倒入适量的水，记下水的体积V₁；

（2）将石蜡块放入量筒中，记下水的体积V₂；

（3）取出量筒中的水和石蜡块，再往量筒中放入适量的酒精，记下酒精的体积V₃；

（4）将石蜡块放入量筒，浸没于酒精中，记下此时液体的体积V₄；

（5）根据上述数据计算石蜡块的密度

F_浮＝ρ_水gV_排1＝ρ_水g（V₂－V₁）；

根据浮沉条件

F_浮＝G_蜡＝m_蜡g＝ρ_蜡gV_蜡＝ρ_蜡g（V₄－V₃）

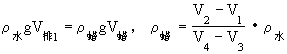
【模拟试题】（答题时间：80分钟）

一. 选择题

1. 把两个质量相同的铁球和铝球，分别挂在弹簧秤上，然后将它们全部浸入水中，则弹簧秤的示数（ ）

A. 挂铁球的大； B. 挂铝球的大；

C. 两种弹簧秤的示数相等； D. 不能确定

2. 关于阿基米德原理，正确的叙述是（ ）

A. 浸入液体中的物体受到向上的浮力，浮力的大小等于它排开的液体的体积；

B. 浸入水中的物体受到向上的浮力，浮力的大小等于它排开的水受到的重力；

C. 浸没在液体中的物体受到向上的浮力，浮力的大小等于它排开的液体受到的重力；

D. 浸入液体中的物体受到向上的浮力，浮力的大小等于物体受到的重力；

E. 浸入液体中的物体受到向上的浮力，浮力的大小等于它排开的液体受到的重力．

*3. 将同一物体放在液体中的三种情况如图所示，比较它受到的浮力大小，表示浮力最小的是（ ）

A. 图甲； B. 图乙； C. 图丙； D. 无法比较

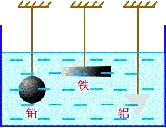
4. 如图所示，体积相同、形状不同的铅球、铁板和铝块，浸没在水中不同深度的地方，则（ ）

A. 铝块受到的浮力大，因为它浸入液体中的深度大；

B. 铅球受到的浮力大，因为它的密度大；

C. 铁板受到的浮力大，因为它的面积大；

D. 铅球、铁板、铝块受到的浮力一样大。

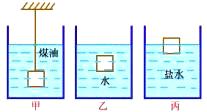
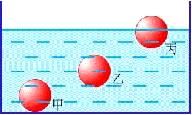
*5. 甲、乙、丙三个体积不同的小球放在液体中，静止时小球所在的位置如图所示。比较三个小球的密度（ ）

A. 甲最大； B. 乙最大； C. 丙最大； D. 一样大

6. 潜水艇由海面上10米深处下潜到20米的深处的过程中，海水对它的（ ）

A. 压强增大，浮力增大； B. 压强增大，浮力不变；

C. 压强、浮力都不变； D. 压强差、浮力都不变

7. 等质量的木块和冰块，漂浮在水面，它们受到的浮力之比______，它们排开的液体体积之比______，它们露出水面的体积之比______（ρ_水＝0.6克/厘米³，ρ_冰＝0.9克/厘米³）． ［ ］

A. 1∶1 　 B. 2∶3　　 C. 3∶1 　　 D. 6∶1　

二. 填空题

1. 浮力的施力物体是_____，浮力的方向是______的．浮力的大小跟______和______有关。

2. 阿基米德原理的表达式是F_浮＝G_排液＝______．式中的V_排只有______时才等于V_物。

3. 浸没在液体中的物体，如果其密度______于液体的密度，物体就上浮；如果其密度______于液体的密度，物体就悬浮；如果其密度______于液体的密度，物体就下沉。（填：“大”、“小”或“等”）

4. 浸没在水中的木块，它受到的水的浮力______于它的重力，所以木块上浮；当它露出水面并继续上浮时，它的排水体积______，它受到的浮力______；当它静止在水面上的时候，木块受到的浮力______于它受到的重力。（填：“变大”、“不变”、“变小”）

5. 漂浮在液面的物体受到两个力的作用，它们是向上的______力和向下的______力．由于物体静止在液面上，这两个力的关系是______，可见，物体浮在液面上的条件是______．

6. 浸没在水中的石块受到的浮力是1牛，它排开的水的重是______牛．如果石块的一半体积浸入水中，则此石块受到的水的浮力是______牛．

7. 质量相等的铁球和铝球放入水中，铁球受到的浮力______于铝球受到的浮力。放入水银中，铁球受到的浮力______于铝球受到的浮力。（填：“大”、“等”、“小”）

*8. 一个物体漂浮在酒精中，它浸入酒精中的体积是100厘米³，这个物体重______牛，将它放入水中，它受到的浮力是______牛，它浸入水中的体积是______厘米³．（g＝10牛/千克）

9. 重5牛、体积是0.6分米³的物体浸没在水中，松手后它将______．（填：“上浮”、“下沉”、“悬浮”）（g＝10牛/千克）

*10. 一块冰浮在水面上，它浸入水中的体积是冰的体积的______倍．（ρ_冰＝0.9×10³千克/米³）

11. 一艘轮船自重是5×10⁷牛，最大载货量是10⁸牛，则这艘轮船的排水量是______吨．如果船到港口将货物卸下5×10⁷牛，则轮船所受到的浮力是______牛，它的排水体积减少______米³。（设：轮船在内河航行）（g取10牛/千克）

12. 潜水艇是靠改变______来实现浮沉的。气球、飞艇的主要组成部分是______，在这里面装着______比空气小的气体，当气球或飞艇受到的浮力______于气球、飞艇的自重加载重时，气球、飞艇就能上升。

三. 实验题

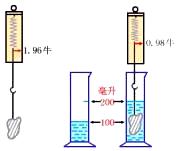
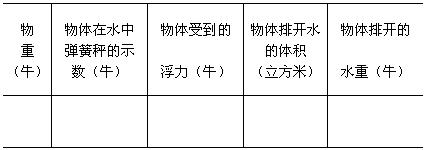
把从下图所示实验中观察到的弹簧秤和量筒的示数记录在表格中，并计算出相应的物理量。

从这个实验中得出的结论是：____________。

四. 计算题

1. 一个体积为2米³的氢气球，球皮重10牛，在地面附近空气对它的浮力是多大？它最多能吊起多重的物体？（ρ_空气＝1.29千克/米³，ρ_氢气＝0.09千克/米³，g＝10牛/千克）

*2. 有一个金属球，在空气中称量时，弹簧秤的示数是15牛，浸没在水中称量时，弹簧秤的示数是5牛，已知该金属的密度为2×10³千克/米³，g＝10牛/千克．求：

（1）这个金属球的体积多大？

（2）这个金属球是空心的还是实心的？

（3）如果是空心的，空心部分的体积多大？

**3. 密度是0.6×10³千克/米³的木块，体积是2米³，当它浮在水面上时，求：（g＝10牛/千克）

（1）木块的重力；

（2）木块受到的浮力；

（3）木块排开的水的体积；

（4）木块露出水面的体积．　

【试题答案】

一.

1. A 2. E 3. A 4. D 5. A 6. B，D 7. A，A，D

二.

1. 液体，竖直向上，液体密度，排开液体的体积

2. ρ_液gV_排，当物体浸没在液体中

3. 小，等，大

4. 大，变小，变小，等

5. 浮，重，二力平衡，F_浮＝G_物

6. 1，0.5

7. 小，等

8. 0.8，0.8，80

9. 上浮

10. 0.9

11. 15000，10⁸，5×10³

12. 自重，气囊，密度，大

三.

1.96，0.98，0.98，1×10^－4，0.98．这个物体在水中受到的浮力等于它排开的水受到的重力．

四.

1. 25.8牛，15.8牛．

2. 1分米³，空心的，0.25分米³．

3. 1.2×10⁴牛，1.2×10⁴牛，1.2米³，0.8米³