【本讲教育信息】
一. 教学内容：
中心对称与四边形单元小结
二. 学习重难点：
中心对称与中心对称图形是本节课的重点也是难点，而四边形的知识结构是重点，综合应用是难点
三. 知识要点讲解：
【两个图形关于某个点成中心对称】
1. 特殊的旋转----------中心对称（旋转180°）
问题：（1）如果将半圆M绕点O旋转180°后，它能与半圆N重合吗？
（2）如果将△ABC绕点P旋转180°后，它能与△A′B′C′重合吗？
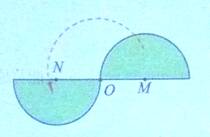
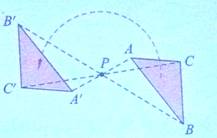
定义：在平面内，如果把一个图形绕某个点旋转180°后，能与另一个图形重合，那么就说这两个图形关于这个点成中心对称，这个点叫做对称中心，旋转180°后重合的两个点叫做对应点。
注意：中心对称是两个图形之间的位置关系。
2. 作出某图形关于某点成中心对称的图形：
1）、作点A关于点O成中心对称的点A′，
作法：
2）、作△ABC关于点O成中心对称的△A1B
分析：要作出△ABC关于点O成中心对称的△A1B
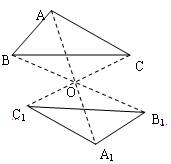
探讨成中心对称的两个图形的性质：
性质：①、成中心对称的两个图形全等
②、成中心对称的两个图形上的每一对对应点所连成的线段都被对称中心平分。
3. 平面直角坐标系中关于原点O成中心对称的点的坐标的特点
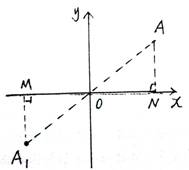
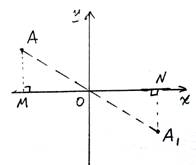
坐标特点：横纵坐标都是互为相反数，即：
点A（a，b）关于原点O的对称点的坐标是（－a，－b）
【中心对称图形】
1. 中心对称图形
思考：将“风车”绕点O旋转180°，旋转前后的图形重合吗？
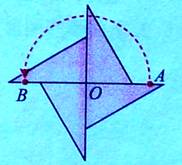
定义：在平面内，一个图形绕某个点旋转180°，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心。
性质：中心对称图形上的每一对对应点所连成的线段都被对称中心平分
2、做一做：
（1）猜想：平行四边形是中心对称图形吗？如果是，对称中心是什么？
（2）结论：平行四边形是中心对称图形，它的对称中心是对角线的交点。
（3）正方形是中心对称图形吗？正方形绕两条对角线的交点旋转多少度能与原来的图形重合？能由此验证正方形的一些特殊性质吗？
3、想一想：
（1）正三角形是中心对称图形吗？
（2）正五边形是中心对称图形吗？
（3）正六边形是中心对称图形吗？
（4）除了平行四边形，你还能找到哪些多边形是中心对称图形？
归纳：中心对称的图形很多，如边数为偶数的正多边形都是中心对称图形。
练一练：1） 世界上因为有了圆的图案，万物才显得富有生机，以下来自现实生活的图形中都有圆，它们看上去是那么美丽与和谐，这正是因为圆具有轴对称和中心对称性。请问以下三个图形中是轴对称图形的有 ，是中心对称图形的有 。
A. 一石激起千层浪
B. 方向盘
C. 铜钱
2）下图中，哪个“风车”是中心对称图形？
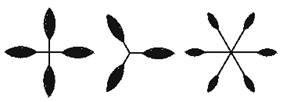
A B C
3）下列四张扑克牌的牌面，不是中心对称图形的是（
）
A B C D
4）下列图形中，既是轴对称图形又是中心对称图形的是（ ）
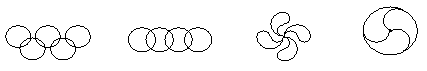
A B C D
【单元总结】
第九章 四边形性质的探索
（一）四边形和各种特殊四边形的关系图
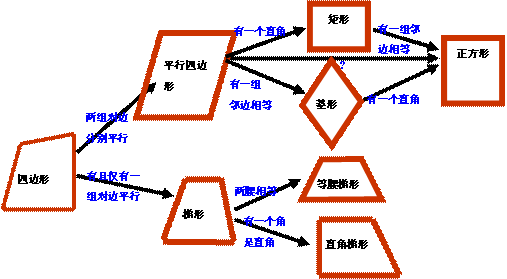
（二）特殊四边形的性质
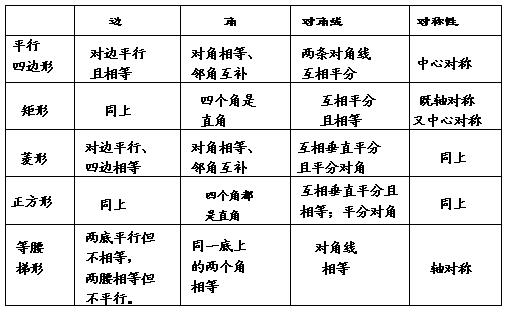
（三）中心对称图形与两个图形关于某个点成中心对称
（四）多边形的内角和与外角和
（1）ｎ边形的内角和等于（ｎ－2）·180°（每个内角的度数是
）
（2）多边形的外角和都等于360°（正多边形的每一个外角等于
）
方法总结：利用上面这两个公式列方程解方程可以求多边形的边数的问题。
（五）平面图形的密铺
密铺的条件：用多边形进行密铺时，相拼接的边相等，每个拼接点处各个角的和等于360°
密铺中规律性的结论：
①用同一种三角形和同一种四边形都可以进行密铺（其它具有特殊条件的多边形也可以密铺）；
②如果只用一种正多边形进行密铺，那么只有正三角形、正方形和正六边形可以密铺。
③如果用两种图形密铺，正三角形和正四边形可以密铺，正四边形和正六边形可以密铺，也可以同时用三种图形密铺。
六、本章学习的主要数学思想方法有：转化思想（把多边形的问题转化为三角形或四边形）；化归思想（把菱形、梯形的计算问题化归为直角三角形的问题解决）；另外还有方程思想的运用（列方程解方程求多边形的边数）
如图：
【中考链接】
例1、下列命题中错误的是（ ）
A、平行四边形的对边相等 B、两组对边分别相等的四边形是平行四边形
C、矩形的对角线相等 D、对角线相等的四边形是矩形
总结：此题考查了特殊的平行四边形的判定
例2、如图：矩形纸片ABCD，AB=2，点E在BC上，且AE=EC．若将纸片沿AE折叠，点B恰好落在AC上，则AC的长是 ．
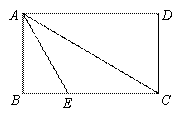
总结：此题考查了轴对称即三线合一的性质和勾股定理
例3、如图，P为菱形ABCD的对角线上一点，PE⊥AB于点E，PF⊥AD于点F，PF=
答案：PE=
总结：此题考查了菱形的性质及点到直线的距离以及角平分线的性质
例4、若一个多边形的内角和等于
，则这个多边形的边数是（ ）
A、5 B、
总结：此题考查了多边形的内角和定理
例5、如图，在梯形ABCD中，AD∥BC，E为BC上一点，DE∥AB，AD的长为1，BC的长为2，则CE的长为 ________．
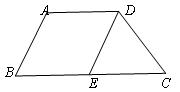
答案：CE=1
总结：此题考查了平行四边形的判定与性质，学习了梯形的研究方法。
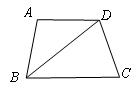
例6、如图，梯形
中，
，
，
，
，则
（ ）
A、
B、
C、
D、
总结：此题考查了等腰三角形的性质与平行线的性质
【课堂小结】
本节课我们主要研究了中心对称与中心对称图形及其性质，总结了本章的知识结构，以及梯形中的辅助线的添加。
【模拟试题】（答题时间：90分钟）
一、细心选一选，你一定能行（每题2分，共20分）
1、下面给出的图形能密铺的是（ ）
A、正五边形 B、三角形 C、正十边形 D、正十二边形
*2、某学生在计算四个多边形的内角和时，得到了如下四个答案，其中错误的是（ ）
A、800° B、180° C、720° D、1800°
3、在如图所示的图案中，即不是轴对称图形，又不是中心对称图形的是（ ）
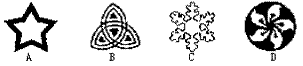
4、能判定一个四边形是正方形的条件是（ ）
A、对角线相等，对边平行且相等 B、一组对边平行，一组对角相等
C、对角线互相垂直平分且相等 D、一组邻边相等，对角线互相平分
*5、在四边形ABCD中，∠A、∠B、∠C、∠D的度数比为1∶2∶2∶3，这个四边形是（ ）
A、平行四边形 B、等腰梯形 C、梯形，但不是等腰梯形 D、直角梯形
6、如图，在平行四边形ABCD中，∠B＝60°，AB＝5cm，则下面正确的是（ ）
A、BC＝5cm，∠D＝60° B、∠C＝120°，CD＝5cm
C、AD＝5cm，∠A＝60° D、∠A＝120°，AD＝5cm
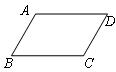
7、如图，AC，BD是平行四边形ABCD的对角线，AC与BD交于点O，AC＝4，BD＝5，BC＝3，则△BOC的周长是（ ）
A、7.5 B、12 C、6 D、无法确定．
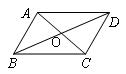
8、如图，AC，BD是菱形ABCD的对角线，且相交于点O，则下面说法正确的是（ ）
A、图中共有8个三角形, 它们不全等．
B、图中只有四个全等的直角三角形
C、图中有四对不是直角的全等三角形
D、图中有四个全等的直角三角形, 两对全等的等腰三角形
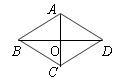
*9、等腰梯形ABCD的对角线相交于点O，则可以找到的全等三角形有( )
A、1对 B、2对 C、3对 D、4对
*10、一矩形两对角线之间的夹角有一个是60°，且这角所对的边长为5cm，则对角线长为（ ）
A、5 cm B、10cm C、5
cm
D、无法确定
二、仔细填一填，你一定很准（每题2分，共20分）
11、十边形的内角和是 度．
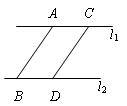
12、如图，AB和CD是夹在两平行线l1、l2之间的平行线段，则AB CD（填“＞”或“＜”或“＝”）．
13、一个矩形的对角线长10cm，一边长6cm，则其周长是 ，面积是 ．
14、在梯形ABCD中，AD∥BC，AB＝CD，直线DE∥AB，DE把梯形分成两个图形，一个是 ，另一个是 ．
*15、若一个四边形的内角的度数之比为2∶2∶1∶4，则这个四边形最小内角的度数为_____．
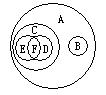
16、如图所示中①四边形，②平行四边形，③矩形，④正方形，⑤菱形，⑥梯形，用集合示意图中的字母代表分别填入下列横线上：①＿＿＿；②＿＿＿；③＿＿＿；④＿＿＿；⑤＿＿＿；⑥＿＿＿．
17、菱形的一个内角为60°，且平分这个内角的邻角的平分线长为8cm，则这个菱形的周长是________．
18、矩形的面积为12cm2，一边长为4cm，那么矩形的对角线长是________．
*19、若一个n边形的内角和是它的外角和的11倍，则n＝_______．
*20、平行四边形ABCD的周长为60cm，AC和BD相交于点O，△AOB的周长比△OBC的周长大8cm，则平行四边形ABCD的边长分别为_______．
三、认真做一做，你一定成功（共40分）
21、将一个三角形经过怎样的旋转能得到一个平行四边形？并说说你的理由．
22、一菱形周长为20cm, 其一对角线长6cm，求菱形的面积．
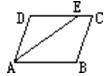
23、如图，在平行四边形ABCD中，∠DAB的平分线交DC于点E．若∠DEA＝32°，试求平行四边形ABCD各内角的度数．
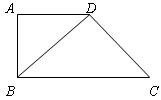
*24、如图，在梯形ABCD中，AD∥BC，∠B＝90°，AD＝AB＝2，且BD＝CD，求
△DBC的周长和梯形ABCD的面积．
25、小明家准备在客厅铺设地板砖．客厅地面是一个矩形，长6.3米，宽4.8米．装修工人提出两个建议，一是铺设80cm×80cm的地板砖，每块40元；二是铺设60cm×60cm的地板砖，每块25元．小明要求材料费少，又铺得整齐为好，你能帮他出个好主意吗?
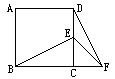
*26、如图，正方形ABCD中，E为CD边上一点，F为BC延长线上一点，CE＝CF，若∠BEC＝60°．求∠EFD的度数．
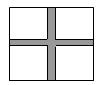
*27、如图是一个正方形的花坛，边长为10米．在花坛上建两条相互垂直的小道，把花坛分为四个面积相等的部分，小道宽1米．问面积相等的部分各为多少?
28、在所学过的线段、角、等腰三角形、平行四边形、菱形、矩形、正方形、等腰梯形、正五边形、正六边形等图形中，你认为哪些图形是轴对称图形，哪些图形是中心对称图形，哪些图形既是轴对称又是中心对称图形？说说你的理由，并指出它们的对称轴或对称中心．
四、综合创新，你一定很棒（共20分）
**29、如图，已知梯形ABCD，上底AD＝12，下底BC＝28，EF∥AB分别交AD、BC于点E、F，且将梯形分成面积相等的两部分．试求BF的长．
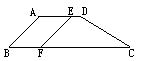
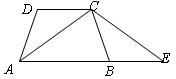
**30、如图，梯形ABCD中，AB∥CD，AD＝BC，延长AB至点E，使BE＝CD．试验证：AC＝CE．
【试题答案】
一、1、B；2、A；3、D；4、C；5、D；6、B；7、A；8、D；9、C；10、B；
二、11、1440；12、＝；13、28cm，48cm2；14、平行四边形、等腰三角形；15、40°；16、A、C、E、F、D、B（或A、C、D、F、E、B）；17、32cm；18、5cm；19、24；20、19cm，11cm,
19cm，11cm.
三、21、绕三角形一边中点旋转180°．因为旋转图形的形状、大小不变，再根据两组对边相等的四边形是平行四边形；
22、AC＝6cm，AB＝20÷4＝5(cm)，在RtΔAOB中，BO＝
＝4，BD＝2×4＝8．所以菱形面积是24cm2；
23、∠C＝∠DAB＝64°，∠D＝∠B＝116°；
24、在RtΔABD中，BD＝
＝CD，Rt△BDC中，BC＝
，ΔBDC的周长＝2
，梯形ABCD的面积＝2(2+4)÷2＝6．
25、在矩形的长的一边用80×80规格的不到8块，但要取8块才铺得整齐，宽的一边刚好6块，共8×6＝48块，需要48×40＝1920(元)；若用60×60规格的在长的一边要10块半，宽的一边要8块．共10.5×8＝84块，需要84×25＝2100(元)，故用80×80规格的好．
26、∠DFE＝15°；
27、（102－2×1×10+1×1）÷4＝20.25(米2)；
28、线段、角、等腰三角形、菱形、矩形、正方形、等腰梯形、正五边形、正六边形都是轴对称图形；线段、平行四边形、菱形、矩形、正方形、正六边形是中心对称图形；线段、菱形、矩形、正方形、正六边形既是轴对称图形又是中心对称图形（理由略）．
四、29、设BF＝x，则FC＝28－x．又设AD与BC间的距离为h，即梯形和平行四边形ABFE的BF边上的高为h．易知四边形ABFE是平行四边形，则AE＝BF＝x，DE＝12－x，由题意可得xh＝
h[(12－x)+(28－x)]．解得x＝10．即BF的长为10；
30、连结DB．说明四边形BECD是平行四边形，得DB＝CE，而AC＝BD，故AC＝CE．