【本讲教育信息】

一. 教学内容：

1. 正切函数的图象和性质

2. 函数y=Asin（ωx+φ） （A>0且A¹1，ω>0） 的图象

3. 三角函数的应用

［教学目标］

1. 理解并掌握作正切函数图象的方法，能用正切函数的图象解最简三角不等式；

2. 会用“五点法”画y＝Asin（ωx＋）的图象；

3. 理解振幅变换和周期变换和平移变换；会用图象变换的方法画y＝Asin（ωx＋）的图象；

4. 会求一些函数的振幅、周期、最值等。

［教学过程］

一、正切函数的图象和性质

1. 正切函数图象的作法

在的区间作出它的图象

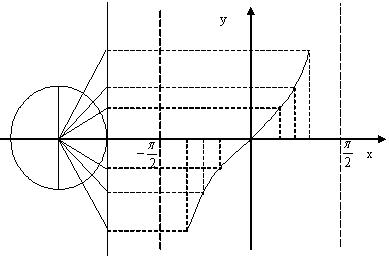
，且的图象，称“正切曲线”

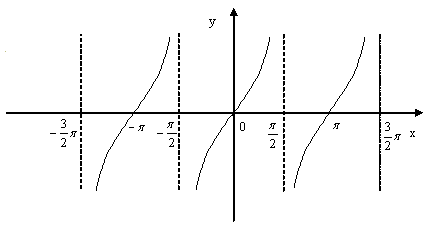
正切函数的性质：

1. 定义域：

2. 值域：R

3. 当时，当时

4. 周期性：

5. 奇偶性：奇函数

6. 单调性：在开区间内，函数单调递增

二、函数y=Asin（ωx+φ） （A>0且A¹1，ω>0） 的图象

（一）函数图象的三种变换

1. 振幅变换y=Asinx，xÎR（A>0且A¹1）的图象可以看作把正弦曲线上的所有点的纵坐标变为原来的A倍而得到。A称为振幅（物体振动时离开平衡位置的最大距离）。

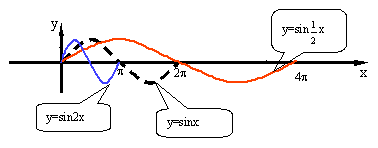
2. 周期变换:函数y=sinωx，xÎR（ω>0且ω¹1）的图象，可看作把正弦曲线上所有点的横坐标变到原来的倍（纵坐标不变）。ω决定了函数的周期。

3. 相位变换: 函数y＝sin（x＋），x∈R（其中≠0）的图象，可以看作把正弦曲线上所有点向左（当＞0时）或向右（当＜0时）平行移动｜｜个单位长度而得到。

【典型例题】

例1. 比较与的大小

解：，，

又内单调递增，

例2. 求函数的定义域、值域，并指出它的周期性、奇偶性、单调性

解：由得，

所求定义域为

值域为R，周期，是非奇非偶函数

在区间上是增函数

例3. 观察正切曲线写出满足下列条件的x的值的范围：tanx＞0

解：画出y＝tanx在（－，）上的图象，不难看出在此区间上满足tanx＞0的x的范围为：0＜x＜

结合周期性，可知在x∈R，且x≠kπ＋上满足的x的取值范围为

（kπ，kπ＋）（k∈Z）

例4. 画出函数y＝3sin（2x＋），x∈R的简图

解：（五点法）由T＝，得T＝π

列表：

X	–
2x+	0		π		2π
3sin（2x+）	0	3	0	–3	0

描点画图：

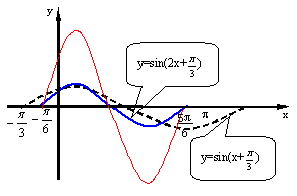
这种曲线也可由图象变换得到：

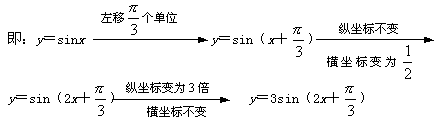
例5. 已知函数y＝Asin（ωx＋），在同一周期内，当x＝时函数取得最大值2，当x＝时函数取得最小值－2，则该函数的解析式为（ ）

A. y＝2sin（3x－） B. y＝2sin（3x＋）

C. y＝2sin（＋） D. y＝2sin（－）

解析：由题设可知，所求函数的图象如图所示，点（，2）和点（，－2）都是图象上的点，且由“五点法”作图可知，这两点分别是“第二点”和“第四点”

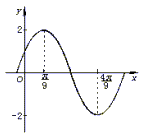
所以应有：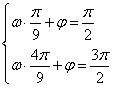

解得：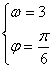

答案：B

例6. 一半径为3 m的水轮如图所示，水轮圆心O距离水面2 m，已知水轮每分钟转动4圈，如果当水轮上P点从水中浮现时（图中P₀点）开始计算时间。
（1）求P点相对于水面的高度z（m）与时间t（s）之间的函数关系式；
（2）P点第一次到达最高点大约要多长时间？

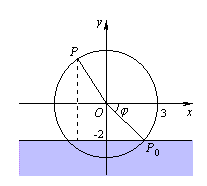
解：（1）设z=Asin（ωt+φ） +k

由题意，知，

又当t=0时，z=0，可得

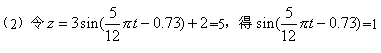
取=，解得

故点P第一次到达最高点大约需要5.5s

【模拟试题】（答题时间：30分钟）

1. 判断正误

①y＝Asinωx的最大值是A，最小值是－A

②y＝Asinωx的周期是

③y＝-3sin4x的振幅是3，最大值为3，最小值是-3

2. 下列变换中，正确的是

A. 将y＝sin2x图象上的横坐标变为原来的2倍（纵坐标不变）即可得到y＝sinx的图象

B. 将y＝sin2x图象上的横坐标变为原来的倍（纵坐标不变）即可得到y＝sinx的图象

C. 将y＝-sin2x图象上的横坐标变为原来的倍，纵坐标变为原来的相反数，即得到y＝sinx的图象

D. 将y＝-3sin2x图象上的横坐标缩小一倍，纵坐标扩大到原来的倍，且变为相反数，即得到y＝sinx的图象

3. 函数y＝tan（ax＋）（a≠0）的最小正周期为（ ）

4. 函数y＝＋的定义域是（ ）

A. （2k＋1）π≤x≤（2k＋1）π＋，k∈Z

B. （2k＋1）π＜x＜（2k＋1）π＋，k∈Z

C. （2k＋1）π≤x＜（2k＋1）π＋，k∈Z

D. （2k＋1）π＜x＜（2k＋1）π＋或x＝kπ，k∈Z

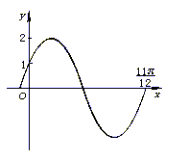
5. 已知如图是函数y＝2sin（ωx＋）其中｜｜＜的图象，那么（ ）

A. ω＝，＝ B. ω＝，＝－

C. ω＝2，＝ D. ω＝2，＝－

6. 函数y＝tan（2x＋）的图象被平行直线 隔开，与x轴交点的坐标是_________。与y轴交点的坐标是_________________，周期是__ _，定义域的集合是_______________，值域的集合是 ，它是 。

7. 已知函数y＝Asin（ωx＋）（A＞0，ω＞0，0＜＜2π＝图象的一个最高点是（2，），由这个最高点到相邻最低点的图象与x轴交于点（6，0），试求函数的解析式。

8. 如何用图象变换的方法在同一坐标系内由y＝sinx的图象画出函数y＝－sin（－2x）的图象。

9. 如图，某地一天从6时到14时的温度变化曲线近似满足函数y=Asin（ωx+φ）+B。

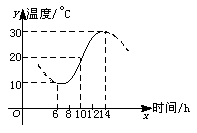
（1）求这段时间的最大温差；

（2）写出这段曲线的函数解析式。

10. 作出函数y＝｜tanx｜的图象，并观察函数的最小正周期和单调区间。

【参考答案】

1. ①（×） ②（×） ③（√）

2. A

3. C

4. C

5. C

6. （0，1）

R 非奇非偶函数

7. 解：由已知可得函数的周期T＝4×（6－2）＝16

∴ω＝＝

又A＝ ∴y＝sin（x＋）

把（2，）代入上式得：＝sin（×2＋）·

∴sin（＋）＝1，而0＜＜2π ∴＝

∴所求解析式为：y＝sin（x＋）

8. 解：∵y＝－sin（－2x）＝sin2x

作图过程：

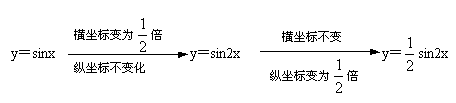
9. 解：（1）由图可知，这段时间的最大温差是30-10=20（℃）

（2）图中从6时到14时的图象是函数y=Asin（ωx+φ）+B的半个周期的图象。

∴·=14-6ω=

又由图可得

∴y=10sin（x+φ）+20

将x=6，y=10代入上式得：sin（π+φ）=-1

∴

故所求的解析式为

y=10sin（x+π）+20，x∈［6，14］

10. 函数y＝｜tanx｜的图象如下图：

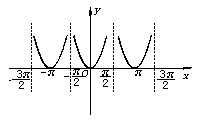
函数y＝｜tanx｜的最小正周期为π

单调递增区间为［kπ，＋kπ］，k∈Z

单调递减区间为（－＋kπ，kπ），k∈Z