【本讲教育信息】

一. 教学内容：

1. 理解多边形的有关概念；掌握多边形的内、外角和，能利用多边形的内、外角和的性质进行有关的计算．

2. 理解什么是平面图形的镶嵌以及镶嵌的原理，并能灵活运用多边形的内角和及外角和进行多种方案的镶嵌．

二. 知识要点：

1. 多边形的有关概念

（1）由一些不在同一直线上的线段首尾顺次相接组成的平面图形叫做多边形．这里所说的多边形是指凸多边形，即多边形总在任何一条边所在直线的同一侧．在平面内，内角都相等，各边都相等的多边形叫做正多边形．

（2）n边形的内角和等于（n－2）×180°．

（3）在一个多边形的每个顶点处取这个多边形的一个外角，它们的和叫做这个多边形的外角和．多边形的外角和等于360°．

2. 平面图形的镶嵌

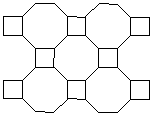
（1）用一种或几种形状、大小相同的平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，就叫做平面图形的镶嵌，也叫做平面图形的密铺．

（2）事实上，如果拼接某种多边形时，能在每个拼接点处恰好拼成平角或周角，那么用这种多边形就可以进行镶嵌．

三. 重点难点：

重点是多边形的内角和与外角和的性质及其应用以及正多边形的密铺．难点是对内角和性质的推导所利用的分割化归的思想的理解以及用多种方案进行密铺．

【典型例题】

例1. （1）n（n≥3）边形有__________条对角线．

（2）一个凸多边形的内角中，至多有__________个锐角．

分析：（1）n（n≥3）边形从一个顶点出发可引出（n－3）条对角线，n个顶点有n（n－3）条．其中每条对角线都重复了一次，故n（n≥3）边形共有对角线n（n－3）条．（2）由于凸多边形的外角和为360°，如果有4个锐角，那么这些内角的外角就有4个钝角，其和大于360°，所以有4个以上的锐角是不可能的，最多有3个锐角．

解：（1）n（n－3）（2）3．

评析：（1）计算n（n≥3）边形的对角线条数时，往往忘记重复的对角线，错答为n（n－3）条．（2）应重视多边形外角和等于360°这一隐含条件，利用同一顶点上内外角互补这一关系可以解决很多问题．

例2. 如图所示，一个正三角形经过变换依次成为正六边形、正十二边形、正二十四边形、……，当这些正多边形的周长都相等时，正六边形的面积__________正十二边形的面积（填不等符号）．

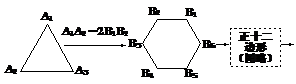
分析：周长一定的图形，圆的面积最大，由题意知在图形的变换过程中，周长不变，形状越来越接近圆形，即面积越来越大．故周长相等时，正六边形的面积小于正十二边形的面积．

解：＜

评析：细心观察，发现图形变换的规律趋势．

例3. （1）如图，有一底角为35°的等腰三角形纸片，现过底边上一点，沿与底边垂直的方向将其剪开，分成三角形和四边形两部分，则四边形中，最大角的度数是__________．

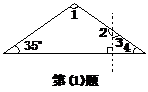
（2）若一个多边形的内角和等于720°，则这个多边形的边数是（ ）

A. 5               B. 6               C. 7               D. 8

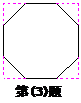
（3）将一个边长为1的正八边形补成如图所示的正方形，这个正方形的边长等于__________（结果保留根号）．

分析：（1）因为这是一个等腰三角形，所以∠4＝35°，∠1＝180°－2×35°＝110°．∠2＝90°＋∠4＝125°，在剪成的四边形中四个内角的度数分别是35°、110°、125°、90°，所以最大角的度数是125°．（2）根据多边形内角和公式（n－2）·180°＝720°，解得，n＝6，故选B．（3）设所补直角三角形的边长为a，则a²＋a²＝1²，

解：（1）125°（2）B 

例4. （1）某商店出售下列四种形状的地砖：①正三角形；②正方形；③正五边形；④正六边形．若只选购其中一种地砖镶嵌地面，可供选择的地砖共有（ ）

       A. 4种    B. 3种    C. 2种    D. 1种

（2）如下左图所示的图案是由正六边形密铺而成，黑色正六边形周围第一层有六个白色正六边形，则第n层有__________个白色正六边形．

分析：（1）能够进行平面图形镶嵌的条件是在每个拼接点处恰好拼成平角或周角．正三角形的每个内角是60°，360°÷60°＝6，即用6个正三角形可以铺成一个周角；正方形的每个内角是90°，360°÷90°＝4，即用4个正三角形可以铺成一个周角；正五边形的每个内角是108°，360°÷108°＝即用正五边形不能正好铺成一个周角，所以不能用来镶嵌；正六边形的每个内角是120°，360°÷120°＝3，即用3个正六边形可以铺成一个周角．（2）根据图形排列找规律，方法很多．如：把一层白色正六边形的中心连起来，在得到的六边形中，每边上的六边形个数是2，共有六边形2×6－6＝（2－1）×6＝1×6；第二层做同样处理，六边形共有3×6－6＝（3－1）×6＝2×6；按照这样的规律，第n层有n×6＝6n个．

解：（1）B（2）6n

例5. 如图（1）所示是用12个全等的等腰梯形镶嵌成的图形，这个图形中等腰梯形的上底长与下底长的比是__________．

分析：如图（2）所示，∠1＝∠2＝∠3，∠1＋∠2＋∠3＝360°，所以3∠1＝360°，即∠1＝120°．所以梯形的上底角均为120°，下底角均为60°．由于EF即是梯形的腰，又是梯形的上底，所以梯形的腰等于上底．连结MN，则∠FMN＝∠FNM＝因此，梯形的上底等于下底的一半．

解：1∶2

评析：本题综合考查了密铺、等腰梯形、等腰三角形、直角三角形等知识．通过观察图形，发现腰等于上底十分关键．

例6. 已知：如图（1）所示，现有a×a，b×b的正方形纸片和a×b的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使拼出的矩形的长和宽分别为a＋2b和2a＋b．

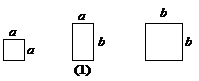
分析：此题为开放题，答案不唯一．

解：如图（2）所示．

评析：图中同一行或同一列的均可变换位置，构成新的拼图．

【方法总结】

1. 在应用多边形的内角和、外角和进行有关的计算时，要注意用方程的思想或是不等式的思想来解决问题．

2. 本讲学习了平面图形的镶嵌（密铺），掌握同种多边形及多种多边形密铺的方法（同一顶点内角和为360°）．

【模拟试题】（答题时间：60分钟）

一. 选择题

1. 一个多边形内角和是1080°，则这个多边形是（ ）

A. 六边形             B. 七边形            C. 八边形               D. 九边形

2. 当凸多边形的边数由3增加到n时，其外角度数的和（ ）

A. 增加                 B. 减少               C. 保持不变           D. 变成（n－3）×180°

3. 只用下列图形不能镶嵌的是（ ）

A. 三角形             B. 四边形            C. 正五边形           D. 正六边形

4. n边形的n个内角中，锐角的个数最多有（ ）

A. 1个                   B. 2个                 C. 3个                    D. 4个

5. 边长为a的正六边形的面积等于（ ）

6. 一定不能够进行组合镶嵌的是（ ）

A. 正六边形与正三角形                   B. 正八边形与正方形

C. 正三角形与正方形                       D. 正五边形与正七边形

7. 如果在一个顶点周围用两个正方形和n个正三角形恰好可以进行平面镶嵌，则n的值是（ ）

A. 3                       B. 4                     C. 5                        D. 6

**8. 一个凸多边形截去一个角后形成的多边形的内角和是2520°，则原多边形的边数是（ ）

A. 14                     B. 15                   C. 15或16              D. 15或16或17

二. 填空题

1. __________边形的内角和等于它的外角和的6倍．

2. 从八边形的一个顶点出发，可作__________条对角线．

3. 一个多边形的每一个外角等于72°，则这个多边形是__________边形，它的每一个内角是__________度．

4. 两个多边形恰好能拼成一个四边形，则这个多边形__________进行镶嵌．

5. 任意四边形都能密铺，每个拼接点处的四个角恰好是一个四边形的__________，它们的和是__________度．

6. 若多边形的每一个内角都是150°，那么这个多边形是__________边形．

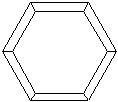
7. 如图，用6个全等的等腰梯形纸板不重叠不留空隙地拼成一个边框为正六边形的纸环，则等腰梯形的四个角中最小的角为__________．

三. 解答题

1. 如果一个n边形的每一个内角都相等，且它的每一个外角与一个内角的比为2∶3，求这个n边形的内角和．

2. 小美想：2008年奥运会在北京召开，设计一个内角和是2008°的多边形图案多好，小美的想法能实现吗？若能，请画出；若不能，请说明理由．

3. 某种机器人每前行1m就向左转30°，它需要走多少米才能回到原地？

*4. 小方家购买一套新房，卫生间只有4m²，他家已有正六边形地砖16块，每块地砖的面积为请问这16块地砖装修卫生间地面够吗？若够怎么铺？请你设计出草图．（地砖可以分割）

**5. 从正三角形、正四边形、正六边形中选一种，再在其他正多边形中选一种，请画出用这两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形？说明你的理由．

【试题答案】

一. 选择题

1. C  2. C  3. C  4. C  5. C  6. D  7. A  8. D（提示：截一个角有三种可能，如图所示．）

二. 填空题

1. 十四  2. 5  3. 五，108°  4. 能  5. 四个角，360°  6. 十二  7. 60°

三. 解答题

1. 因为一个外角与一个内角的和是180°，所以一个内角是180°×＝108°，由（n－2）·180°＝n·108°，所以n＝5．所以108°×5＝540°．即这个n边形的内角和是540°．

2. 小美的想法无法实现．因为多边形的内角和（n－2）×180°一定是180°的整数倍，而2008不能被180整除，所以不可能有内角和为2008°的多边形．

3. 机器人走的正多边形的边数为360÷30＝12，这个正多边形的周长为1×12＝12（m）．即它需要走12m才能回到原地．

4. 这16块砖恰好够装修卫生间，如图所示：（正六边形可以分割后，再平移到相应的位置．）

5. 如正方形和正八边形，如图所示，设在一个顶点周围有m个正方形的角，n个正八边形的角，那么m、n应是m·90°＋n·135°＝360°的正整数解，即2m＋3n＝8的正整数解．因为这个方程的正整数解只有一组，所以符合条件的图形只有一种．