【本讲教育信息】
一. 教学内容：
37投影与视图
1. 平行投影和中心投影．
2. 简单几何体的三视图．
3. 几何体的平面展开图及其应用．
二. 知识要点：
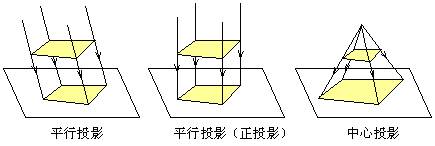
1. 平行投影
（1）物体在光线的照射下，会在地面上或墙面上留下它的影子，这种现象就是投影．
（2）太阳的光线可看做是平行的，像这样的光线照射在物体上，所形成的投影叫做平行投影．光线是投影线，地面或墙面是投影面．
（3）在平行投影中，光线是竖直照射在水平面上的．像这种平行投影又叫做正投影．
2. 中心投影
蜡烛、白炽灯的光线可以看做是从一点发出的，像这样的光线照射在物体上所形成的投影，叫做中心投影．
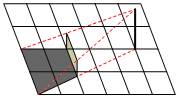
3. 视点、视线、盲区
眼睛所在的位置叫做视点，由视点发出的线叫做视线，看不到的地方叫做盲区．
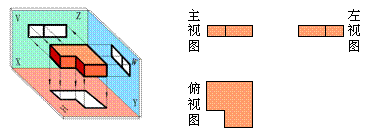
4. 三视图
（1）物体的正投影叫做物体的视图．从正面得到的视图叫做主视图，从上面得到的视图叫做俯视图，从左面得到的视图叫做左视图．主视图、俯视图、左视图，三者合在一起叫做三视图．
（2）在物体的三视图中，主视图可反映出物体的长和高，俯视图可反映出物体的长和宽，左视图可反映出物体的高和宽．三视图的摆放位置一般是：俯视图在主视图的下面，左视图在主视图的右面．
5. 几何体的展开图及其应用
6. 知识结构
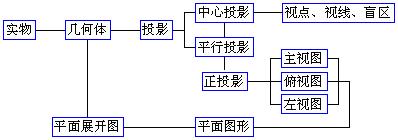
三. 教学重、难点：
重点内容是平行投影、中心投影、三视图，以及简单几何体的平面展开图．难点是平行投影和中心投影的区别和联系，投影和三视图的实际应用．
四. 考点分析：
在近两年的中考中，有关三视图及投影知识的题目是必考内容，常常以填空、选择、作图题的形式出现，一般难度为中等或中等偏下．而且中考对本章的要求逐渐提高，新的题型不断出现，有关知识与实际问题相结合是今后中考命题的方向．
【典型例题】
例1. （1）同一时刻，两根长度不等的竿子置于阳光之中，如果它们的影长相等，那么这两根竿子的相对位置是（ ）
A．两根都垂直于地面 B．两根平行地斜插在地上
C．两根竿子不平行 D．一根倒在地上
（2）下列物体的影子，不正确的是（ ）
分析：（1）长度不相等，若平行放置，则影子不相等，故A、B排除，D表达不明确．故应选C．（2）A．太阳光线是平行的，故影长与物体高度成正比例，所以A正确．B．太阳光线画得不平行，故B错．C．因为物体在光源两侧，故影子方向不同，因而C正确．D．因灯光是发散的，故影长与物体高度不成比例且物体在光源同侧，影子方向相同，D正确．
解：（1）C（2）B
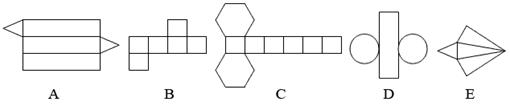
例2. 下列四个图形中，经过折叠可以围成一个棱柱的是（ ）
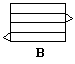
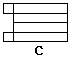
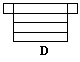
分析：先想后折是对空间观念的一个培养过程，A、B项中多边形边数与小长方形个数不相符；C项中两个多边形都在长方形的一侧，只有D项能折成棱柱．
解：D
例3. （1）数学课外活动小组为测量旗杆AB的高，在同一时刻、测得一杆EF的高为
A．
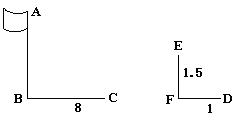
（2）下列说法正确的有（ ）
①一个物体在灯光的照射下，其影子的大小、方向与灯的位置有关；
②物体在阳光照射下其影子只与物体的高度有关；
③俗话说：“站得高，看得远”，说明在高处盲区小；
④我们在坐车向前行驶时，有时会发现一些高大的建筑物被较矮的建筑物挡住了．
A．1个 B．2个 C．3个 D．4个
分析：（1）在同一时刻，物高与影长成比例，由此可得：
∴AB＝12（米）．（2）其中②错误，影长除与物体高度有关外，与照射时间也有关．
解：（1）B（2）C
例4. 某工厂要加工一批密封罐，设计者给出了密封罐的三视图（如下图），请你按照三视图确定制作每个密封罐所需钢板的面积．
（单位：mm）
分析：对于某些立体图形，若沿其中一些线（例如棱柱的棱）剪开，可以把立体图形的表面展开成一个平面图形——展开图．在实际的生产中，三视图和展开图往往结合在一起使用．解决本题的思路是，由视图想象出密封罐的立体形状，再进一步画出展开图．从而计算面积．
解：由三视图可知，密封罐的形状是正六棱柱，如图（左）．密封罐的高为
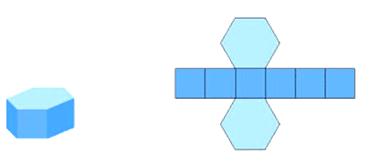
由展开图可知，制作一个密封罐所需钢板的面积为：
≈27990（mm2）．
例5. 如图所示，直角坐标平面内，小聪站在x轴上的点A（－10，0）处观察y轴．眼睛距地面
（1）盲区在y轴上的范围；
（2）盲区的面积．
分析：（1）盲区的范围是线段EF，只要求出点E、F的坐标即可，由△ABD≌△OFD，可得OF＝AB，从而得到点F的坐标，进而由EO＝EF－OF求出点E的坐标．（2）盲区是梯形CDFE，它的面积可由S△BEF－S△BCD求得．
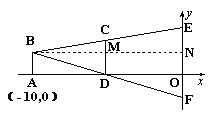
解：（1）如图，过点B作BN⊥y轴交CD于点M，垂足为点N，
因为CD∥y轴，所以BM⊥CD．∠BCD＝∠BEF，∠BDC＝∠BFE，
所以△BCD∽△BEF．
解得EF＝
因为AD＝OD，∠BDA＝∠FDO，∠BAO＝∠FOD，所以△ABD≌△OFD．
所以AB＝OF＝
所以EO＝EF－OF＝4－1＝
所以E（0，3），F（0，－1）．
答：盲区在y轴上的范围是E（0，3）至F（0，－1）之间．
S梯形CDFE＝S△BEF－S△BCD＝20－5＝
答：盲区面积为
【方法总结】
1. 在阳光下，两根长度不同的标杆直立在地面上，其影子或在一条直线上或是平行的；标杆、影子及过杆顶的光线构成的两个直角三角形相似．在点光源的照射下，两根直立在地面上的标杆形成的影子一般是不平行的．两根标杆顶端和它们影子顶端的两条连线的交点处，即是点光源所处的位置．
2. 在画三视图时，看得见的轮廓线要画成实线，看不见的轮廓线要画成虚线．三视图的摆放位置一般是：在主视图下面是俯视图，主视图右面是左视图，且主、俯视图上下对正，主、左视图高度一致，俯视图和左视图的宽度一致．
【预习导学案】
（复习一：实数）
一. 预习前知
1. 什么叫有理数，有理数如何分类？
2. 实数是如何分类的？
二. 预习导学
1. 借助数轴理解相反数和绝对值的意义，︱a︱＝．
2. 如何借助数轴比较实数的大小？
3. 什么是平方根、算术平方根、立方根？
4. 实数的运算律和运算法则是怎样的？
反思：（1）数系扩张后，体会实数的性质和运算规律．
（2）学习实数引入了一个非常重要的工具——数轴，想一想数轴的作用．
【模拟试题】（答题时间：50分钟）
一. 选择题
1. 下列关于圆柱三种视图的说法正确的是（ ）
A．圆柱的主视图一定是矩形 B．圆柱的左视图一定为矩形
C．圆柱的俯视图一定为圆 D．圆柱的主视图可能为矩形也可能为圆
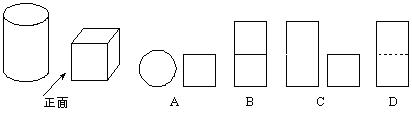
2. 如图，小明从正面观察一个圆柱体邮筒和一个正方体箱子，看到的是（ ）
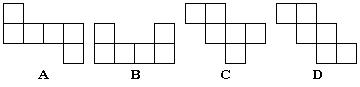
3. 下列图形中，不能经过折叠围成正方体的是（ ）
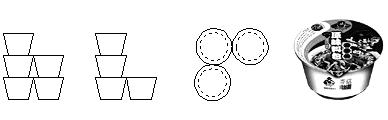
4. 若干桶方便面摆放在桌子上，实物图片左边所给的依次是它的主视图、左视图和俯视图，则这一堆方便面共有（ ）
A．5桶 B．6桶 C．9桶 D．12桶
5. 如图所示，爸爸、妈妈和小华到郊外游玩，爸爸在地上画出同一时刻妈妈和小华以及她们在地上的影子的4幅图．请你判断小华爸爸画的图正确的是（ ）
**6. 如图所示，把一个正方体以顶点朝上正放，若此时正方体的上方有一盏灯，则该正方体在桌面上的影子是（ ）
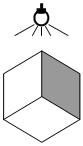
A．三角形 B．正方形 C．长方形 D．六边形
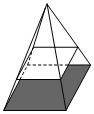
*7. 如图所示，方桌正上方的灯泡（看作一个点）发出的光线照射方桌后，在地面上形成阴影（正方形），已知方桌的边长是
A．
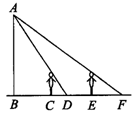
**8. 如图，王华晚上由路灯A下的B处走到Ｃ处时，测得影子CD的长为
A．
二. 填空题
1. 画三视图是有一定要求的：俯视图在主视图的__________，左视图在主视图的__________，主视图反映物体的__________，俯视图反映物体的__________，左视图反映物体的__________．
2. 晚上，在小明的房间里小明和爸爸玩将手影投在墙上的游戏，爸爸的手大，手影做出了一只小狗，小明的手小，但其手影却做出了一只更大的狗，则小明的手比爸爸的手__________墙．（填“靠近”或“远离”）
3. 某学校乘租用的汽车去旅游，小华坐在第一排，小明坐在第三排，如果俩人同时向前看去，则__________的盲区大些．
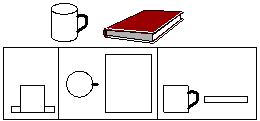
4. 如图所示，桌上放着一个杯子和一本书，则下列三个视图从左到右依次是__________视图，__________视图和__________视图．
5. 如图，已知李明的身高为
**6. 如图是由一些相同的长方体积木块搭成的几何体的三视图，则此几何体共由________块长方体积木搭成．
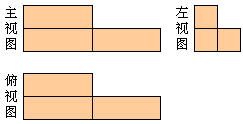
三. 解答题
1. 坐在后排的小李被前排的小张的头挡住了，看不见黑板．小李心中不悦，半开玩笑地说：“小张，你的头比黑板还大，黑板都被你挡住了，我一点也看不见！”同学们，小李的这种说法正确吗？只有大的东西才会挡住小的东西而使人看不见吗？
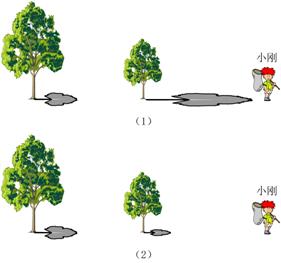
2. 如图，分别是两棵树及其影子的情形
（1）哪个图反映了阳光下的情形？哪个图反映了路灯下的情形？
（2）你是用什么方法判断的？
（3）请你画出图中表示小刚影长的线段．
*3. 如图，花丛中有一路灯杆AB在灯光下，小明在D点处的影长DE＝
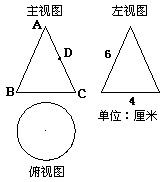
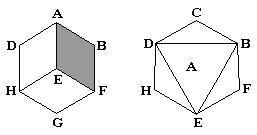
**4. 如图是一个几何体的三视图．（1）写出这个几何体的名称；（2）根据所示数据计算这个几何体的表面积；（3）如果一只蚂蚁要从这个几何体中的点B出发，沿表面爬到AC的中点D，请你求出这个线路的最短路程．
【试题答案】
一. 选择题
1. D【圆柱如果竖直放置，主视图和左视图是矩形，俯视图是圆；如果“倒着”放，则其三视图不确定】
2. C【看到的是圆柱体的主视图和正方体的主视图】
3. B
4. B
5. C【他们到郊外游玩，其影子是太阳光形成的平行投影．所以她们的影子应该在同一方向上，所以B、D错误．同一时刻物高和影长成正比，所以C正确．】
6. D【其投影各点之间的对应关系如图所示】
7. A【根据题意可得方桌与其阴影的面积比等于灯泡到方桌的距离与灯泡到地面的距离之比的平方】
8. B【根据题意可得
因为CD＝1，EF＝2，BF＝BD＋CD＋DE＋EF＝BD＋4．解得AB＝6．在解答相似三角形的有关问题时，遇到有公共边的两对相似三角形，往往会用到中介比，它是解题的桥梁，如该题中的
】
二. 填空题
1. 下面，右面，长和高，长和宽，高和宽
2. 远离
3. 小明
4. 左，俯，主
x＝
6. 4【由左视图可知这堆木块有两层，由俯视图可知底层有三块，由左视图和俯视图可知上面一层只有一块，共4块】
三. 解答题
1. 不正确，小李的视线被较近的物体－小张的头挡住了．因此黑板成为小李向前看的盲区．所以小李才会看不见黑板，较小的物体离眼睛较近时，会给人形成较大的盲区．
2. （1）第一幅图是路灯灯光形成的，第二幅图是太阳光形成的（2）太阳光是平行光线，物高与影长成正比（3）画图略
3. 根据题意，△CDE∽△ABE，△FGH∽△ABH，则
因为CD＝FG＝1.7，DE＝3，DG＝5，GH＝5，所以
从而解得AB＝5.95≈6.0（米）
4. （1）圆锥（2）由左视图可知，底面圆的直径是4厘米，半径是2厘米，母线长为6厘米，则侧面积为12π平方厘米，底面面积为4π平方厘米，表面积为16π平方厘米（3）这个圆锥的侧面展开图如图所示，由图中数据可得其圆心角为120°．则∠BAC＝∠B’AC＝60°，连结BC，则△ABC是等边三角形，点D是AC的中点，所以BD⊥AC，且BD平分AC，BD的长就是所求的最短距离．
厘米．
