![]()
课程解读
一、学习目标:
1. 认识长方体和正方体,了解各部分的名称和特点。
2. 掌握长方体、正方体的棱长和公式。
3. 进一步培养学生的空间想象能力和探索意识。
二、重点、难点:
重点:长方体和正方体各部分的名称和特点。
难点:利用长方体、正方体的棱长和公式解决实际问题。
三、考点分析:
1. 本讲知识以填空、选择题的形式出现,考查对长方体和正方体各部分的名称、特点棱长及和公式的理解。
2. 以应用题的形式出现时,多是利用对长方体、正方体的棱长和公式解决实际问题。
3. 本讲内容在考试中的分值多在8分左右。
知识梳理
|
|
相同点 |
不同点 |
|||
|
|
面 |
棱 |
顶点 |
面 |
棱 |
|
长方体 |
6 |
12 |
8 |
6个面都是长方形(有时也有两个相对的面是正方形),相对的面完全相同。 |
相对的棱长度相等。 棱长和=(长+宽+高)×4 |
|
正方体 |
6 |
12 |
8 |
6个面都是完全相同的正方形。 |
每条棱的长度都相等。 棱长和=棱长×12 |
典型例题
方法应用题:
例1. 标出下图中长方体的长、宽、高和正方体的棱长。
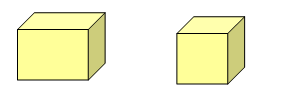
思路分析:
1)题意分析:本题考查对长方体和正方体各部分名称的理解。
2)解题思路:
在长方体中,左右方向的棱是长,前后方向的棱是宽,上下方向的棱是高。
在正方体中,每条边都是棱长。
解答过程:
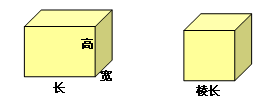
解题后的思考:这是一道基础题,要理解长方体中的长、宽、高各是哪条边。
例2. 一个长方体中最多有( )个面是相同的。
思路分析:
1)题意分析:本题主要考查对长方体中面的理解。
2)解题思路:要知道最多有几个面相同,首先得明白面特点:6个面,相对的面完全相同。思考后发现,最多有两组相对的面完全相同。
解答过程:一个长方体中最多有( 4 )个面是相同的.
解题后的思考:本题的重点是理解面的特点,容易出错的地方是想成6个,那就变成正方体了。
例3. 求下面长方体的棱长和。

思路分析:
1)题意分析:这道题是对长方体棱长和的练习。
2)解题思路:理解棱长和的计算公式,直接利用公式就能解决问题。
解答过程:
(5+4+3)×4
=12×4
=48(厘米)
解题后的思考:本题考查对长方体棱长和的掌握,最后写单位名称时要注意是长度单位。
例4. 下面哪个图形能围成长方体?

思路分析:
1)题意分析:此题要想象出长方体的展开图。
2)解题思路:判断平面展开图折叠后是否能围成长方体(或正方体):
规律是:平面展开图中有4个长方形(或正方形)连成一排时,另外两个长方形(或正方形)一定在这一排长方形(或正方形)的两侧(注意相对的面完全相等)。
想象:把其中的一个图形作为底,将其他的图形围绕着这个底面折一折,如果有重合的面或相对的面大小不相等,就不能围成长方体(或正方体)。
解答过程:
能围成长方体的图形有①、③、⑤、⑥。
解题后的思考:此题考查对展开图的理解,一定要掌握判断的方法。
例5. 一个正方体的6个面上分别写着六个字母,根据下图摆放的三种情况,判断每个字母对面上的字母分别是什么?
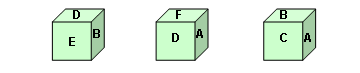
思路分析:
1)题意分析:本题需要有空间想象力,知道在长方体或正方体中每一个面都有四个相邻的面。
2)解题思路:由前两种摆放情况可看出:D与E、B、F、A四个面相邻,所以肯定和C相对;由后两种摆放情况可看出:A与F、D、B、C相邻,那它只能与E相对;剩下的B和F相对。
解答过程:A的对面是E,B的对面是F,C的对面是D。
解题后的思考:面对这样的题,有的学生可能弄不清面与面的关系,所以一定要掌握做题的方法。
综合运用题:
例6. 一个长方体的长、宽、高分别是
思路分析:
1)题意分析:本题考查长方体和正方体的棱长和。
2)解题思路:长方体的棱长和=(长+宽+高)×4;
正方体的棱长和=棱长×12。
根据条件先求出长方体的棱长和,再除以12就是正方体的棱长。
解答过程:(5+4+3)×4=12×4=48(厘米)
48÷12=4(厘米)
答:这个正方体的棱长是4厘米。
解题后的思考:本题的难点是理解公式,及计算准确。
例7. 把两个棱长都是
思路分析:
1)题意分析:本题是由正方体的棱长求长方体的棱长和。
2)解题思路:先画出示意图,再分析。

两个正方体拼成长方体后,长是
解答过程:3×2=6(厘米)
(6+3+3)×4=12×4=48(厘米)
答:拼成的长方体的棱长和是
解题后的思考:这道题中的图形要能想象出来,根据公式解题时要认真,细心。
思维突破题
例8. 一个长方体纸盒的长是宽的3倍,宽比高少
思路分析:
1)题意分析:这道题还是对长方体棱长和公式的应用。
2)解题思路:根据长与宽,宽与高的关系,可以利用方程来解答。
解答过程:设长方体纸盒的宽是x厘米。
(3x+x+x+5)×4=100
(5x+5) ×4=100
5x+5=100÷4
5x+5=25
5x=25-5
5x=20
x=20÷5
x=4
长:4×3=12(厘米) 高:4+5=9(厘米)
答:它的长是
解题后的思考:本题是利用方程的方法解题,关键是用字母表示出长、宽、高。
提分技巧
1. 掌握长方体和正方体各部分的名称和特点,理解棱长和公式。
2. 要有空间想象力,擅于把图形和文字结合。
预习导学
这节课,我们认识了长方体和正方体,知道了它们的特点,利用棱长和公式解决了很多问题,下节课,我们继续学习长方体和正方体的表面积。
一、预习新知
长方体、正方体各部分的名称和表面积。
二、预习点拨
探究与反思
探究任务一:长方体、正方体的表面积公式各是什么?
【反思】长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长×棱长×6
探究任务二:如何利用长方体和正方体的表面积公式解决实际问题。
【反思】生活中常用到表面积公式解决实际问题,所以要能灵活运用公式。
同步练习(答题时间:45分钟)
一、填空题
1. 长方体有( )个面、( )条棱、( )个顶点。
2. 正方体是特殊的( )。
3. 数学课本的形状是(
),魔方的形状是(
)。
4. 一个正方体的棱长是a分米,它的棱长和是( )分米。
5. 有一个用钢筋焊接而成的长方体形状的广告牌,长
二、选择题
1. 长方体相邻的两个面的面积相比较,( )相等。
A. 一定 B. 一定不 C. 不一定
2. 长方体中至少有( )个面是长方形。
A. 2 B.
3. 长方体和正方体( )相等。
A. 顶点个数 B. 棱的长度 C. 面的形状
*4. 用一根长( )厘米的铁丝,正好可以做成一个长6厘米、宽5厘米、高3厘米的长方体框架。
A. 14 B.
三、解答题
1. 用一根丝带捆扎一个长25厘米、宽20厘米、高10厘米的礼品盒,结头处的丝带长40厘米,捆扎这个礼品盒至少需要多长的丝带?
2. 将1、2、3、4、5、6分别填入正方体的展开图中(如下图),使相对的面上的数字相加的和是7。

3. 一个正方体,它的6个面上的编号分别是1、2、3、4、5、6,根据下面三种摆放情况,把相对的面的编号写出来。

![]()
试题答案
一、填空题
1. 6、12、8
2. 长方体
3. 长方体、正方体
4.
5. 20
二、选择题
1. C
2. B
3. A
4. C (6+5+3)×4=14×4=56
三、解答题
1. (25+20+10)×4+40=55×4+40=220+40=260(厘米)
2. 只要和是7的两个面不相邻即可。(答案不唯一)
例如:
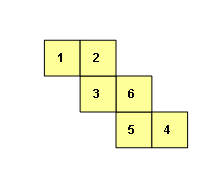
3. (1)与(4)相对; (2)与(6)相对;
(3)与(5)相对。