【本讲教育信息】

一、教学内容：

统计图表与数据的数字特征

二、学习目标

1、在表示样本数据的过程中，学会列频率分布表、画频率分布直方图、频率折线图、茎叶图，体会它们各自的特点；

2、通过实例理解样本数据标准差的意义和作用，学会计算数据标准差；

3、能根据实际问题的需求合理地选取样本，从样本数据中提取基本的数字特征（如平均数、标准差），并作出合理的解释

三、知识要点

1、频率分布表：以表格的形式给出各数据出现的频率；

2、条形统计图（频率分布直方图）：横坐标为数据范围，纵坐标为数据频数或频率或频率/组距。作频率分布直方图的方法为：把横轴分成若干段，每一段对应一个组的组距，以此线段为底作矩形，高等于该组的频率/组距，这样得到一系列矩形，每一个矩形的面积恰好是该组上的频率．这些矩形构成了频率分布直方图．

3、频率分布折线图：在频率分布直方图中，取相邻矩形上底边的中点顺次连结起来，就得到频率分布折线图（简称频率折线图）

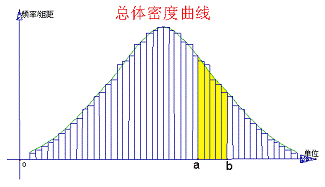
注：如果样本容量取的足够大，分组的组距取的足够小，则相应的频率折线图将趋于一条光滑的曲线，称这条光滑的曲线为总体密度曲线．

4、茎叶图：又称“枝叶图”，它的思路是将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为一个主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面的几个数，每个数具体是多少。

5、扇形图：扇形统计图是用整个圆表示总数，用圆内各个扇形大小表示各部分数量占总数的百分比数。

注：扇形统计图可以很方便地转化为饼形统计图。

6、反映数据平均取值大小（期望）的量：平均数、中位数、众数

7、反映数据稳定性大小的量：

方差（）；标准差（）；极差

四、考点解析与典型例题

考点一 画频率分布直方图

例1. 为了了解一大片经济林的生长情况，随机测量其中的100株的底部周长，得到如下数据表（长度单位：cm）：

（1）编制频率分布表；（2）绘制频率分布直方图

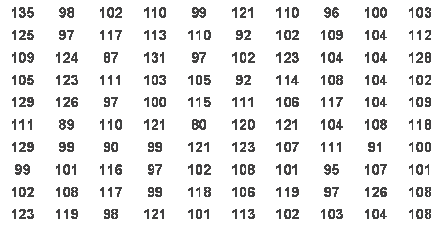
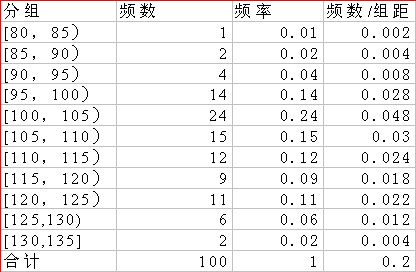
【分析】绘制频率分布直方图之前，一般地可先编制频率分布表，这样便于对数据进行分组及计算频数和频率。 分组一般以7~11组为宜。

【解】

（1）频率分布表

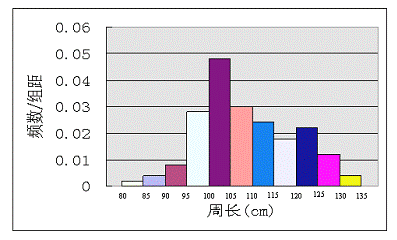
（2）频率分布直方图：

考点二：画频率（分布）折线图

例2. 如例1，试画出树林底部周长的频率分布折线图。

【分析】在频率分布直方图中，按照分组原则，在左边和右边各加一个区间，从所加的左边区间的中点开始，用线段依次连接各个矩形的顶端中点，直至右边所加区间的中点，这样得到的一条折线就是频率折线图。

【解】取[75，80]的中点作为折线的起点，以（135，140）的中点作为折线的终点，连接各矩形上底中点所得折线即为所求（如图）。

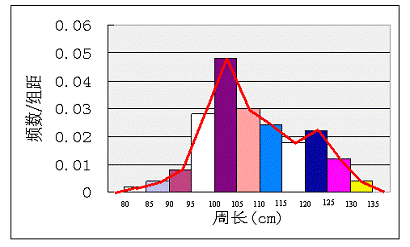
考点三 绘制茎叶图

例3. 现有甲乙两个学习小组，他们在一次测验中的成绩如下：

甲：63，66，74，79，81，82，82，82，84，85，85，86，88，91，93

乙：58，64，67，68，74，75，76，76，78，79，80，81，82，85，90

试画出测试成绩的茎叶图。

【分析】由于成绩均为两位数，且十位数字变化小而个位数字变化大，因此可以十位为“茎”，以个位为“叶”来绘制茎叶图。

【解】茎叶图如图：

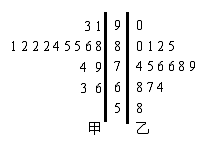
考点四 绘制扇形图

例4. 某学校高一、高二、高三年级分别有学生1000、800、700人，试画出学生数的扇形统计图。

【解】

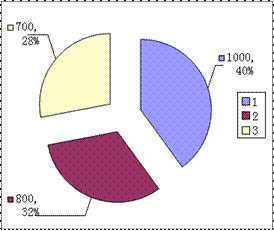
考点五 研究数据的数字特征

例5. 质检部门对甲、乙两种日光灯的使用时间进行了破坏性试验，10次试验得到的两种日光灯的使用时间如下表所示，问：两种产品的使用时间的平均值、中位数、众数、极差、标准差分别是多少？

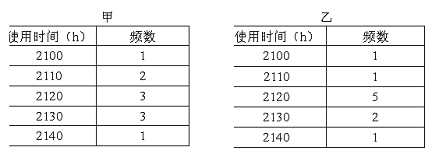
【解】平均值——甲：2121；乙：2121；

中位数——甲：2120；乙：2120；

众数——甲：2120，2130；乙：2120；

极差——甲：40；乙：40；

标准差——甲：11.972189997；乙 ：11.005049346

【注】两种产品的平均使用时长是一样的，但从标准差的结果来看，乙种产品更稳定。

五、数学思想方法

本讲主要内容是统计图表及数据的数字特征，通过对这些内容的学习，我们要学会如何合理地整理和分析数据，如何从数据中提取信息，要学会根据实际问题的需要，选择不同的方法整理数据，并从样本数据中提取需要的数字特征 ；同时，要能够体会到统计思维与确定性思维的差异并注意到统计结果的随机性。

【模拟试题】（答题时间：90分钟）

一、选择题

1. 一般情况下，用扇形图描述数据时，每部分占总体的百分比之和

A. 大于1 B. 等于1 C. 小于1 D. 不能确定

2. 频数分布直方图中长方形的高是该组数据的

A. 频率 B. 个数

C. 所占总体的百分比 D. 与该组数据无关

3. 在如图所示的茎叶图中，众数是

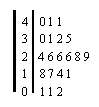
A. 1 B. 6 C. 26 D. 2

4. 在对某地区的一次人口抽样统计分析中，各年龄段（年龄为整数）的人数比例如下表所示，如用统计图表表示出来，用哪种统计图更合适

年龄段	0～9	10～19	20～49	50～79	80～
人数比例	9%	11%	52%	26%	2%

A. 直方图 B. 茎叶图 C. 扇形图 D. 折线图

5. 从某项综合能力测试中抽取100人的成绩，统计如表，则这100人成绩的标准差为

分数	5	4	3	2	1
人数	20	10	30	30	10

A. B. C. 3 D.

6. 如图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字，右边的数字表示城镇居民百户家庭人口数的个位数字，从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为

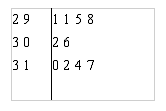
A. 304.6　　　　　 B. 303.6 C. 302.6 D. 301.6

7. 某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：第一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒；第六组，成绩大于等于18秒且小于等于19秒．右图是按上述分组方法得到的频率分布直方图．设成绩小于17秒的学生人数占全班总人数的百分比为，成绩大于等于15秒且小于17秒的学生人数为，则从频率分布直方图中可分析出和分别为（ ）

A. 0.9，35 B. 0.9，45 C. 0.1，35 D. 0.1，45

二、填空题

8. 为了调查某厂工人生产某种产品的能力，随机抽查了20名工人某天生产该产品的数量.产品数量的分组区间为，，由此得到频率分布直方图如图所示，则这20名工人中一天生产该产品数量在的人数是　　　.

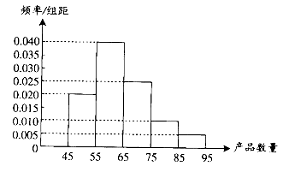
9. 已知总体的各个体的值由小到大依次为2，3，3，7，a，b，12，13.7，18.3，20，且总体的中位数为10.5．若要使该总体的方差最小，则a、b的取值分别是　　　　 ．

三、解答题

10. 某次数学测验成绩如下：

63，84，91，53，69，81，61，69，91，78，75，81，80，67，76，81，79，94，61，69，

89，70，70，87，81，86，90，88，85，67，71，82，87，75，87，95，53，65，74，77

按10分的组距分段，请画出此次学生成绩的频率分布直方图和频率折线图。

11. 甲、乙、丙三名射箭运动员在某次测试中各射箭20次，三人的测试成绩如下表

用分别表示甲、乙、丙三名运动员这次测试成绩的标准差，试求出的值。

12. 某公司在过去几年内使用某种型号的灯管1000支，该公司对这些灯管的使用寿命（单位：小时）进行了统计，统计结果如下表所示：

分组	[500，900）	[900，1100）	[1100，1300）	[1300，1500）	[1500，1700）	[1700，1900）	[1900，）
频数	48	121	208	223	193	165	42
频率

（I）将各组的频率填入表中；

（II）根据上述统计结果，计算灯管使用寿命不足1500小时的频率。

13. 在生产过程中，测得纤维产品的纤度（表示纤维粗细的一种量）共有100个数据，将数据分组如右表：

（Ⅰ）在答题卡上完成频率分布表，并在给定的坐标系中画出频率分布直方图；

（Ⅱ）估计纤度落在中的频率及纤度小于的频率是多少？

分组	频数
合计

【试题答案】

一、选择题

1. B 2. B 3. C 4. C 5. B 6. B 7. A

二、填空题

8. 13

9.

三、解答题

10. 解：

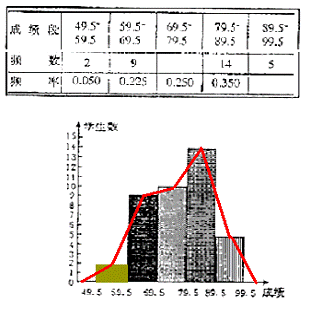
11. 解：

s1=1.1470786694

s2=1.2354415362

s3=1.0513149661

12.（I）解：

分组	[500，900）	[900，1100）	[1100，1300）	[1300，1500）	[1500，1700）	[1700，1900）	[1900，）
频数	48	121	208	223	193	165	42
频率	0.048	0.121	0.208	0.223	0.193	0.165	0.042

（II）由（I）可得，所以灯管使用寿命不足1500小时的频率为0.6．

13.（Ⅰ）

分组	频数	频率
	4	0.04
	25	0.25
	30	0.30
	29	0.29
	10	0.10
	2	0.02
合计	100	1.00

（Ⅱ）纤度落在中的频率约为，纤度小于1.40的频率约为．