![]()
【本讲教育信息】
一、教学内容:
斜抛运动的规律
二、考点点拨
本部分知识是曲线运动中运动的合成与分解的进一步应用,掌握斜抛运动的规律和应用将有利于我们解决其它曲线运动。
三、跨越障碍
(一)竖直上抛运动
物体有竖直向上的初速度且只受重力作用。
解决办法:
1、竖直上抛运动可以分为向上的匀减速直线运动和向下的自由落体运动两个过程,两个过程所用时间相同。可以分过程计算。
2、也可全过程处理,看做加速度始终为重力加速度的匀减速直线运动。
速度表达式:![]() ;上升时间
;上升时间![]()
位移表达式:![]() ;最大高度
;最大高度![]()
特别注意各矢量的正负号,一般选取向上为正方向,![]() 总是正值,上升过程中
总是正值,上升过程中![]() 为正值,下落过程中
为正值,下落过程中![]() 为负值;物体在抛出点以上时
为负值;物体在抛出点以上时![]() 为正,物体在抛出点以下时
为正,物体在抛出点以下时![]() 为负;在抛出点以上时,一个位移对应两个不同的时刻。
为负;在抛出点以上时,一个位移对应两个不同的时刻。
竖直上抛运动的上升和下降阶段具有对称性:
1、速度对称:上升和下降过程经过同一位置时速度等大反向。
2、时间对称:上升和下降过程经过同一段高度的上升时间和下降时间相等。
(二)如何用运动的合成和分解的方法来研究斜抛运动轨迹
斜抛运动的分解与平抛运动的分解方法类似,一般将它分解为水平方向上的匀速直线运动,竖直方向上的竖直上抛运动。根据这个分解方法可以解决很多关于斜抛运动的问题,使得复杂的问题简化为熟悉的直线运动。
建立一个直角坐标系,将坐标系的原点选择在物体的抛出点处,物体运动的轨迹如图所示,将运动看成一个水平方向沿x轴正方向运动,一个竖直方向沿y轴的正方向运动。物体抛出的初速度与x轴正方向之间的夹角为抛射角,用θ表示,在这个坐标系中物体被抛出的初速度![]() 可以沿水平方向分解为
可以沿水平方向分解为![]() ,沿竖直方向分解为
,沿竖直方向分解为![]() ,物体在水平方向没有受到任何外力的作用,做匀速直线运动;在竖直方向上只受到竖直向下的重力作用,做竖直上抛运动,根据匀速直线运动和竖直上抛运动的规律求出任何一时刻的位置x和y,即可得在上述坐标系中确定对应该时刻的一个点,用平滑曲线将这些点连接起来,就可得到斜抛运动物体的抛物线轨迹。
,物体在水平方向没有受到任何外力的作用,做匀速直线运动;在竖直方向上只受到竖直向下的重力作用,做竖直上抛运动,根据匀速直线运动和竖直上抛运动的规律求出任何一时刻的位置x和y,即可得在上述坐标系中确定对应该时刻的一个点,用平滑曲线将这些点连接起来,就可得到斜抛运动物体的抛物线轨迹。
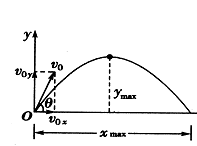
(三)斜抛运动的物体的射高和射程
斜抛运动还可以看成沿初速度的方向和竖直方向的两个运动的合成,竖直方向没有初速度,只受重力作用,做自由落体运动。沿初速度方向没有受到外力作用,做匀速直线运动,速度为![]() 。
。
在实际生活中经常涉及到斜抛运动,特别是体育运动,在研究斜抛运动中,人们最关心射程和射高。像跳高运动员关心的是越过的高度、投掷运动员注重的是水平距离、投篮球和炮弹的运动跟射程和射高都有关系,掌握它能更好地把握生活中的一些现象,有利于解决生活中的一些问题,增长自己各方面的知识。
射高只与竖直方向的分初速度有关,分初速度越大,射得也就越高。抛出点和落地点在同一水平面上时,在空中飞行的时间只与竖直方向的分初速度有关,分初速度越大,空中飞行时间越长。射程跟竖直分速度和水平分速度都有关。以相同速度、不同大小的抛射角抛出的小球做斜抛运动,当抛射角互余即![]() +
+![]() =90°时,水平射程相同;在
=90°时,水平射程相同;在![]() =45°有最大的水平射程。
=45°有最大的水平射程。
将斜抛运动进行分解,如图所示,由图可以看出斜向上抛出的小球,如果抛出点和落地点在同一水平面上,小球有一个最大高度![]() 和最远距离
和最远距离![]() 。物体从抛出点到落地点的水平距离称为射程
。物体从抛出点到落地点的水平距离称为射程![]() =
=![]() ,物体能到达的最大高度称为射高
,物体能到达的最大高度称为射高![]() =
=![]() ,物体从抛出点到落地点的时间称为飞行时间
,物体从抛出点到落地点的时间称为飞行时间![]() 。将初速度分解为水平方向
。将初速度分解为水平方向![]() ,竖直方向
,竖直方向![]() 。从竖直方向看:
。从竖直方向看:![]() ,可以得到射高
,可以得到射高![]() ,物体上升和下降的运动过程对称,时间相同(为飞行时间的一半),
,物体上升和下降的运动过程对称,时间相同(为飞行时间的一半),![]() ,可以得到飞行时间
,可以得到飞行时间![]() ,从水平方向看:
,从水平方向看:![]()
![]()
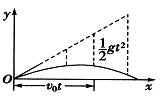
物体做斜抛运动时,如果落地点和抛出点在同一水平面上时,末速度和初速度大小相等,末速度与水平面的夹角和初速度与水平面的夹角相同。
【典型例题】
例1、下列关于斜抛运动的说法中,正确的是
A. 斜抛运动是非匀变速运动
B. 飞行时间只与抛出的初速度有关,水平位移只与初速度和水平方向的夹角有关
C. 落地前在任意几段相等时间内速度的变化量都相同
D. 做斜抛运动的物体落地时的速度一定是竖直向下的
解析:做斜抛运动的物体,仅受重力作用,加速度g恒定,是匀变速曲线运动,A项错误。斜抛运动水平方向为匀速直线运动,故水平速度不变,竖直方向为竖直上抛运动,加速度为g(恒定),故速度在相等时间内变化相等,即合运动在相等时间内速度变化量相同,C项正确。由于水平方向速度恒定,故落地的合速度不可能竖直向下,D项错误。由飞行时间和水平位移的表达式可知,二者都与抛出速度的大小、方向有关,故B项错误。
答案:C
例2、以相同的初速率、不同的抛射角同时抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法正确的是
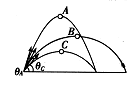
A. A、B、C三球在运动过程中,加速度都相同
B. B球的射程最远,所以最迟落地
C. A球的射高最大,所以最迟落地
D. A、C两球的射程相等,两球的抛射角互为余角,即![]()
解析:A、B、C三球在运动过程中,只受到重力作用,故具有相同的加速度g,A选项正确。斜抛运动可以分成上升和下落两个过程,下落过程就是平抛运动,根据平抛物体在空中的时间只决定于抛出点的高度可知,A球从抛物线顶点落至地面所需的时间最长,再由对称性可知,斜抛物体上升和下落所需的时间是相等的,所以A球最迟落地. 故C选项正确,B选项错误。已知A、C两球的射程相等,根据射程公式![]() 可知
可知![]() ,在
,在![]() ≠
≠![]() 的情况下,必有
的情况下,必有![]() +
+![]() =
=![]() ,才能使等式成立,故D选项正确。
,才能使等式成立,故D选项正确。
答案:ACD
例3、在塔顶上分别以跟水平线成45°角斜向上的、水平的、跟水平线成45°角斜向下的三个方向开枪,子弹射到地面时的速度大小分别为![]() 、
、![]() 和
和![]() (设三个方向射出的子弹的初速度的大小都一样,不计空气阻力),那么
(设三个方向射出的子弹的初速度的大小都一样,不计空气阻力),那么
A. ![]() =
=![]() >
>![]() B.
B. ![]() >
>![]() >
>![]() C.
C. ![]() >
>![]() >
>![]() D.
D. ![]() =
=![]() =
=![]()
解析:设子弹初速度为![]() ,塔高为
,塔高为![]() .三颗子弹落地速度的水平分量分别为
.三颗子弹落地速度的水平分量分别为![]() ,
,![]() ,
,![]() 。三颗子弹落地速度的竖直分量分别为:
。三颗子弹落地速度的竖直分量分别为:
![]()
![]()
![]()
![]()
![]()
![]()
答案:D
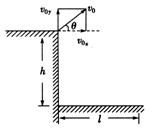
例4、如图所示,从距离墙壁为![]() 的水平地面上的A点,以初速度
的水平地面上的A点,以初速度![]() 、抛射角
、抛射角![]() = 45°,斜向上抛一球,球恰在上升到最高点时与墙相碰,被水平反弹回来,落到地面上的C点,且OC=
= 45°,斜向上抛一球,球恰在上升到最高点时与墙相碰,被水平反弹回来,落到地面上的C点,且OC=![]() /2. 则小球被墙反弹的速度
/2. 则小球被墙反弹的速度![]() 的大小与初速度
的大小与初速度![]() 的大小之比为:
的大小之比为:
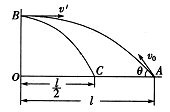
A. 1:2
B. ![]() :1
C.
:1
C. ![]() :1
D.
:1
D. ![]() :1
:1
解析:斜抛运动以其顶点为界,可以分成上升和下降两个过程,这两个过程有一定的对称性。下降过程实际上就是以水平分速度![]() 为初速度的平抛运动。如果小球上升到最高点与墙壁碰撞后速度大小不变,仍为
为初速度的平抛运动。如果小球上升到最高点与墙壁碰撞后速度大小不变,仍为![]() ,则小球碰撞后做平抛运动,轨迹形状与上升时相同,即从B到A,再把B到A的过程与B到C的过程相比较。它们从同一高度被水平抛出,因此,在空中飞行的时间
,则小球碰撞后做平抛运动,轨迹形状与上升时相同,即从B到A,再把B到A的过程与B到C的过程相比较。它们从同一高度被水平抛出,因此,在空中飞行的时间![]() 相等,根据水平位移之比
相等,根据水平位移之比![]() ,可得反弹速度
,可得反弹速度 ![]() ,即
,即![]()
答案:D
四、小结
运动的合成和分解是解决复杂运动的基本方法,分解时所有的矢量都要分解,再看各方向上的速度、受力如何,再根据具体情况分方向解决,各方向计算时注意独立性、等时性和等效性。
【模拟试题】(答题时间:40分钟)
1. 在下列哪种运动中,物体在任意时间内的平均加速度就是物体在任意时刻的即时加速度
A. 匀速直线运动 B.
匀速圆周运动 C.
自由落体运动 D.
斜抛运动
2. 做斜上抛运动的物体
A. 水平分速度不变
B.
加速度不变
C. 在相同的高度处有相同的速度 D.
经过最高点时,即时速度为零
3. 做斜上抛运动的物体,在2 s末经过最高点时的即时速度是15 m/s,g取10m/s2,则初速度,抛射角各为多大?
*4. 已知炮弹的初速度是300 m/s,今把大炮置于高度为800m的山上,要使炮弹命中水平距离是9.6km的地面目标。
求:(1)发射时炮筒的仰角?
(2)炮弹落地时的速度(g取10 m/s2)
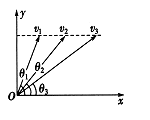
*5. 有一支步枪,先后以不同的速度![]() 、
、![]() 、
、![]() 射出三颗子弹,各速度矢量如图所示,问哪颗子弹的射高最大,哪颗子弹的射程最远,为什么?
射出三颗子弹,各速度矢量如图所示,问哪颗子弹的射高最大,哪颗子弹的射程最远,为什么?
6. 一个人站在地面上用枪瞄准树上的猴子,当子弹从枪口射出时,猴子同时从树上竖直下落(初速度为零),问猴子能否避开子弹的射击?
*7. 斜上抛物体到达最高点时速度为![]() =24 m/s,落地时速度为
=24 m/s,落地时速度为![]() =30 m/s 。如图所示,试求:(1)物体抛出时的速度的大小和方向;(2)物体在空中的飞行时间;(3)射高和水平射程。(g取10 m/s2)
=30 m/s 。如图所示,试求:(1)物体抛出时的速度的大小和方向;(2)物体在空中的飞行时间;(3)射高和水平射程。(g取10 m/s2)
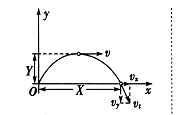
**8. 在![]() =5 m高的平台上,沿着与水平线成
=5 m高的平台上,沿着与水平线成![]() =45°角的方向以初速度
=45°角的方向以初速度![]() 向斜上方抛出一个小球。小球着地点与抛出点之间的水平距离用
向斜上方抛出一个小球。小球着地点与抛出点之间的水平距离用![]() 来表示,如图所示,如果要限制
来表示,如图所示,如果要限制![]() 在0到5 m的范围内,则对
在0到5 m的范围内,则对![]() 的取值有何限制?空气阻力不计,重力加速度g取10 m/s2 。
的取值有何限制?空气阻力不计,重力加速度g取10 m/s2 。
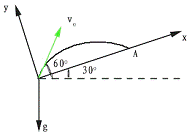
**9. 我方用迫击炮轰击敌人,发射点在山脚,炮弹的发射角为60°,发射速度为150 m/s,炮弹击中倾角为30°的山坡上的敌方目标,如图所示。求炮弹着点A到发射点0的距离?
【试题答案】
1. 答案:ACD
解析:匀速直线运动加速度始终为零;自由落体运动和斜抛运动都是匀变速曲线运动,加速度始终为g
2. 答案:AB
解析:斜抛运动是一个匀变速曲线运动,加速度不变,水平方向是匀速直线运动。
3. 答案:25m/s 53°
解析:上升时间![]() ,即2=
,即2=![]() ,
,![]() ;最高点时只有水平速度,而
;最高点时只有水平速度,而![]() ,即
,即![]() ,两式联立可得
,两式联立可得![]() 25m/s
25m/s ![]() 53°
53°
4. 答案:(1)37°或(48.36°)(2)325m/s
解析:竖直方向为竖直上抛运动![]() ,落点在抛出点下方,所以位移为负
,落点在抛出点下方,所以位移为负
即:![]()
![]()
水平方向为匀速直线运动有:![]()
可解出t和θ
再根据![]()
![]()
![]() 可得结果
可得结果
5. 答案:三颗子弹射高相同,第三颗子弹射程最远
解析:![]()
![]() ,由图可知H和t都相同
,由图可知H和t都相同
![]()
6. 答案:能
解析:子弹在竖直方向上要向上做减速运动,速度减为零后才向下做自由落体运动,而猴子一直做自由落体运动。
7. 答案:(1)30m/s ![]() (2)3.6 s (3)16.2m 86.4m
(2)3.6 s (3)16.2m 86.4m
解析:(1)因为落点和起点在同一水平面,所以![]()
最高点的速度为初速度的水平分量即![]()
![]()
![]()
(2)![]()
(3)![]()
![]()
8. 答案:0≤![]() ≤5m/s
≤5m/s
解析:在空中运动时间![]()
![]()
水平方向位移![]() ≤5
≤5
9. 答案:1500m
解析:把速度和加速度都分解到沿山坡和垂直于山坡两个方向,于是炮弹在垂直于山坡方向做初速度为![]() ,加速度为
,加速度为![]() 的匀变速运动,而沿山坡方向做初速度为
的匀变速运动,而沿山坡方向做初速度为![]() ,加速度为
,加速度为![]() 的匀变速运动,炮弹在垂直于山坡方向位移为零,于是运动时间可由
的匀变速运动,炮弹在垂直于山坡方向位移为零,于是运动时间可由
![]() 来求,
来求,
![]()
![]()
沿山坡方向:
![]()