![]()
课程解读
一、学习目标:
1. 认识圆柱,了解圆柱各部分的名称,掌握圆柱的特征。
2. 理解圆柱的侧面展开图与圆柱各部分的关系。
3. 会用圆柱的体积公式计算圆柱形物体的体积和容积,并能运用公式解决一些简单的问题。
二、重点、难点:
1. 重点:理解并掌握圆柱的特征,认识圆柱侧面的特征。
2. 难点:圆柱体积计算公式的应用。
三、考点分析:
圆柱是生活中常见的几何形体,学习这部分内容有利于发展同学们的空间观念,为进一步应用几何知识解决问题打下基础。本节课的内容要求同学们熟练掌握。这部分内容在考试中经常出现的题型有填空题和解决问题,所占的分值大约为5~8分。
知识梳理
知识点一:圆柱的认识


2. 圆柱的组成:圆柱是由两个底面和一个侧面组成的。
3. 圆柱的特征:
(1)底面的特征:圆柱的上下底面都是圆,并且大小一样。
(2)侧面的特征:圆柱的侧面是曲面。
(3)高的特征:一个圆柱有无数条高。
4. 圆柱的侧面、底面及其之间的关系
圆柱的侧面沿着一条高展开后是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高。
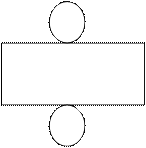
知识点二:圆柱的表面积
1. 圆柱的侧面积=长方形的面积

2. 圆柱体的表面积
圆柱体的表面积指它的侧面积与两个底面积的和
知识点三:圆柱的体积
1. 圆柱体积的意义
一个圆柱所占空间的大小,叫做这个圆柱的体积。
2. 圆柱体积的计算公式V=Sh
典型例题
一、方法应用题
![]()
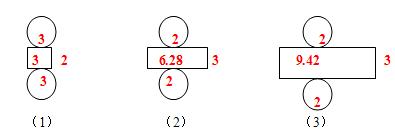
思路分析:
1)题意分析:本题主要考查同学们对于圆柱特征的理解。
2)解题思路:将圆柱的侧面沿着高展开后,得到的是长方形,则长方形的长应该是圆柱的底面周长,显然,图(1)不是,因为长方形的长与圆的直径相等,所以不可能围成圆柱;图(2)中,圆的周长是3.14×2=6.28,与长方形的长相等,所以可以围成圆柱;图(3)中圆的周长是3.14×2=6.28,而长方形的长是9.42,长方形的长比圆的周长长,所以不能围成圆柱。
解答过程:图(2)是圆柱的展开图。
解题后的思考:判断一个图形是不是圆柱的展开图,关键看长方形的长与底面的周长是否相等。

思路分析:
1)题意分析:本题主要考查同学们对于圆柱侧面的理解。
2)解题思路:圆柱的侧面展开图并不一定是沿着高展开,当沿着高展开时,可得到长方形或正方形,若不是沿着高展开,也可能得到一个平行四边形。
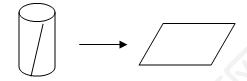
解答过程:选择圆柱的侧面展开图,得不到( C )。
解题后的思考:无论怎样展开,圆柱展开后相对的两条边的长度是相等的,因为圆柱的底面是大小相等的圆,两个底面的周长是相等的,则展开后,这两条边的长度也是相等的,而梯形的上底与下底不相等,因此得不到梯形。

思路分析:
1)题意分析:本题主要考查同学们运用所学知识解决问题的能力。
2)解题思路:此题有两种情况。长方形的任何一条边都可能是原来圆柱的高。当长方形的长是圆柱的高时,则宽就是圆柱的底面周长。当宽是圆柱的高,则长就是圆柱的底面周长,知道底面周长就可以求出底面半径。
解答过程:
(1)当以长
r=C÷2π=12.56÷(2×3.14)=2(cm)
(2)当以宽
r=C÷2π=18.84÷(2×3.14)=3(cm)
答:这个圆柱的底面半径可能是
解题后的思考:同学们在做题时一定要考虑周全,这道题就有两种可能性。所以在做题的时候这两种可能性都要解答出来。

思路分析:
1)题意分析:本题主要考查同学们对于圆柱侧面积知识的应用情况。
2)解题思路:要求前轮转动一周压路的面积实际上就是求底面直径是
解答过程:
S侧=πd·h
=3.14×1.2×1.5
=5.652(平方米)
答:前轮转动一周,压路的面积是5.652平方米。
解题后的思考:圆柱的侧面积等于底面周长乘高,即如果知道底面的一个条件和高,就可以用公式求出圆柱的侧面积。像上面这道题,求压路机前轮转动一周压路的面积,实质上就是求前轮滚筒的侧面积。
二、综合运用题

思路分析:
1)题意分析:本题主要考查同学们对于圆柱体表面的理解以及灵活运用情况。
2)解题思路:圆柱体的高减少
解答过程:
C=18.84÷3=6.28(cm)
S表=C·h+2π·(![]() )²
)²
=6.28×24+2×3.14×(![]() )²
)²
=157(平方厘米)
答:原来这个圆柱体的表面积是157平方厘米。
解题后的思考:圆柱的底面不变,高增加(或减少),表面积也随着增加(或减少),增加(或减少)的面积可以通过其侧面积来分析。


思路分析:
1)题意分析:本题考查同学们对于组合图形的表面积的掌握情况。
2)解题思路:从图中我们可以看出,每个上层圆柱的下底都覆盖了下层圆柱与上层圆柱的上底同样大小的一部分,也就是说,两个相互接触的圆柱共同减少了两个上层圆柱的底面。因此只需要用底层图形表面积加上上层图形的侧面积即可。
解答过程:
3.14×3²×2+3×2×3.14×1+2×2×3.14×1+1×2×3.14×1
=56.52+2×3.14×(3+2+1)
=56.52+37.68
=94.2(dm²)
答:这个立体图形的表面积是94.2dm²。
解题后的思考:组合图形表面积的计算,只需用底层图形表面积加上上层叠加图形的侧面积即可。
三、思维突破题

思路分析:
1)题意分析:本题主要考查同学们运用所学知识解决生活中的问题的能力。
2)解题思路:
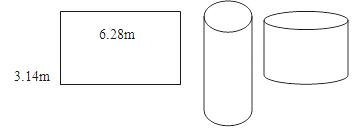
要把一张长方形芦席围成一个圆柱形粮囤,如图,有两种围法,一种以长作圆柱的高,则宽就是底面圆的周长,另一种是以宽作为圆柱的高,长就是底面圆的周长。通过计算比较就可以知道哪种围法的容积大了。
解答过程:

解题后的思考:把一个长方形围成一个圆柱,把宽作为圆柱的高,长作为圆柱的底面周长,这种围法的容积要大一些。
提分技巧
本节课主要讲解的就是圆柱的认识,加强了与现实生活中的联系,并且加强了对图形特征的探索,同学们通过观察探索培养了自主解决问题的能力。同学们要牢牢掌握圆柱的表面积和体积公式,并做到能够灵活运用。
预习导学
下节课我们将一起来复习有关圆锥的知识。
一、预习新知
圆锥有什么特征?
二、预习点拨
探究与反思
探究任务一:圆锥的组成
【反思】圆锥是由哪几部分组成的?
探究任务二:圆锥的体积公式
【反思】圆柱与圆锥之间有什么关系?
同步练习(答题时间:45分钟)
一、填空
1. 圆柱的两个圆面叫做( ),它们是( )的圆形;周围的面叫做( );圆柱两个底面之间的距离叫做( )。一个圆柱有( )条高。
2. 把一张长方形的纸的一条边固定贴在一根木棒上,然后快速转动,得到一个( )。
3. 一个圆柱沿侧面展开后得到一个长方形,长是12.56厘米,宽是3厘米。这个圆柱的底面周长是( )厘米,高是( ) 厘米。
4. 一个圆柱沿侧面展开后得到一个正方形,边长是9.42厘米。这个圆柱的底面周长是( )厘米,高是( ) 厘米。
二、判断
1. 上下两个底面相等的物体一定是圆柱体。
( )
2. 圆柱的侧面沿着高展开后会得到一个长方形或者正方形。 ( )
3. 同一个圆柱底面之间的距离处处相等。
( )
4. 一个圆柱,底面周长是
5. 一个圆柱,底面半径是
三、计算
1. 直接写出得数。
3.14×3=
3.14×4=
3.14×6=
3.14×7=
3.14×10=
3.14×0.5=
3.14×0.8=
3.14×20=
2. 求下面圆柱形的侧面积。
(1)底面直径是
3. 求下面圆柱的表面积。
(1)底面直径是
(2)底面半径是2分米,高是20分米。
四、解决实际问题
1. 一个没有盖的圆柱形铁罐,底面直径是10厘米,高是4厘米,做这个铁罐要用铁皮多少平方厘米?(得数保留整十平方厘米)
2. 一台压路机,前轮直径
(1)这台压路机工作1分钟前进了多少米?
(2)工作1分钟前轮压过的路面是多少平方米?
3. 一个没有盖的圆柱形水桶,底面直径是4分米,高是8分米,要在水桶的里、外面都涂上防锈漆,油漆的面积大约是多少平方分米?(得数保留整数。)
![]()
试题答案
一、填空
1. 圆柱的两个圆面叫做( 底面 ),它们是(大小一样)的圆形;周围的面叫做(侧面 );圆柱两个底面之间的距离叫做( 高 )。一个圆柱有(无数)条高。
2. 把一张长方形的纸的一条边固定贴在一根木棒上,然后快速转动,得到一个( 圆柱
)。
3. 一个圆柱沿侧面展开后得到一个长方形,长是12.56厘米,宽是3厘米。这个圆柱的底面周长是( 12.56 )厘米,高是( 3 ) 厘米。
4. 一个圆柱沿侧面展开后得到一个正方形,边长是9.42厘米。这个圆柱的底面周长是( 9.42 )厘米,高是( 9.42 ) 厘米。
二、判断
1. 上下两个底面相等的物体一定是圆柱体。
( × )
2. 圆柱的侧面沿着高展开后会得到一个长方形或者正方形。 ( √ )
3. 同一个圆柱底面之间的距离处处相等。
( √ )
4. 一个圆柱,底面周长是
5. 一个圆柱,底面半径是
三、计算。
1. 直接写出得数。
3.14×3=9.42 3.14×4=12.56 3.14×6=18.84 3.14×7=21.98
3.14×10=31.4 3.14×0.5=1.57 3.14×0.8=2.512 3.14×20=62.8
2. 求下面圆柱形的侧面积。
(1)底面直径是
0.5×3.14×2=3.14(m²)
2×2×3.14×5=62.8(dm²)
3. 求下面圆柱形的表面积。
底面直径是
圆柱侧面积:3.14×10×16=502.4(cm²)
底面的面积:3.14×(![]() )²×2=157(cm²)
)²×2=157(cm²)
圆柱的表面积:502.4+157=659.4(cm²)
答:圆柱的表面积为659.4平方厘米。
四、解决实际问题。
1. 一个没有盖的圆柱形铁罐,底面直径是10厘米,高是4厘米,做这个铁罐要用铁皮多少平方厘米?(得数保留整十平方厘米)
3.14×10×4=125.6(平方厘米)
3.14×(![]() )²=78.5(平方厘米)
)²=78.5(平方厘米)
125.6+78.5=204.1(平方厘米)≈210(平方厘米)
答:做这个铁罐要用铁皮210平方厘米。
2. 一台压路机,前轮直径
(1)这台压路机工作1分钟前进了多少米?
3.14×1×1.2×15=56.52(米)
答:这台压路机工作1分钟前进了
(2)工作1分钟前轮压过的路面是多少平方米?
56.52×1.2=67.824(平方米)
答:工作1分钟前轮压过的路面是67.824平方米。
3. 一个没有盖的圆柱形水桶,底面直径是4分米,高是8分米,要在水桶的里、外面都涂上防锈漆,油漆的面积大约是多少平方分米?(得数保留整数。)
3.14×4×8×2+3.14×(![]() )²×2=226.08≈226(平方分米)
)²×2=226.08≈226(平方分米)
答:油漆的面积大约是226平方分米。