【本讲教育信息】

一. 教学内容：

解简易方程

二. 重点、难点：

学习重点：

1. 理解方程的意义和有关概念。

2. 会解简易方程。

学习难点：

1. 掌握形如的简易方程的解法。

2. 理解方程的意义及有关的概念。

教学过程：

一、“方程”、“方程的解”、“解方程”的意义

我们已经学习了用字母表示数，今天来学习简易方程。

（一）认识方程

1. 天平是测量物体重量的一种工具，在它的左右两边有两个盘，当在天平的两边放上重量相等的物体时，天平就会保持平衡，即指针指向正中。

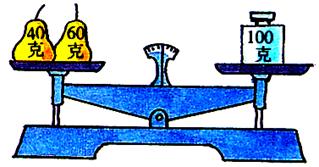
（1）在天平的左边放一个40克、一个60克的梨，右边放一个100克的砝码，天平怎样了？（平衡了，说明天平两边所放物体的重量是相等的。）

用式子表示：

（2）如果在天平的左边放一个40克的梨，右边放一个100克的砝码，天平怎样？说明什么？用一个式子怎样表示？

（天平不平衡，说明天平两边所放物体的重量不相等。

用式子表示：）

（3）

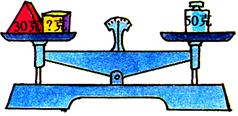
这个天平保持着平衡，说明天平左右两边的重量相等了。

现在我们要求出左盘上的重多少克？

要求的重量，通常叫做未知数，用字母x表示。

用式子表示：

（4）

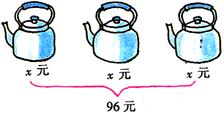
每个电壶的价钱是x元，3个电壶的总价是3x元，也就是96元，用式子表示：。

2. 比较分类：

（1）以上四个式子按左右两边的关系分类，哪几个式子是一类？为什么？

表示不相等关系的式子：

表示相等关系的式子：

所以，表示相等关系的式子叫做等式。

（2）请把以上三个等式分类，哪几个等式是一类？为什么？

一类：等式中不含未知数：

二类：等式中含有未知数：

像第二类中，这样的等式，就是方程。

方程必须满足几个条件？什么叫方程？

（方程必须满足两个条件：（1）必须是等式；（2）必须含有未知数。）

含有未知数的等式，叫做方程。

（3）判断：

①下面哪些是方程，哪些不是方程，为什么？

②所有的等式都是方程。（ ）

③所有的方程都是等式。（ ）

思考：等式与方程有什么关系？

等式中包含有方程，方程是特殊的等式，图式：

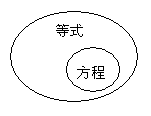
（二）“方程的解”和“解方程”的意义

1. 理解“方程的解”：

观察天平，当x是多少克时，可以使方程左右两边相等？

观察电饭锅图：当x等于多少元时，使这个方程左右两边相等？

小结：像20、210这些数叫做未知数的值，它们分别是能使以上二个方程左右两边相等的未知数的值，分别叫这些方程的解。

什么叫方程的解？

（使方程左右两边相等的未知数的值，叫做方程的解。）

2. 理解“解方程”：

方程的解是20，你是怎么知道的？

根据：一个加数＝和－另一个加数

我们计算出的这个过程，实际上就是解方程。

什么是解方程？（求方程的解的过程叫做解方程。）

以前，我们做过一些求未知数x的题目，实际上就是解方程。

例1. 解方程

解：（根据什么？）

检验：把代入原方程，

左边：，和右边相等。

是原方程的解。

注意：解题格式：等号对齐；解方程要写“解”。以后解方程时，除了要求写出检验以外，都用口算进行检验，养成验算的良好习惯，以保证解题的正确。

3. 区分“方程的解”与“解方程”：

方程的解：指的是一个数，它表示未知数等于多少时，能使方程左右两边相等。

解方程：指求出这个数的过程。

二、解方程：

例2. 列出方程，并求出方程的解。

一个数的2.4倍是12，求这个数。

解：设这个数是x

（口算检验）

注意：如果题目中的未知数没用字母表示，解题时要先把未知数设为x。

练习：

（1）7.2加上x等于10.8

（2）一个数除以1.6等于8

例3. 看图列方程，并求出方程的解。

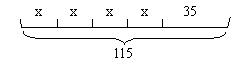
解： 这是几步运算？

把4x看作一个数

检验：把代入原方程。

左边： ，和右边 。

原方程的解 。

小结：解二步运算的方程关键是把含有x的部分看作一个数，并求出它的值，再求出x的值。

例4. 一个数的4倍减去18与4.5的积，差是56，求这个数。

解：设这个数是x

这是几步运算？（三步）

首先按运算顺序解，先算出的积

最后按二步运算题解。

（口算检验）

小结：在含有三步运算的方程中，按照运算顺序可以计算的部分要先计算出来，使方程化简为二步运算。

例5. 解方程：

这个方程与学过的方程有什么不同？

解： （有两部分含有x）

检验：把代入原方程

左边：____________________________________

和右边_______________

________原方程的解。

例6. 解方程

解：

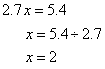
【模拟试题】（答题时间：30分钟）

1. 在下面的式子中，是方程的在括号里打“√”，不是的打“×”。

（1）（ ） （2）44+60=110（ ）

（3）405÷x=81（ ） （4）10x>201（ ）

（5）x－123（ ） （6）1.7x=0（ ）

（7）1.7x+3.8（ ） （8）（ ）

2. 在括号里找出方程的解，并在下面画上横线

（1） （x=16，x=6）

（2） （x=24，x=8）

（3） （x=1.6，x=16）

3. 用直线把下面各个方程与它的解连接起来

x=18

x=10.2

x=0.5

x=0.08

x=20.7

x=11.4

4. 判断

（1）含有未知数的式子叫做方程。（ ）

（2）“解方程”和“方程的解”意义相同。（ ）

（3）8x=0，x的值表示没有，所以8x=0没有解。（ ）

（4）方程是等式，等式不一定是方程。（ ）

（5）的解是5.8。（ ）

5.解下列方程：（1）、（2）题写出检验过程

（1） （2）

（3） （4）

6. 列方程，并求出方程的解。

（1）一个数加上它的2倍后，和是12.3，求这个数。

（3）一个数乘8的6倍与这个数加上14.1的和相等，求这个数。

*在下面的□里填数，使等式成立

（1）1990+（25×□-50）÷6=2003

（2）0.25×(4.85×□+6.15×□-□)=9（□里填同一个数）

【试题答案】

1. 在下面的式子中，是方程的在括号里打“√”，不是的打“×”。

（1）（√） （2）44+60=110（×）

（3）405÷x=81（√） （4）10x>201（×）

（5）x－123（×） （6）1.7x=0（√）

（7）1.7x+3.8（×） （8）（×）

2. 在括号里找出方程的解，并在下面画上横线

（1） （x=16，x=6）

（2） （x=24，x=8）

（3） （x=1.6，x=16）

3. 用直线把下面各个方程与它的解连接起来

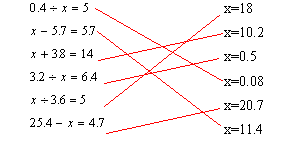
4. 判断

（1）含有未知数的式子叫做方程。（×）

（2）“解方程”和“方程的解”意义相同。（×）

（3）8x=0，x的值表示没有，所以8x=0没有解。（×）

（4）方程是等式，等式不一定是方程。（√）

（5）的解是5.8。（×）

5.解下列方程：（1）、（2）题写出检验过程

（1） （2）

解： 解：

x=27

检验：把x=0.34代入原方程 检验：把x=27代入原方程

（3） （4）

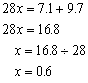
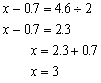
6. 列方程，并求出方程的解。

（1）一个数加上它的2倍后，和是12.3，求这个数。

解：设这个数是x

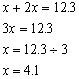
（3）一个数乘8的6倍与这个数加上14.1的和相等，求这个数。

解：设这个数是x

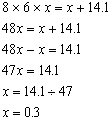
*在下面的□里填数，使等式成立

（1）1990+（25×□-50）÷6=2003

□=5.12

（2）0.25×(4.85×□+6.15×□-□)=9（□里填同一个数）

□=3.6