【本讲教育信息】
一. 教学内容：
第二十四章 圆（下）
第4节 正多边形和圆
二. 教学目标：
1. 掌握正多边形的定义、性质及相关的概念。
2. 会进行正多边形的有关计算。
三. 教学重点、难点：
1. 重点：正多边形性质、相关概念及有关计算。
2. 难点：正多边形有关计算。
四. 教学过程：
（一）知识点：
1. 正多边形：各边相等，各角也相等的多边形叫正多边形。
2. 正多边形与圆的关系：
把圆分成
等份，依次联结各分点，所得的多边形是这个圆的内接正n边形。
3. 正多边形的性质：
（1）任何一个正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆。
（2）正多边形都是轴对称图形，一个正n边形有n条对称轴，每条对称轴都通过正n边形的中心。
（3）边数为偶数的正多边形是中心对称图形，它的中心就是对称中心。
4. 与正多边形有关的概念
正多边形的中心：正多边形外接圆（或内切圆）的圆心。
正多边形的半径：正多边形外接圆的半径。
正多边形的边心距：正多边形内切圆的半径。
正多边形的中心角：正多边形每一边所对的外接圆的圆心角。
【典型例题】
例1. （1）如果一个正多边形的中心角为24°，那么它的边数是_____________。
（2）正多边形的一个外角等于45°，那么这正多边形的内角和等于__________°，中心角等于_____________°。
解：（1）15 （2）1080，45
例2. 已知：如图所示，正六边形ABCDEF的半径为R，求这个正六边形的边长a6，周长P6和面积S6。
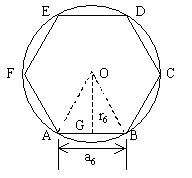
分析：正六边形的半径和边心距将正六边形分成12个全等的直角三角形，抓住其中一个直角三角形便可求出相关量。
解：如图所示，作半径OA、OB，作
得
。
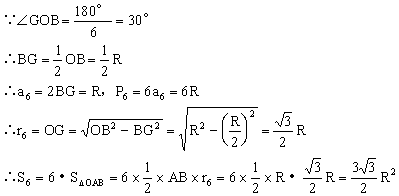
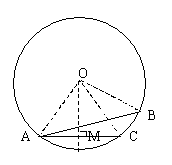
例3. 已知：圆内接正方形的面积是8，求同圆的内接正六边形的面积。
解：如图所示，设正方形边长为AB，正六边形边长为AC，过O作
连结OB、OA、OC
∵正方形面积是8
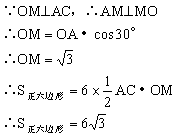
例4. 已知：如图所示，△OAB为正三角形，以O为圆心，OA为半径作圆O，直径FC//AB，AO、BO的延长线交圆O于D、E，求证：六边形ABCDEF是正六边形。
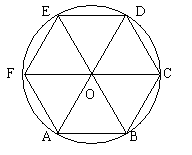
分析：已知A、B、C、D、E、F在圆上，只要证明它们是圆O的六等分点即可。
证明：∵△OAB是正三角形
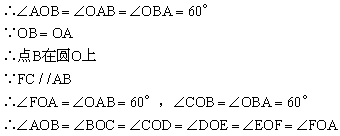
∴六边形ABCDEF是正六边形
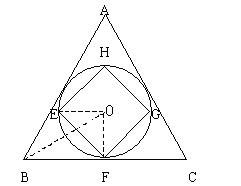
例5. 已知：如图所示，圆O为正三角形ABC的内切圆，EFGH是圆O的内接正方形，且
，求正三角形的周长。
解：连结OB、OE、OF在等腰直角三角形OEF中
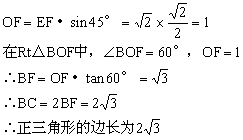
∴正三角形的周长为
（三）本章小结
【模拟试题】（答题时间：30分钟）
一. 填空题
（1）正三角形的半径为R，则边长为_____________，边心距为_____________，面积为_____________，若正三角形边长为a，则这个三角形的半径为_____________，内切圆半径为_____________，这个三角形的高为_____________。
（2）正n边形的一个外角为30°，则它的边数为_____________，它的内角和为_____________，当它的边心距为r时，它的边长为_____________，面积为_____________。
（3）如果一个正n边形的一个外角等于它的一个内角的三分之二，则这个正n边形的边数为_____________。
（4）正六边形的边长为1，则它的半径为_____________，面积为_____________。
（5）同圆的内接三角形、正四边形、正六边形的边长之比为_____________。
（6）如果圆的面积是
那么这个圆的外切正方形的面积是_____________。
二. 解答题
（1）已知：正三角形的边长为a，求它的内切圆与外接圆组成的圆环面积。
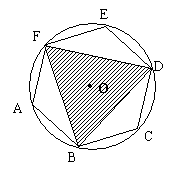
（2）已知：如图所示，正六边形ABCDEF内接于圆O，图中阴影部分面积为
，求圆O的半径。
（3）已知圆O的半径为R，求它的内接正三角形的内切圆的内接正方形的周长。
【试题答案】
一. 填空题
（1）
（2）12，1800°，
（3）5
（4）1，
（5）
（6）12
二. 解答题
（1）
（2）4 （3）