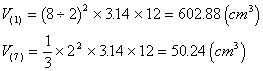【本讲教育信息】
一. 教学内容：
圆柱和圆锥——面的旋转和圆柱体的表面积
二. 重点、难点：
各种图形旋转成的几何体，建立空间思维能力
三. 具体内容：
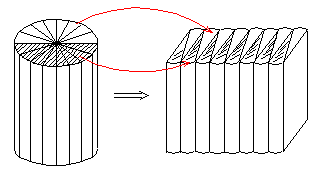
现实生活中的空间几何体
这些图片中的物体具有什么几何结构特征？你能对它们进行分类吗？分类的依据是什么？
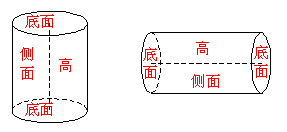
1. 圆柱的结构特征
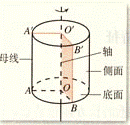
以矩形的一边所在直线为旋转轴，其余三边旋转形成的曲面所围成的几何体叫做圆柱。
圆柱用表示它的轴的字母表示，如上图的圆柱表示为：圆柱：Ｏ'Ｏ
圆柱和棱柱统称为柱体。
2. 圆锥的结构特征
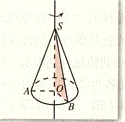
以直角三角形的一边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫做圆锥。圆锥也用表示它的轴的字母表示，上图表示为：圆锥：SO
圆锥与棱锥统称为锥体。
3. 圆台
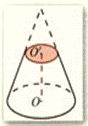
用一个平行于圆锥底面的平面去截圆锥，底面与截面之间的部分，这样的几何体叫做圆台。
与圆柱和圆锥一样，圆台也有轴、底面、侧面、母线，试一试在上图中标出它们，并用字母将上图的圆台表示出来。
棱台与圆台统称为台体。
4. 球
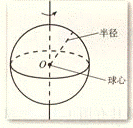
以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的几何体叫做球体。
球常用表示球心的字母Ｏ表示，上图中的球就表示为：球Ｏ
5. 棱柱的结构特征
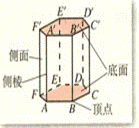
有两个面互相平行；其余各面都是平行四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。
我们用表示底面各顶点的字母表示棱柱。如上图中的棱柱，表示为：棱柱ABCDEF－A'B'C'D'E'F'。
底面是三角形、四边形、五边形……的棱柱分别叫三棱柱、四棱柱、五棱柱……
6. 棱锥的结构特征
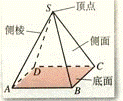
一般地，有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥。
棱锥用表示顶点和底面各顶点的字母表示，上图的四棱锥表示为：棱锥：S-ABCD
分类：
正棱锥：底面是正多边形,并且水平放置.它的顶点又在过正多边形的铅垂线上.
斜棱锥：
7. 棱台
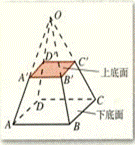
用一个平行于棱锥底面的平面去截棱锥，底面与截面之间的部分，这样的几何体叫做棱台。
与棱柱的表示一样，上图的棱台表示为：棱台：ABCD－A'B'C'D'
分类：
正棱台：由正棱锥截得的棱台
斜棱台：由斜棱锥截得的棱台
观察下列物体，它们表示的几何体不属于前面学习过的任何一种几何体，我们如何描述它们的结构特征呢？
洗洁精瓶子是由两个圆柱和两个圆台组成的，分解有如图。
现实世界中，我们看到的物体大多由具有柱、锥、台、球等几何结构特征的物体组合而成。其他的图片中，你能描述出它们分别是由什么几何体组成的吗？
【典型例题】
例1. 一个没盖的圆柱形铁皮小水桶，高是24厘米，底面直径是20厘米。做这个水桶要用铁皮多少平方厘米？（保留整百数平方厘米）
解答：（1）水桶的底面积？（几个底面积？为什么？）
（ ）（括号内应填什么单位？）
（2）水桶的侧面积：
（ ）（括号内应填什么单位？）
（3）需要的铁皮：
（平方厘米）
答：做这个水桶大约需要用铁皮1900平方厘米。
注意：这里不能用四舍五入法取近似值，因为实际使用的铁皮要比计算的结果多一些。要求保留整百平方厘米，省略的位上即使是4或比4小，都要向前位进1。这种取近似值的方法叫做进一法。
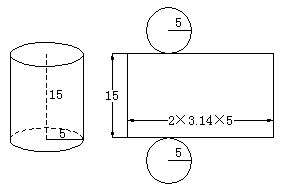
例2. 有一张长方形铁皮，如图剪下阴影部分制成圆柱体（单位：分米），求这个圆柱体的表面积。（提示：圆桶盖的周长等于长方形铁皮的长。）
分析：因为圆桶盖的周长等于长方形铁皮的长，利用这个条件可以求出圆桶盖的直径，还可以求出圆桶的高。
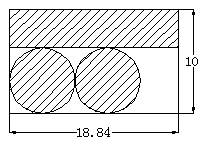
解：圆桶盖的直径 
（dm）
圆桶的高 
（dm）
圆桶的表面积
（dm2）
答：这个圆柱体的表面积是131.88平方分米。
例3. 一个圆柱形油桶，底面直径4分米，高5分米。这个油桶的体积是多少立方分米？
解：（1）底面半径：
（ ）（括号里填什么单位？）
（2）底面积： 
（ ）（括号里填什么单位？）
（3）油桶的体积： 
（ ）（括号里填什么单位？）
答：这个油桶的体积是62.8立方分米。
例4.
如图所示，压路机前轱辘长15米，前轱辘的直径为1.2米，前轱辘转动一周的面积是多少平方米？
解：压路机前轱辘转动一周的面积就是求圆柱体的侧面积。
S＝Ch
C＝1.2 
3.14＝3.768
S＝3.768 15＝56.52
答：前轱辘转动一周的面积是56.52平方米。
例5.
一个圆柱形水池，在池壁和底面都要镶上瓷砖，水池底面直径6米，池深1.2米，镶瓷砖的面积是多少？
解：圆柱形水池只有两个面：一个侧面和一个圆形底面，镶瓷砖的面积就是在求圆柱的侧面和一个底面的面积。
（1）侧面积：S＝Ch＝6
3.14 1.2＝22.608
（2）圆形底面积：r＝6 
2＝3 S＝3.14 3 
＝28.26
（3）镶瓷砖的面积：22.608+28.26＝50.868（m ）
答：镶瓷砖的面积是50.868平方米。
【模拟试题】（答题时间：30分钟）
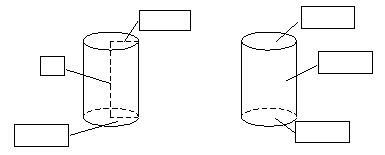
1. 指出下列圆柱的底面、侧面和高。
2. 计算下面圆柱体的表面积。（单位：厘米）
3. 一根圆柱形钢材长4米，横截面的直径是2厘米，每立方厘米重7.8克，这根钢材重多少克？
4. 认一认，填一填。
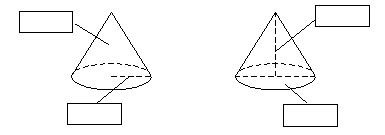
5. 把对应的部分用线连一连。
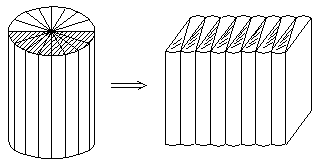
6. 按照图意剪一剪。
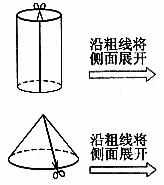
7. 仔细观察，研究圆柱和圆锥的关系。（单位：cm）
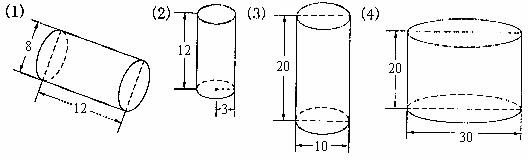
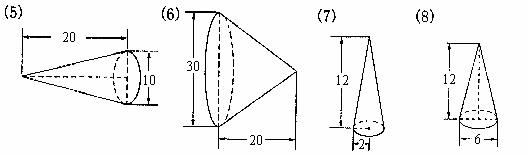
a. 按要求填表。
|
圆柱体 |
与圆柱体等底等高的圆锥体 |
||||||
|
图形序号 |
S |
h |
V |
图形序号 |
S |
h |
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b. 把这些圆柱、圆锥按照体积之间的关系分成两类。（把序号填入圈内）
c. 上面8个图形中还有哪几个图形需要单独计算体积，请算一下。
【试题答案】
1. 指出下列圆柱的底面、侧面和高。
2. 计算下面圆柱体的表面积。（单位：厘米）
解：（1）侧面积： 
（2）底面积： 
（3）表面积： 
答：圆柱体的表面积是628平方厘米。
3. 一根圆柱形钢材长4米，横截面的直径是2厘米，每立方厘米重7.8克，这根钢材重多少克？
解：（1）底面半径： 
（2）圆柱体积： 
（3）钢材的重量： 
答：这根钢材重9796.8克。
4. 认一认，填一填。
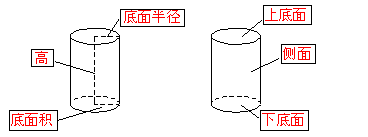
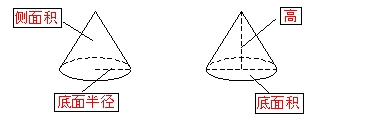
5. 把对应的部分用线连一连。
6. 按照图意剪一剪。
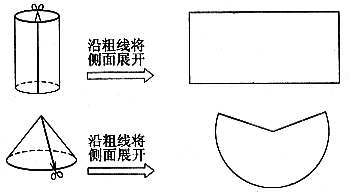
7. 仔细观察，研究圆柱和圆锥的关系。（单位：cm）
a. 按要求填表。
|
圆柱体 |
与圆柱体等底等高的圆锥体 |
||||||
|
图形序号 |
S |
h |
V |
图形序号 |
S |
h |
V |
|
（2） |
28.26 cm2 |
12 cm |
339.12 cm3 |
（8） |
28.26 cm2 |
12 cm |
113.04 cm3 |
|
（4） |
706.5 cm2 |
20 cm |
14130 cm3 |
（6） |
706.5 cm2 |
20 cm |
4710 cm3 |
|
（3） |
78.5 cm2 |
20 cm |
1570 cm3 |
（5） |
78.5 cm2 |
20 cm |
|
b. 把这些圆柱、圆锥按照体积之间的关系分成两类。（把序号填入圈内）
c. 上面8个图形中还有哪几个图形需要单独计算体积，请算一下。
