【本讲教育信息】

一、教学内容：

锐角三角函数

1. 锐角三角函数的定义

2. 锐角三角函数性质

3. 特殊角的三角函数值

4. 解直角三角形及应用

二、知识要点：

锐角三角函数是解决现实世界中测量、建筑、工程技术等问题的重要数学工具。在图形中研究各个元素之间的关系（主要是边角之间的关系），把这种关系用数量的形式表示出来，就是数形结合的思想方法。学生需要理解角的三角函数（正弦、余弦、正切）的概念以及熟悉特殊角的三角函数值等知识，能够联系实际，构建数学模型，利用解直角三角形的知识解决问题。

1. 锐角三角函数的定义：

锐角三角函数概念是学习解直角三角形的基础，在解决边之比在不同三角形中的灵活转化的问题时，不必写繁琐的相似过程，方法更加简洁；同时与高中三角函数的知识相衔接。初步了解正弦、余弦、正切的概念；能较正确地用sinA、cosA、tanA表示直角三角形中两边的比；

归纳三角函数定义。

sinA=，cosA=，tanA=

例：如图所示的Rt△ABC中，∠ACB=90°，BC=4，CA=3，分别求sinA，cosA，tanA的值。

分析：锐角三角函数基本概念的应用

解：由勾股定理AB===5

sinA=，cosA=，tanA=

点评：熟练掌握锐角三角函数中边的对应关系.

2. 锐角三角函数性质：

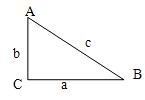
我们在了解三角函数概念的同时，三角函数性质也是方便解题的重要手段. 主要包括同角三角函数性质和互为余角三角函数性质.

⑴同角三角函数满足：

⑵互为余角三角函数满足：sinA=cosB，cosA=sinB，tanA·tanB=1（A+B=90°）

如图：，，，，，，可以推导出上述公式.

例：若sinα– cosα=，求sinα·cosα的值.

分析：若题中出现sinα±cosα的表达式，我们都可以把含sinα±cosα的等式两边平方；

解：（sinα– cosα）=（），∴sinα－2 sinαcosα+ cosα=，

∵sin²α+ cos²α=1，∴sinα·cosα=

点评：充分利用sinα+ cosα=1是解题的关键.

思考题：求tan41°·tan42°·……·tan48°·tan49°的值.

3. 特殊角的三角函数值：

在引入正弦、余弦的概念后，相应的求出30°、45°、60°角的正弦、余弦值。在求值时，要充分利用下面两个图形，建立起数与形之间的联系。并用数形结合的方法记忆。

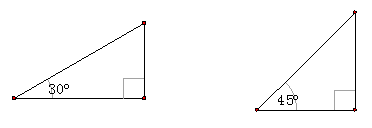
我们知道，30°角的RT△中，三边的关系为1：2：；45°角的RT△中，三边的关系为1：1：，如此，根据锐角三角函数的概念，不难记住特殊角的三角函数值.

例：cos30°－

分析：特殊角的三角函数值问题，分别代入相应的函数值；

解：原式====

点评：根式内存在根式的时候，多考虑用完全平方公式去根号，更方便解题.

4. 解直角三角形及应用：

了解到在含30º角、45º角的直角三角形中，相应的边与角之间有确定的对应关系，那么对于一般的直角三角形，边与角之间是否也有确定的对应关系呢？

在直角三角形ABC中，∠C=90°，a、b、c、∠A、∠B这五个元素间有哪些等量关系呢？

（1）边角之间关系：sinA= cosA= tanA=

（2）三边之间关系：a² +b² =c² （勾股定理）

（3）锐角之间关系：∠A+∠B=90°.

以上三点正是解直角三角形的依据.

例1：如图，东西两炮台A、B相距2000米，同时发现入侵敌舰C，炮台A测得敌舰C在它的南偏东40°的方向，炮台B测得敌舰C在它的正南方，试求敌舰与两炮台的距离。

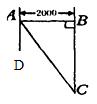
分析：本题中，已知条件是什么？（AB＝2000米，∠CAB＝90°－∠CAD＝50°），那么求AC的长是用“弦”还是用“切”呢？求BC的长呢？显然，AC是直角三角形的斜边，应该用余弦函数，而求BC的长可以用正切函数，也可以用余切函数。

解：cos∠CAB=，∴AC==；

tan∠CAB=，∴°=；

请同学们思考以下问题：

（1）在AC求出后，能否用勾股定理求得BC；

（2）在这道题中，是否可用正弦函数求AC，是否可以用余切函数求得BC。

点评：通过这道例题的分析和挖掘，可以明确在求解直角三角形时可以根据题目的具体条件选择不同的“工具”以达到目的。

例2：如图，厂房屋顶人字架（等腰三角形）的跨度为10米，∠A=26°，求中柱BC（C为底边中点）和上弦AB的长（精确到0. 01米）.

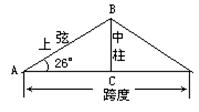
分析：同学们对照图形，根据题意，思考题目中的每句话对应图中的哪个角或边，本题已知什么，求什么？由题意知，△ABC为直角三角形，∠ACB=90°，∠A=26°，AC=5米，可利用解Rt△ABC的方法求出BC和AB. 把实际问题转化为数学问题后，同学们可自行完成

点评：求出中柱BC的长为2.44米后，我们也可以利用正弦计算上弦AB的长。

不仅掌握选何种关系式，更重要的是知道为什么选这个关系式，以培养分析问题、解决问题的能力及计算能力，形成良好的学习习惯. 另外，本题是把解等腰三角形的问题转化为解直角三角形的问题，渗透了转化的数学思想.

三、重点难点：

1、重点：计算特殊角的三角函数值及有关三角函数的代数式的值是本章的重点内容。

2、难点：解直角三角形或构造直角三角形解特殊的斜三角形；建立三角函数模型解决测量、航海和工程等方面的实际问题，这是本章教学的难点。

【典型例题】

例题1、在Rt△ABC中，∠C=90°，BC=5，且sinB=，试分别求AC、AB的值.

【分析】利用锐角三角函数值并借助勾股定理是解这类题的常用方法.

解：∵ 在Rt△ABC中，∠C=90°，

故设AC=2x，则AB=3x.

由勾股定理得AB²－AC²=BC²，

即9x²－4x²=25， ∴ x=.

∴ AC=2x=2，AB=3x=3.

【点评】 解这道题的关键是：根据正弦函数的定义，把握准图形的特征，确定出∠B的对边、斜边、邻边. 同时直角三角形的勾股定理为计算提供的有利保障是不可忽视的.

例题2、如图，在△ABC中，D是AB的中点，CD⊥AC于C，且tan∠BCD=，求sinA，cosA，tanA的值.

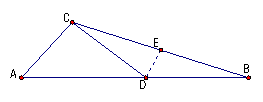
【分析】 解答本题的突破口是将∠BCD转化为直角三角形中的角.

解：过点D作DE⊥CD于D，交BC于点E，

在Rt△CDE中，∵ tan∠BCD=，设DE=x，则CD=3x.

又∵ CD⊥AC，∴ DE∥AC.

又∵ D为AB的中点，∴ E为BC的中点，∴ DE=AC， ∴ AC=2DE=2x.

在Rt△ACD中∠ACD=90°，AC=2x，CD=3x，

∴；

∴；

【点评】在题设中出现的tan∠BCD=， 由于∠BCD所在的三角形并非是直角三角形，因而给解题带来一些困难，此时如果联想起正切函数的定义，想方设法构造出一个与之相关的直角三角形就顺理成章了，另外三角形的中位线的判定及其性质在本例中得到了充分利用，为计算∠A的正弦值，余弦值，正切值架起了桥梁，要善于从中总结经验.

例题3、如果0°<α<90°，且||+，求tanα的值.

【分析】 两个非负数和为零，则这两个数同时为零，便可求得sinα和cosα的值.

解：∵||≥0，≥0，

且||+，

∴=0，=0.

∴ ，（舍去），.

∵ 在0°<α<90°中，

∴ α=30°.

∴ tanα=tan30°=.

【点评】本题的突破口是两个非负数和为零的条件是“这两个数同时为零”，从而求出sinα和cosα的值，由特殊值求出特殊角，另外本题也可以不求出α的度数，直接利用同角的三角函数间的关系求tanα的值.

例题4、已知等腰三角形一腰上的高为1，且这条高与底的夹角的正弦值为，求该三角形的面积.

【分析】 已知高，再求出底边，便可求出面积的值.

解：根据题意画出图形，如下：

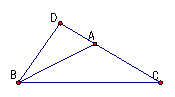
∵ 高BD与底边BC的夹角的正弦值为，

∴ 在Rt△BCD中， sin∠CBD=

∴ ∠CBD=60° . ∴ ∠C=30°.

在△ABC中，AB=AC ，∴ ∠ABC=∠C=30°.

∴ ∠ABD=∠CBD－∠CBA =60°－30°=30°.

在Rt△ABD中，，

∴ S_△ABC=AC·BD

【点评】本例中等腰三角形腰上的高在三角形的外部，否则不能满足高与底的夹角为60°.

例题5、如图，某海防哨所（o）发现在它的北偏西30°距离500m的A处有一艘船。该船向正东方向航行，经过3分钟到达哨所东北方向的B处。求这艘船的航速是每时多少km？（取1.7）

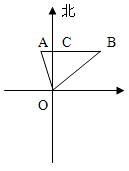
【分析】 1、AB与正北方向有什么位置关系？

2、欲求速度，题中已知时间，还需什么条件？

3、如何得到

解：设AB与正北方向交于点C，则OC⊥AB。

在Rt△AOC中，OA=500m，∠AOC=30°，

∴ AC=OA sin∠AOC=500sin30°=500×=250（m）.

OC=OAcos∠AOC=500cos30°=500×=250（m）.

在Rt△COB中，∠BOC=45°，

∴BC=OC=250（m）

∴AB=AC+BC=250+250=250（1+）≈250（1+1.7）=675（m）.

船速为675÷3×60=13500（m）.

答：这船的船速是每时13.5km.

【变式】如图，某海防哨所（o）发现在它的北偏东30°距离500m的A处有一艘船。该船向正东方向航行，经过3分钟到达哨所东北方向的B处。求这艘船的航速是每时多少km？

【分析】根据上题，此时的AB有如何表示呢？

AB=BC－AC

其中AC=OA sin∠AOC=500sin30°

OC=OA cos∠AOC=500cos30°

BC=OC=500cos30°

对比两题列式的不同。

【点评】通过对比、探索、发现问题关键所在，并列出算式。在解直角三角形的教学中，要考虑数形结合的方法，弄清各相关元素之间位置关系与这些元素之间的数量关系的对应与转化，

四、小结：

在直角三角形中，当锐角一定时，它的对边与斜边、邻边与斜边、对边与邻边、邻边与对边的比值是固定的，这几个比值称为锐角的三角函数，它反映的是两条线段的比值，对于三角函数的概念，同学们必须深刻理解后再记忆，不要混淆.

【预习导学案】

（投影与视图）

一、预习前知

1. 投影的基础知识，包括投影、平行投影、中心投影、正投影等概念，正投影的成像规律；

练习：当太阳光与地面成角时，直立于地面的玲玲测得自己的影长为1.16m，则玲玲的身高约为 m. （精确到0.01m）

2. 视图、三视图等概念，三视图的位置和度量规定，一些基本几何体的三视图，简单立体图形（包括相应的表面展开图）与它的三视图的相互转化；

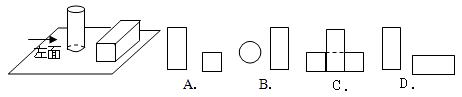
练习：桌面上放着1个长方体和1个圆柱体，按如图所示的方式摆放在一起，其左视图是（ ）

3. 课题学习：制作立体模型。这是由三视图向立体图形转化的实践活动。

练习：如图，这是一幅电热水壶的主视图，则它的俯视图是（ ）

二、预习导学

（一）选择题

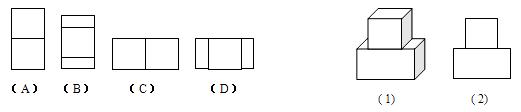
1、如图（1）放置的一个机器零件，若其主视图如图（2），则其俯视图是（ ）

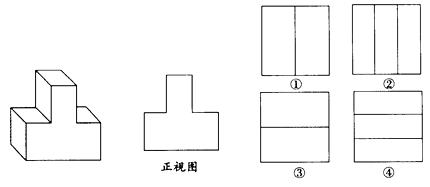
2、一物体及其正视图如下图所示，则它的左视图与俯视图分别是右侧图形中的（ ）

（A）①② （B）③② （C）①④ （D）③④

3、一个几何体的三视图如图所示，那么这个几何体是（ ）。

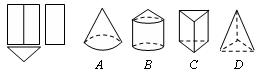
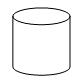
4、如图所示圆柱的左视图是（ ）.

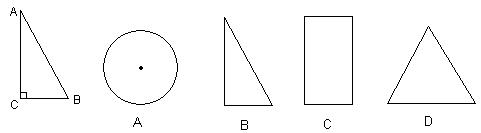
5、将下图的Rt△ABC绕直角边AC旋转一周，所得几何体的主视图是（ ）

6、下图表示一个由相同小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，那么该几何体的主视图为（ ）

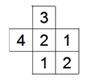
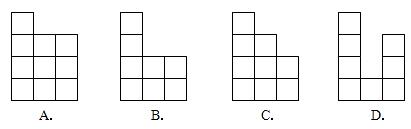
（二）填空题

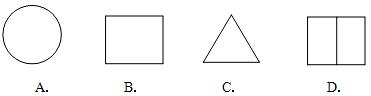
1、如果一个立体图形的主视图为矩形，则这个立体图形可能是 （只需填上一个立体图形）.

2、星期天小川和爸爸到公园散步，小川身高是160cm，在阳光下他的影长为80cm，爸爸身高180cm，则此时爸爸的影长为＿＿＿＿cm。

3、当太阳光与地面成角时，直立于地面的玲玲测得自己的影长为1.16m，则玲玲的身高约为 m. （精确到0.01m）

4、小华在距离路灯6米的地方，发现自己在地面上的影长是2米，如果小华的身高为1.6米，那么路灯离地面的高度是 米.

5、某同学的身高为1.4米，某一时刻他在阳光下的影长为1.2米，此时，与他相邻的一棵小树的影长为3.6米，则这棵树的高度为 米.

【模拟试题】（答题时间：50分钟）

一、填空题

1. △ABC中，∠C=90°，若AB=4，BC=2，则cosA=____，sinB=_____，tanA=____，cotA=________.

2. 在Rt△ABC中，∠C=90°，BC=6，sinA=，则AB=_______，sinB=________.

二、选择题

3. 在△ABC中，a=12，b=5，c=13，则sinA的值为（ ）.

A. B. C. D.

4. 已知A为锐角，tanA=，则sinA的值为（ ）.

A. B. C. D.

5. 在Rt△ABC中，∠C=90°，则下列叙述正确的是（ ）.

A. ∠A的对边与斜边的比是∠A的正弦；

B. ∠A的对边与斜边的比是∠A的余切；

C. ∠A的邻边与斜边的比是∠A的正切；

D. ∠A的对边与邻边的比是∠A的正弦

6. cotβ=，则锐角β等于（ ）.

A. 0° B. 30° C. 45° D. 60°

7. 已知Rt△ABC中，∠C=90°，cosA=，则sinA的值等于（ ）.

A. B. C. D. 1

8. 已知：如图，BC：AB=1：2，延长AB到B₁，使AB₁=2AB，延长AC到AC₁，使AC₁=2AC，则sinA的值是（ ）.

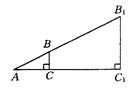
A. 1 B. C. D. 无法判断

9. 等于（ ）.

A. 1－ B. －1 C. －1 D. 1－

10. 若cot（A+10°）－3=0，则∠A的值为（ ）.

A. 40° B. 50° C. 20° D. 70°

三、简答题

11. 计算：

（1）sin30°·cos60°－sin²45°； （2）2cos60°－sin60°－│－cot30°│+.

12. 在△ABC中，若│cosA－│+（－cosB）²=0，求∠C的度数.

**13. 已知等腰三角形ABC的两边长分别为2cm，6cm，求这个等腰三角形的底角的正弦值和正切值.

14. 已知∠A为锐角，且sinA=，求tanA的值.

**15. 已知在△ABC中，A为锐角，sinA=，cosB=，且AC=10cm，求△ABC的面积.

【开放探索创新】

**16. 在△ABC中，若∠A=30°，∠C=90°，则有BC=AB. 根据勾股定理可知AC=AB，∴tanA=tan30°=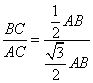=，试根据三角函数的定义，并适当添加辅助线，求出tan15°的值.

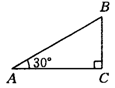
【试题答案】

1. ，，，

2. 9 点拨：根据题意画出图形，有助于增加直观性.

3. B 点拨：勾股定理及其逆定理的灵活掌握是关键.

4. A 点拨：勾股数，三角函数要灵活掌握.

5. A 点拨：三角函数的理解和掌握要结合图形，不能凭空想象.

6. D 点拨：特殊角三角函数值，不能死记硬背，可以通过特殊关系推导.

7. A

8. B 点拨：当角度固定时三角函数值即为固定值，与这个角的两边长无关.

9. B 点拨：此题的关键是二次根式的化简，判断绝对值里的值的正负.

10. C 点拨：把cot（A+10°）看作未知数，利用方程思想解题.

11. （1）原式=×－（）²=－.

（2）原式=2×－－+－1=－.

12. 由题意可知，cosA－=0且－cosB=0，

∴∠A=45°，∠B=30°，

∴∠C=180°－∠A－∠B=180°－45°－30°=105°.

**13. 由题意可知，三角形的腰为6，底为2，则如图，过A作AD⊥BC于D，由BC=2，BD=DC=1.

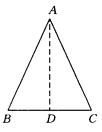
由勾股定理得AD=，

∴在Rt△ABD中，

14. 如图，在Rt△ABC中，∠C=90°，

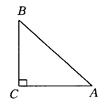
由sinA=可知，

设BC=15x，AB=17x.

∴AC=8x，

∴tanA=（方法不唯一）.

**15. ∵sinA=，∴∠A=45°，

cosB=，∴∠B=30°.

如图：

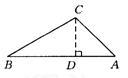
过C作CD⊥AB于D，

由∠A=45°，AC=10，

知CD=AD=5.

在Rt△BCD中，∠B=30°，CD=5.

∴BD=cot30°·CD=5，

∴AB=5+5，

∴S_△ABC=·AB·CD=（5+5）×5=25+25.

**16. 如图.

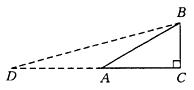
延长CA至D，使AB=AD.

∵∠BAC=30°，∠BAD=150°，

AB=AD，∴∠D=∠DBA=15°.

在Rt△ABC中，设BC=x，则AB=2x.

AC=x，则AD=2x.

所以DC=DA+AC=2x+x=（+2）x.

在Rt△DBC中，

tanD=tan15°==2－，

即tan15°=2－.