![]()
【本讲教育信息】
一. 教学内容:
格点问题
同学们,你们见过钉板吗?钉板,也就是钉着小钉的板子。板上的小钉,不管是横行还是竖行,每相邻两个小钉之间的距离都是相等的,都等于1个长度单位,就象下面这个图一样。

钉板的结构虽然简单,但是可以帮助我们解决许多复杂的数学问题。
一. 观察思考:
1. 计算下面图中各图形的面积
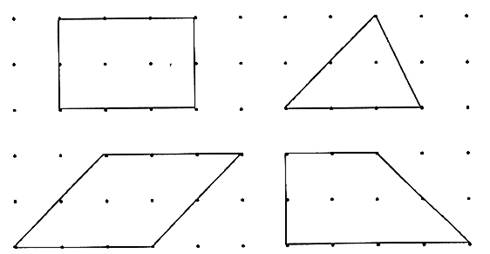
矩形面积=长×宽=![]() (单位面积)
(单位面积)
三角形面积=底×高÷![]() (单位面积)
(单位面积)
平行四边形面积=底×高![]() (单位面积)
(单位面积)
梯形面积=(上底+下底)×高÷2![]() (单位面积)
(单位面积)
2. 求下面图中三角形的面积。
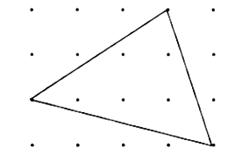
思考过程:加辅助线,将这个图形“框住”,形成一个大矩形。
三角形面积=
3. 用割、补等多种方法求图中四边形的面积。
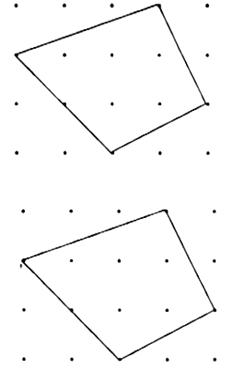
4. 计算下图中A、B两图形的面积:
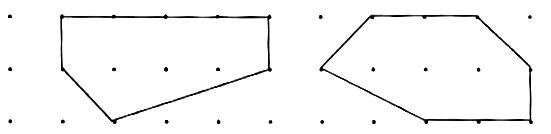
5. 找规律:
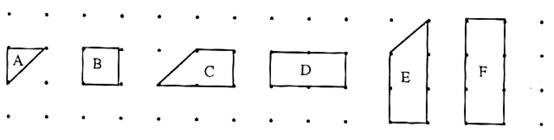
|
图形 |
外围钉数 |
内部钉数 |
面积 |
|
A |
|
|
|
|
B |
|
|
|
|
C |
|
|
|
|
D |
|
|
|
|
E |
|
|
|
|
F |
|
|
|
图形面积=外围钉数÷2-1
6. 找规律:
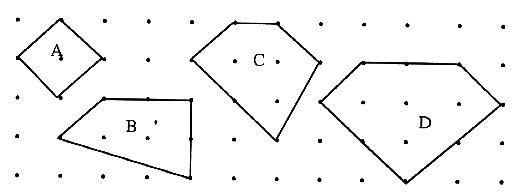
|
图形 |
外围钉数 |
内部钉数 |
面积 |
|
A |
|
|
2 |
|
B |
|
|
4 |
|
C |
|
|
5 |
|
D |
|
|
7 |
图形面积=内部钉数+外围钉数![]()
三条以上线段围成的封闭图形,称为多边形。
如果把各钉用横竖两组平行线连接起来,钉板就成了方格板,钉子就是这两组直线的交点,我们把这些点(钉子)称为格点。
如果一个多边形顶点全是格点,就称为格点多边形。
就可以用上面的公式来计算面积。
如果用S表示面积,N表示内部格点,L表示外围格点,这个公式还可以表示为
![]()
二. 尝试体验:
1. 求下图中各图形的面积。
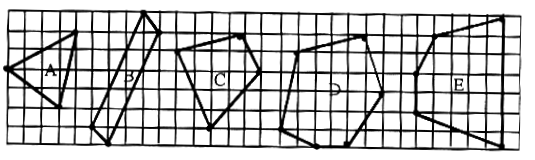
2. 用割补法求下面图形面积。
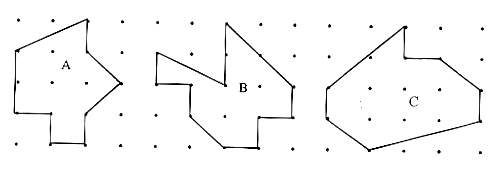
3. 求阴影部分面积是各自总面积的几分之几?
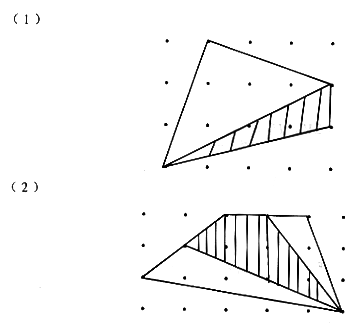
试题答案:
1. ![]()
2. ![]()
![]()
![]()
3. ![]()
(2)![]()
【模拟试题】
1、(1)如图1,在一个4×3的长方形内,△BEF的面积是( )。
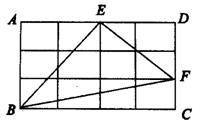
图1
(2)如图2,在一个5×3的长方形内有一个四边形,它的面积是( )。
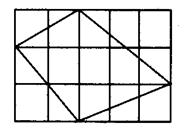
图2
(3)如图3,在一个4×6的长方形内有一个五边形,它的面积是( )。
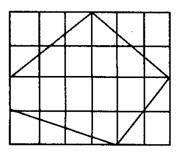
图3
(4)如图4,每个小三角形的面积为1平方厘米,则图中三角形ABC的面积是( )平方厘米。
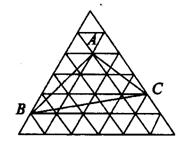
图4
2、如图5,图中每个小正方形面积都是1,图中阴影部分的面积是多少?
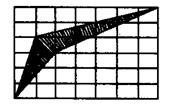
图5
3、如图6,每个小三角形的面积为1个面积单位,图中六边形的面积是多少?
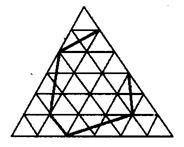
图6
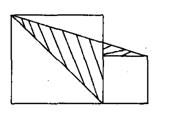
4、如图7,有两个正方形,边长8厘米和4厘米,求阴影部分的面积。
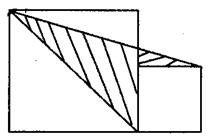
图7
5、如图8,AE=8厘米,AB=12厘米,FC=16厘米,DC=20厘米,求阴影部分的面积。
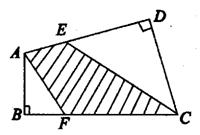
图8
![]()
【试题答案】
1、(1)5 图形内部格点数N=4,图形边上的格点数L=4,图形面积S=N+L÷2-1=4+4÷2-1=5。
(2)7.5 图形内部格点数N=6,图形边上的格点数L=5,图形的面积S=N+L÷2-1=6+5÷2-1=7.5。
(3)14 图形内部格点数N=12,图形边上的格点数L=6,图形的面积S=N+L÷2-1=12+6÷2-1=14。
(4)11平方厘米 图形内部格点数N=5,图形边上的格点数L=3,三角形ABC的面积=2×N+L-2=5×2+3-2=11(平方厘米)。
2、6.5面积单位 图形内部格点数N=5,图形边上格点数L=5,图中阴影部分面积=5+5÷2-1=6.5。
3、21面积单位 图形内部格点数N=8,图形边上格点数L=7,六边形的面积=2×N+L-2=8×2+7-2=21。
4、24平方厘米 利用大正方形边长是小正方形边长2倍的关系,将阴影部分割补成一个直角三角形,如图:则阴影部分面积为(8+4)×(8-4)÷2=24(平方厘米)。
5、176平方厘米 连AC,得到△AFC和△ACE,△AFC的面积=16×12÷2=96(平方厘米),△ACE的面积=8×20÷2=80(平方厘米),阴影部分面积为176平方厘米。