【本讲教育信息】
一、教学内容：
空间直角坐标系，包括：
1、空间直角坐标系的建立；
2、空间直角坐标系中点的坐标；
3、空间两点间的距离公式
二、学习目标
1、通过具体情境，感受建立空间直角坐标系的必要性，了解空间直角坐标系，会用空间直角坐标系刻画点的位置；
2、通过表示特殊长方体（所有棱分别与坐标轴平行）顶点的坐标，探索并得出空间两点间的距离公式；
3、经历空间直角坐标系刻画点的过程，了解类比思维，经历用代数方法刻画几何位置的过程；
4、通过在几何体中建立空间直角坐标系，进一步培养空间观念和空间想象能力；进一步了解解析几何的本质思想。
三、知识要点
一）空间直角坐标系的建立
1、空间物体位置的描述
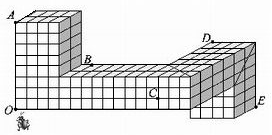
以上图为例：一只小蚂蚁站在水泥构件O点处，在A、B、C、D、E处放有食物，如何告诉小蚂蚁食物的位置？——可以结合放有食物的各点与O点的相对位置，用方位（东、西、南、北、上、下）及需要走过的距离来描述。
如：自O点出发，向东爬过5格，再向上爬过3格，再向北爬2格，即可取到放在B处的食物。
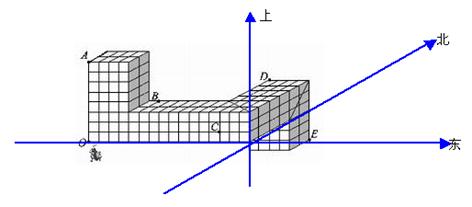
2、建立空间直角坐标系：将平面直角坐标系的x轴（横轴）和y轴（纵轴）放置在水平面上，过原点O作一条与xOy平面垂直的z轴（竖轴），这样就建立了三个维度的空间直角坐标系，如图：
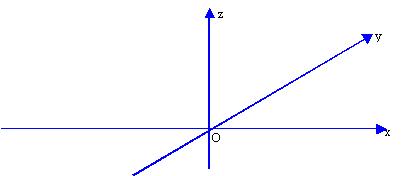
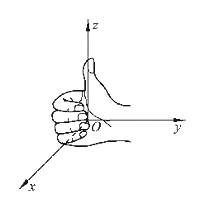
——右手系：符合右手螺旋法则，若顺着z轴看，从x轴到y轴是沿顺时针方向。
3、空间直角坐标系：空间直角坐标系中，O为坐标原点，x，y，z轴统称为坐标轴。坐标轴确定的平面称为坐标平面，x，y轴确定的平面记作xOy平面，y，z轴确定的平面记作yOz平面，x，z轴确定的平面记作xOz平面.
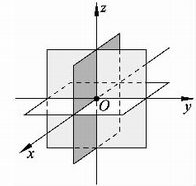
二）空间直角坐标系中点的坐标：
1、空间中点的坐标：P（x，y，z），确定方法：由P作PP＇⊥坐标平面xOy，则P＇点是平面xOy上的点，其坐标为（x，y，O），这样就确定了P的横坐标x和纵坐标y.若PP＇与z轴正半轴在平面xOy同侧，则z=|PP＇|；若PP＇与z轴正半轴在平面xOy异侧，则z=－|PP＇|，这样就确定了P点的竖坐标z。
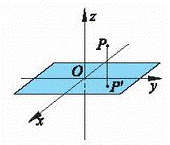
2、坐标平面上点的坐标：
①xOy平面上点的坐标：（x，y，0）；xOz平面上点的坐标：（x，O，z）；yOz平面上点的坐标：（0，y，z）；
②x 轴上点的坐标：（x，0，0）；y轴上点的坐标：（0，y，0）；z轴上点的坐标：（0，0，z）
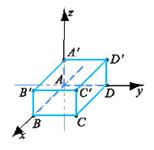
3、空间直角坐标系中长方体各顶点的坐标：设长方体ABCD－A＇B＇C＇D＇的长、宽、高分别为
，将A点放在坐标原点，AB放在x轴正半轴上，AD放在y轴正半轴上，如图：则A（0，0，0），B（a，0，0），C（a，b，0），D（0，b，0），A＇（0，0，c），B＇（a，0，c），C＇（a，b，c），D＇（0，b，c）.
三）空间两点间的距离公式
1、长方体对角线长
若长方体的长、宽、高分别为，则对角线长为
；
2、空间任意两点A（x1，y1，z1），B（x2，y2，z2），则
|AB|=
【典型例题】
考点一 建立适当的空间直角坐标系并求某些点的坐标
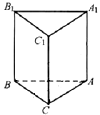
例1：如图，正三棱柱ABC－A1B1C1各棱长均为2，试建立适当坐标系，确定各顶点的坐标。
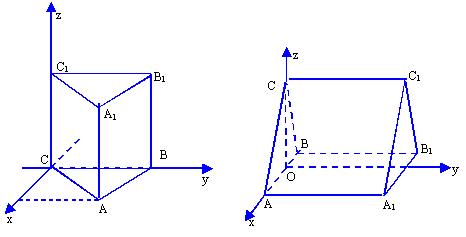
图a 图b
解：以图a为例。建立空间直角坐标系如图a。
易知，C（0，0，0），B（0，2，0），C1（0，0，2），B1（0，2，2）；
可求得：A（
），则A1（
）。
说明：建立空间直角坐标系一定要充分利用图形的垂直关系和对称关系，这样容易探求各点坐标。
考点二 空间直角坐标系中对称点的坐标
例1：已知空间中任意一点Ｐ（x，y，z），分别求Ｐ关于坐标轴、坐标平面和坐标原点对称的各点坐标。
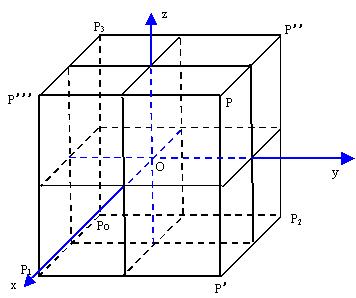
解：设空间直角坐标系中任意点Ｐ（x，y，z）．作辅助图形如上。则：
①与Ｐ关于x轴对称的点P1（x，－y，－z）；与Ｐ关于y轴对称的点P2（－x，y，－z）；与Ｐ关于z轴对称的点P3（－x，－y，z）；
②与Ｐ关于xOy平面对称的点p＇（x，y，－z）；与Ｐ关于yOz平面对称的点p''（－x，y，z）与Ｐ关于xOz平面对称的点p'''（x，－y，z）；
③与Ｐ关于Ｏ点对称的点Ｐo（－x，－y，－z）．
说明：构造长方体来研究对称点的坐标十分方便。
考点三 空间两点的距离
例3：已知A（1，2，－1），B（2，0，2），在xOz平面内的点M到A与B等距离，求M点的轨迹。
解：设M（x，y，z），由题意：|MA|=|MB|，代入两点的距离公式即得：x+3z－1=0。因此M点的轨迹是xOz平面内的一条直线。
说明：①求点的轨迹与求点的轨迹方程的区别；
②对本题中M点的轨迹进行描述时要注意到：该轨迹上的任意一点的横坐标y=0，这是平面xOz上点的特征。
考点四 空间中的直线、平面与球面方程
例4：求空间中到原点O（0，0，0）的距离为1的点M的轨迹。
解：设M（x，y，z），由题意：|MO|=1，代入坐标即得：x2+y2+z2=1。这是以O为球心、半径为1的球面。
说明：①对这种题型的处理主要结合几何意义进行直观理解和描述。
②平面xOy的方程是：z=0；平面xOz的方程是：y=0；平面yOz的方程是：x=0；
③x轴的方程是：y=z=0；y轴的方程是：x=z=0；z轴的方程是：x=y=0。
五、本讲涉及的主要数学思想方法
空间直角坐标系是研究空间点的位置的基础，空间两点的距离公式是解决空间长度的求解（甚至是空间角度的求解）的关键。建立空间直角坐标系是学习本讲的关键，要充分利用图形的垂直关系和对称关系，让尽量多的点或线落在坐标轴上或坐标平面上；对常见几何体要变换多种建系方式，对透彻了解这些几何体的性质是很有帮助的。
在学习中要充分利用好长方体这个重要模型，可以类比研究其它几何体的顶点坐标的求解或建系。另外，对平面几何中的有关结论要通过类比推广到空间中（如距离公式的推广、中点或其它分点坐标的求解、简单的直线或平面方程的求解等）。
【模拟试题】（答题时间：45分钟）
一、选择题
1、已知点（1，2，3），则该点关于x轴的对称点的坐标为（
）
A、（1，－2，－3） B、（－1，2，3）
C、（1，－2，3） D、（1，2，－3）
2、已知点P（1，2，3），则P点关于点M（3，2，1）的对称点的坐标为（ ）
A、（2，2，2） B、（－1，2，5）
C、（5，2，－1） D、（1，0，－1）
3、已知点P（1，2，3），M（x，1，2），则P，M两点间距离的最小值为（ ）
A、2 B、
C、
D、无最小值
4、在空间直角坐标系中，过点P（1，2，3）作xOz平面的垂线，则垂足M的坐标为（ ）
A、（1，2，0） B、（1，0，3） C、（0，2，3） D、（0，2，0）
5、已知A（1，－2，11），B（4，2，3），C（6，－1，4）为三角形的三个顶点，则△ABC是（ ）
A、直角三角形 B、钝角三角形 C、锐角三角形 D、等腰三角形
6、空间直角坐标系中，点P（1，2，3）到x轴的距离是（ ）
A、3 B、
C、
D、
7、已知A（1，2，－1），点C与A关于平面 xOy对称，点B与A关于x轴对称，则|BC|的长为（ ）
A、
B、4 C、
D、
二、填空题
8、已知P（1，2，3），Q（4，5，6），则线段PQ在平面xOy上的射影长为
；
9、（2008南京调研）试在平面xOy内的一条直线x+y=1上确定一点M
，使得M到点N（6，5，1）的距离最小。
三、解答题
*10、如图，以正方体的三条棱所在直线为坐标轴，建立空间直角坐标系O－xyz.点P在正方体的对角线AB上运动，点Q在正方体的棱CD上运动，已知棱长为1，求|PQ|的最小值.
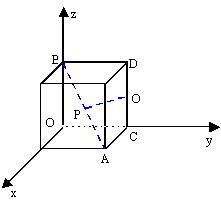
说明：该题实际上提供了求异面直线距离的一种方法——借助空间坐标，求异面直线上任意两点距离的最小值，该最小值即异面直线的距离。
11、在y轴上求一点P，使之到点M（3，－1，2）和点N（0，2，1）的距离相等.
12、设正四棱锥各棱长均为1，试建立适当的坐标系，求出各顶点的坐标.
13、证明以A（4，3，1），B（7，1，2），C（5，2，3）为顶点的三角形ABC是一等腰三角形.
【试题答案】
一、选择题：ACBBADB
二、填空题：
8、
； 9、（1，0，0）；
三、解答题
10、解：设P（x，x，z），Q（0，1，z'），则
|PQ|=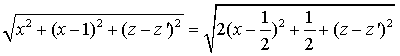
由此可知：当
同时成立时，|PQ|min=
.
11、解：设所求点P（0，y，0），依题意|PM|=|PN|，解得y=
.故所求点为P（0，，0）.
12、
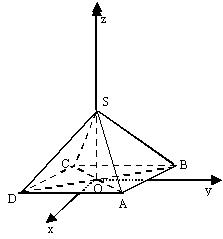
解：以底面中心O为坐标原点，建系如图.易求得：S（0，0，），A（
，，0），B（－，，0），C（－，－，0），D（，－，0）.
说明：建系不同，则所求坐标不同.
13、解：由两点间距离公式得：
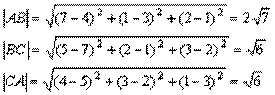
由于
，所以△ABC是一等腰三角形。