![]()
课程解读
一、学习目标:
1、掌握几何图形的概念,能分清什么是立体图形,什么是平面图形;
2、结合从不同方向看立体图形和展开立体图形,以及点、线、面、体的关系体验立体图形与平面图形的相互转化,初步建立空间观念.
二、重点、难点:
重点:掌握基本的几何概念,能够识别立体图形和平面图形.
难点:从不同方向看立体图形和展开立体图形
三、考点分析:
从近几年的中考来看,本讲主要的考点要求对空间图形有较准确的认识和感受.中考注重考查空间想象能力,从丰富的立体图形中抽象出几何体,画简单组合体的三种视图及立体图形的平面展开图,点、线、面、体及其关系.本部分内容单独命题时一般以选择题、填空题的形式出现,有时也与其他内容综合命题,约占总分的2%~4%,试题难度较小.
知识梳理
1、几何图形
(1)我们把从实物中抽象出的各种图形统称为几何图形.几何图形有立体图形和平面图形.
(2)立体图形:图形上的点不全在同一平面内.常见的立体图形有:长方体、正方体、圆柱、圆锥、球等.
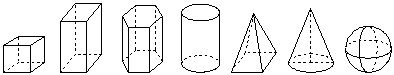
(3)平面图形:图形的各部分都在同一平面内.常见的平面图形有:线段、角、三角形、长方形、圆等.
![]()
2、立体图形和平面图形的关系
(1)从不同方向看立体图形,往往会得到不同形状的平面图形.
(2)有些立体图形是由一些平面图形围成的,将它们适当剪开,可以展开成平面图形.这样的平面图形称为相应立体图形的展开图.

3、点、线、面、体
(1)长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体.几何体也简称体.包围着体的是面.面与面相交的地方形成线.线与线相交的地方是点,它是组成几何图形的最基本的元素,一切几何图形都是由点组成的.
(2)点、线、面、体之间的关系:从运动的观点看,点动成线,线动成面,面动成体.
典型例题
知识点一:几何图形
例1. 下图所示的圆锥从上面看到的图形是( )
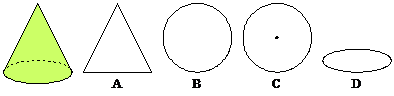
思路分析:
1)题意分析:本题考查从上面观察几何体时得到什么样的平面图形.
2)解题思路:从上面看该圆锥的大轮廓是圆,并且还可以看见圆锥的顶点.故选C,而不是B.
答案:C
解题后的思考:观察几何体时先确定大的轮廓,再注意一些小细节.
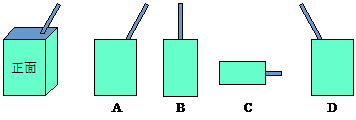
例2. 如图所示,一个斜插吸管的盒装饮料从正面看到的图形是( )
思路分析:
1)题意分析:可将要观察的饮料盒看成一个长方体,但多了一根斜插的吸管.
2)解题思路:从正面观察这个图形时,饮料盒部分看到的是长方形,注意吸管的倾斜方向.
答案:A
解题后的思考:本题可以使用排除法来解,根据吸管的倾斜方向,选项B、C、D都不正确,故选A.
例3. 如图所示是一个由立方块所搭几何体从上面看到的平面图形,正方形中的数字表示在该位置上立方块的个数,请你画出从该几何体正面和左面看到的平面图形.
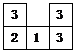
思路分析:
1)题意分析:本题考查从不同方向观察几何体.
2)解题思路:由图可知,这个几何体前后两排,左右三行.从正面看:从左到右,第一行看到第一排2个立方块和第二排最上面的一个立方块,共看到3个正方形;第二行只有第一排一个立方块,所以只能看到1个正方形;第三行前后两排各有三个立方块,只能看到前排的三个,即看到3个正方形.从左面看:第一排中可以看到第一行的两个立方块和第三行最上面的一个立方块.共看到3个正方形;第二排只能看到第一行中三个立方块,共看到3个正方形.
答案:如图所示:

解题后的思考:解答本题要有丰富的空间想象能力,把这个几何体按行和排分成若干个小的单元,采取化繁为简的方法解题.这个几何体如图所示:

例4. 如图所示,将下图的平面图形折成一个正方体,得到的是( )
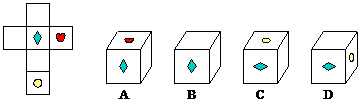
思路分析:
1)题意分析:本题要求由平面图形确定原立体图形,有一定的难度.
2)解题思路:由平面图形中的“![]() ”想象其空间关系,更有效的方法是动手操作,折一折.
”想象其空间关系,更有效的方法是动手操作,折一折.
答案:B
解题后的思考:本题容易出错,出错的原因是缺乏空间想象力,没有弄清展开图形折叠后的相对两面及相邻两面,不妨把带“![]() ”的面折放在前面,想象其他面与它的位置关系.
”的面折放在前面,想象其他面与它的位置关系.
小结:对立体图形的考查主要是从不同方向观察几何体和立体图形的表面展开图.关于用正方体堆成的几何体的问题,先把握住从上往下看到的图形,它是整个几何体的基础,再分析各部分的层数,问题便容易解决了.
知识点二:点、线、面、体
例5. 如图(1)所示,梯形绕直线旋转得到的实物图是图(2)中的( )
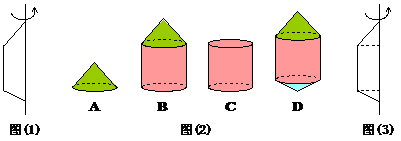
思路分析:
1)题意分析:梯形旋转时,不同的边形成不同的几何体,因此梯形旋转一周所得的几何体一定是一个复合图形.
2)解题思路:选项A是圆锥体,可以由直角三角形绕其直角边旋转得到;选项B是一个复合几何体,可看作由圆锥和圆柱组合而成,可以由直角梯形绕直角边旋转得到;选项C是圆柱体,可以由长方形绕其一边旋转得到;选项D也是一个复合几何体,可以看作由两个圆锥和一个圆柱组合而成,而图(1)是一个梯形,可以分割成如图(3)所示的两个直角三角形和一个长方形,绕轴旋转可以得到选项D中的几何体.
答案:D
解题后的思考:平面图形旋转形成几何体时,与轴同一方向的线旋转后得圆柱体,与轴成一定角度的线旋转后得圆锥.
例6. 实践与探究.
(1)用厚纸板按照下图的样子画好剪下,再把它们折起来粘好.

(2)用沙子装满粘好的硬纸盒,通过实验对比,你发现了什么结论?为什么?
思路分析:
1)题意分析:第(1)题可以粘成三个无盖的长方体盒子.第(2)题先计算三个盒子的容积,再进行比较.
2)解题思路:长方体的体积等于底面积乘高.
解答过程:(1)会形成三个无盖的长方体盒子,如图所示:

(2)通过实验可知,后两个的容积都是第一个的一半.
因为:第一个的容积是6×4×1=24(立方厘米);
第二个的容积是6×2×1=12(立方厘米);
第三个的容积是4×3×1=12(立方厘米).
解题后的思考:通过动手实验的方法探究问题的结论在科学研究中用途非常广泛,同学们应加强这方面的训练.
例7. 蛋糕店的店员包装蛋糕盒时,要用彩带捆绑,再在打结处贴一朵装饰花,请你算一算,按如图所示那样包装一个高为
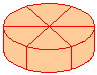
思路分析:
1)题意分析:要求的彩带的长度是几条圆柱底面圆的直径和圆柱的高的和.
2)解题思路:上底面和下底面共有6个直径、上底面和下底面之间共有6个高.
解答过程:彩带的总长:(20×2+10)×6=300(厘米).
答:最少需要
解题后的思考:要弄清彩带构成了多少条底面直径,多少条圆柱的高,再作计算.
例8. 用大小一样的小正方体搭成的几何体(其中相等的两个小正方体之间至少有一个面互相重合)从正面看到和从左面看到的平面图形如图所示,试分析探究,这样的几何体是不是只有一种?若不止一种,则最少需要多少个小正方体?最多需要多少个?

思路分析:
1)题意分析:本题只给出了从正面和从左面看到的图形,原几何体的形状不能唯一确定.
2)解题思路:结合以上两个图形,第一层从左向右,第一排有3个小正方体;第二排最少1个,最多3个;第三排最少1个,最多3个;第二层只有1个.因此,最少需要小正方体的数目为(3+1+1)+1=6(个);最多需要小正方体的数目为(3+3+3)+1=10(个).
解答过程:这样的几何体不止一种;搭成这样的几何体最少需要6个小正方体,最多需要10个小正方体.所有可能情况如图所示:

解题后的思考:要确定一个几何体的形状,需依据从正面、左面、上面看到的图形来确定,只从一个方向或两个方向来看,几何体的形状不能唯一确定.
小结:几何图形都是由点、线、面、体组成的,点是构成几何图形的基本元素.点、线、面、体经过运动变化,就能组成各种各样的几何图形.
提分技巧
1、立体图形和平面图形可以相互转化,立体图形经过从不同方向看和表面展开转化成平面图形,平面图形经过折叠和旋转转化成立体图形.
2、从运动的观点看,可以说点动成线,线动成面,面动成体.
预习导学
直线、射线、线段(4.2)
一、预习新知
1、直线、射线、线段.
2、公理.
二、预习点拨
探究与反思
探究任务一:直线、射线、线段
【反思】(1)什么是直线、射线、线段?
(2)怎样画直线、射线、线段,怎样表示它们?
探究任务二:公理
【反思】(1)什么是公理?
(2)关于直线和线段的两个公理分别是什么?
同步练习
(答题时间:60分钟)
一、选择题.
1、下列说法不正确的是( )
A.
长方体与正方体都有六个面
B.
圆锥的底面是圆
C.
棱柱的上、下底面是两个完全相同的图形
D.
三棱柱有三个面、三条棱
2、如图所示的4个立体图形中,从左边看是长方形的有( )个.
A.
0 B.
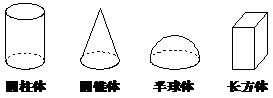
3、下列各选项中的图形绕直线l旋转一周,哪一个能得到如右图所示的立体图形.( )

4、下面四个图形中,是三棱柱的平面展开图的是( )
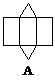
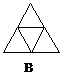

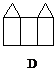
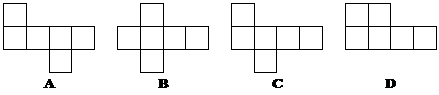
5、下列各图中不是正方体展开图的是( )
6、下左图是由若干个小正方体所搭成的几何体及从上面看这个几何体所看到的图形,那么从左边看这个几何体时,所看到的几何图形是( )
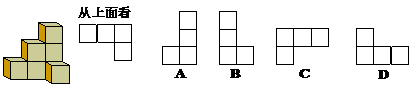
*7、一个数学玩具的包装盒是正方体,其表面展开图如下.现在每方格内都填上相应的数字.已知将这个表面展开图沿虚线折成正方体后,相对面上的两数之和为“
A.
0,-2,1 B. 0,1,-
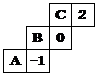
*8、如图所示的是由几个相同的小正方体搭成的几何体从不同方向看所得到的图形,则搭成这个几何体的小正方体的个数是( )个
A.
4 B.
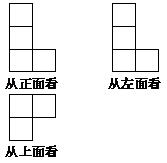
二、填空题.
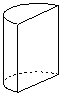
9、如图所示的立体图形,是由__________个面组成的,面与面相交成__________条直线.
10、当车上的雨刷擦过满是雨水的车窗后,将得到一部分明亮的车窗,这里包含的数学知识是__________.
11、下面是某个立体图形从三个不同的方向观察所得到的平面图形,则该物体的名称是__________.

12、一个棱柱共有12个顶点,所有的侧棱长的和是
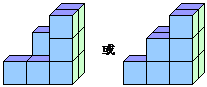
**13、下图是由一些大小相同的小正方体组成的简单几何体从正面、左面、上面看得到的图形,则组成这个几何体的小正方体的块数是__________块.

**14、一个正方体的每个面分别标有数字1、2、3、4、5、6,根据下图中该正方体A、B、C三种状态所显示的数字,可推出“?”处的数字是__________.
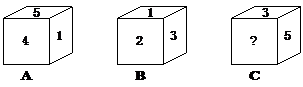
三、解答题.
15、根据下图回答问题:

(1)请说出①~⑥中几何体的名称,并简要叙述它们的一些特征.
(2)将①~⑥中的几何体分类.
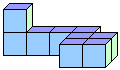
16、如图所示是一个由9个正方体组成的立体图形,分别从正面、左面、上面观察这个立体图形,各能得到什么平面图形?请画出来.
17、现有一个长为
18、下列图形都是几何体的展开图,你能说出这些几何体的名称吗?

**19、把正方体的6个面分别涂上6种不同的颜色,并画上朵数不同的花,表面上的颜色与花的朵数如下表所示:
|
颜色 |
红 |
黄 |
蓝 |
白 |
紫 |
绿 |
|
花的朵数 |
1 |
2 |
3 |
4 |
5 |
6 |
现将上述大小相同、颜色和花朵完全一样的4个正方体拼成一个水平放置的长方体.如图所示,那么长方体的下底面共有多少朵花?

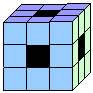
**20、如图所示,小明把一棱长为3的正方体魔方每个面正中心的一个正方形向里挖空(相当于挖去了6个小正方体),请问他所得到的几何体的表面积是多少?
![]()
试题答案
一、选择题:
1、D 解析:三棱柱有5个面,9条棱.
2、C 3、B 4、A 5、D 6、B
7、A 解析:折成正方体后,面A与0相对,面B与2相对,面C与-1相对,所以填在A、B、C内的三个数依次是0,-2,1.
8、B 解析:由从上面看所得的图形确定底层有3个小正方体,由从前面看和从左面看所得的图形可确定第二层;第三层各有1个小正方体,故共有5个小正方体.
二、填空题:
9、4,4
解析:这个立体图形的上下两个底面是半圆、侧面由一个长方形和一个曲面组成,面和面相交所成的线有直线,也有曲线,其中直线有4条.
10、线动成面
11、三棱柱 解析:这是一个倒放在水平面上的三棱柱.
12、
13、10或11,如图所示:
14、6 解析:与1相邻的四个面分别为4、5、2、3,则1的对面为6,再由B可知3的对面为4,由A可知5的对面为2,可推出“?”处的数字为6.
三、解答题:
15、解:(1)①圆柱的特征:两底面是圆;②圆锥的特征:一个底面是圆,另一“底面”缩小成一个点;③正方体的特征:所有面都是正方形;④长方体的特征:各面都是长方形(可能有两个面是正方形);⑤六棱柱的特征:两底面是六边形,侧面都是长方形(也可能是正方形);⑥球的特征:表面是一个曲面,不能展开成平面图形.(2)可分为柱体①③④⑤,锥体②,球⑥.
16、解:如图所示:
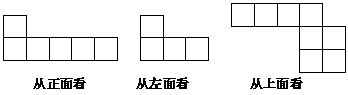
17、解:以长边为轴旋转所得圆柱体的体积是π×42×5=80πcm3;以短边为轴旋转所得圆柱体的体积是π×52×4=100πcm3.
18、解:①是正方体,②是长方体,③是圆锥,④是圆柱,⑤是五棱柱,⑥是三棱柱.
19、解:观察图形可知,黄的对面是紫,红的对面是绿,蓝的对面是白,所以长方体的下底面共有花朵:5+2+6+4=17(朵).提示:解答本题的关键是根据图形摆放出现的颜色,确定出上底面中黄、紫、红、蓝的对面(下底面)的颜色.确定方法:观察左数第四个正方体,在同一顶点处的三个面分别是蓝、黄、红,结合左数第一个和第三个正方体,黄、白相邻,红、白相邻,蓝必然和白相对;结合第二个正方体,红、紫相邻,在第四个正方体中黄必然和紫相对;则红和绿相对.
20、解:3×3×6+6×4=78.所以所得到的几何体的表面积是78.提示:得到的几何体的外部表面积等于正方体表面积减去一个小正方体的表面积,内部表面积等于六个小正方体的五个面积的面积和.也可以看作是一个大正方体的表面积与六个小正方体的四个侧面面积的和.