课程信息

 

【本讲教育信息】

一、教学内容：

本讲主要内容是简单几何体的面积与体积，包括：

1、柱、锥、台体的侧面积与表面积；

2、柱、锥、台体的体积；

3、球的表面积与体积。

 

二、学习目标

1、掌握柱、锥、台、球的表面积与体积公式；

2、了解有关侧面积公式的推导过程及其主要思想，渗透把有关立体几何问题转化为平面几何问题来解决的数学思想和类比的思想方法；

3、能用公式计算简单组合几何图形的表面积和体积；会用表面积和体积公式解决一些实际问题；

4、经历简单组合几何图形的表面积、体积计算过程，体会割补法的应用。

 

三、知识要点

（一）圆柱、圆锥、圆台的侧面积

将侧面沿母线展开在平面上，则其侧面展开图的面积即为侧面面积。

1、圆柱的侧面展开图——矩形

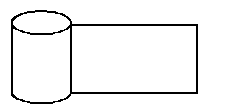
圆柱的侧面积

2、圆锥的侧面展开图——扇形

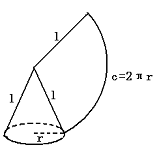
圆锥的侧面积

3、圆台的侧面展开图——扇环

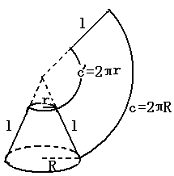
圆台的侧面积

 

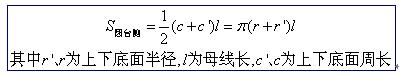
（二）直棱柱、正棱锥、正棱台的侧面积

把侧面沿一条侧棱展开在一个平面上，则侧面展开图的面积就是侧面的面积。

1、柱的侧面展开图——矩形

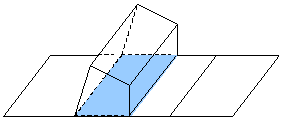
直棱柱的侧面积

2、锥的侧面展开图——多个共点三角形

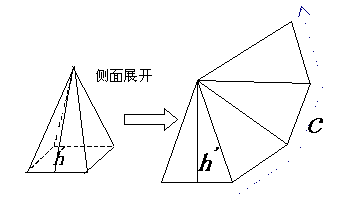
正棱锥的侧面积

3、正棱台的侧面展开图——多个等腰梯形

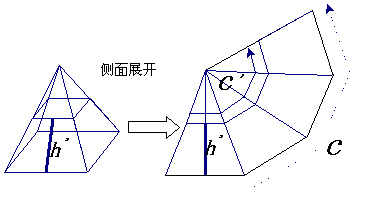
正棱台的侧面积

说明：这个公式实际上是柱体、锥体和台体的侧面积公式的统一形式

①即锥体的侧面积公式；

②c'＝c时即柱体的侧面积公式；

 

（三）棱柱和圆柱的体积

斜棱柱的体积＝直截面的面积×侧棱长

 

（四）棱锥和圆锥的体积

 

（五）棱台和圆台的体积

    

说明：这个公式实际上是柱、锥、台体的体积公式的统一形式：

①时即为锥体的体积公式；

②S上＝S下时即为柱体的体积公式。

 

（六）球的表面积和体积公式

 

（一）简单的组合几何体的表面积和体积——割补法的应用

割——把不规则的组合几何体分割为若干个规则的几何体；

补——把不规则的几何体通过添补一个或若干个几何体构造出一个规则的新几何体，如正四面体可以补成一个正方体，如图：

 

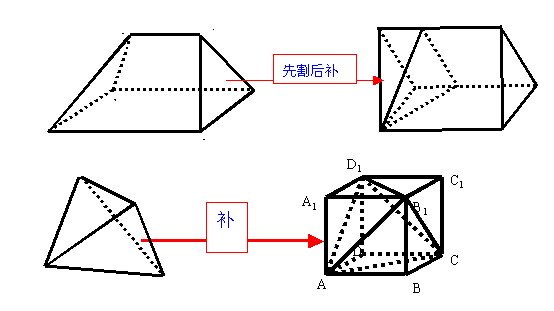
四、考点与典型例题

考点一  几何体的侧面展开图

例1. 有一根长为5cm，底面半径为1cm的圆柱形铁管，用一段铁丝在铁管上缠绕4圈，并使铁丝的两个端点落在圆柱的同一母线的两端A、D，则铁丝的最短长度为多少厘米？

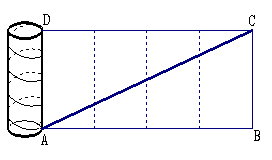
解：展开后使其成一线段AC＝

 

考点二 求几何体的面积

例2. 设计一个正四棱锥形的冷水塔顶，高是0.85m，底面的边长是1.5m，制造这种塔顶需要多少平方米铁板？（保留两位有效数字）

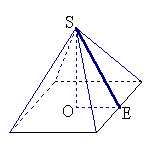
解：

答：略。

 

考点三  求几何体的体积

例3. 求棱长为的正四面体的体积。

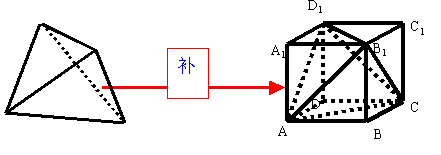
分析：将正四面体通过补形使其成为正方体，然后将正方体的体积减去四个易求体积的小三棱锥的体积。

解：如图，将正四面体补形成一个正方体，则正方体的棱长为1，则：V正四面体＝V正方体－4V三棱锥＝1－。

 

考点四  求不规则几何体的体积

例4. 证明四面体的体积，其中a，b，c为自同一顶点S出发的三条棱SA、SB、SC的长，α，β为点S处的两个面角∠BSC、∠ASC，C为这两个面所夹二面角的大小。

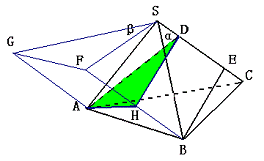
证明：通过补形，可将此三棱锥补成一个三棱柱，如图。则该三棱柱的体积可以利用“直截面面积×侧棱长”来进行求解，若设过A点的直截面为AHD，则由题意知：∠ADH＝C；

又AD⊥SC，故AD＝SA×sinβ＝a·sinβ；

若过B作BE⊥SC于E，则BE＝HD＝BC×sinα＝b·sinα.所以，

从而有

。

 

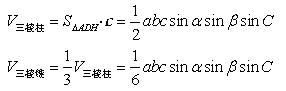考点五  球的表面积和体积

例5. 在球心的同侧有相距为9的两个平行截面，它们的面积分别为49π和400π，求球的表面积和体积。

分析：画出球的轴截面，利用球的截面性质求球的半径     

解：设球的半径为R，O为球心，O1、O2分别是截面圆的圆心，如图。

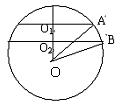
则O1A＝7，O2B＝20，OA＝OB＝R，从而分别解三角形OO2B和三角形OO1A得到OO1和OO2，由OO1－OO2＝9解得R＝25，从而

球的表面积为2500π，球的体积为。

 

考点六  求点到平面的距离——等积法的应用

例6. 在正方体ABCD－A’B’C’D’中，已知棱长为a，求B到平面AB’C的距离。

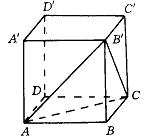
解：设B到面AB’C的距离为h，因为AB’＝B’C＝CA＝a，

所以SΔAB’C＝（a）＝a，

因此·a·h＝VB－AB′C＝ VB′－ABC ＝·a·a＝a，

故h＝a，即B到面AB′C的距离为a。

 

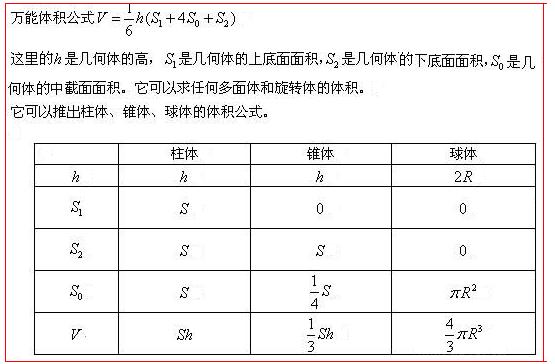
附：拟柱体通用体积公式

拟柱体：所有的顶点都在两个平行平面内的多面体叫做拟柱体.它在这两个平面内的面叫做拟柱体的底面.其余各面叫做拟柱体的侧面，两底面之间的距离叫做拟柱体的高。

，选A。

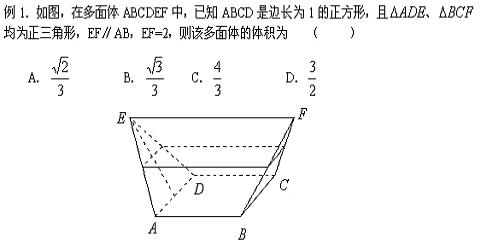
  例2. 如图所示，在多面体ABCDEF中，已知ABCD是边长为3的正方形，EF//AB，，EF与面AC的距离为2，则该多面体的体积为（    ）

    A.                    B. 5               C. 6               D.

，选D。

 

五、本讲涉及的主要数学思想方法

    计算能力是中学生要掌握的最基本的能力之一。立体几何的题型从内容上可分为两大类，一是空间位置关系的研究，二是空间量度（主要是角度与距离）的求解，也是高考命题中立体几何的两类基本题型。

    本讲主要考查空间图形的面积与体积的计算能力，对空间想象能力的要求也比较高，因为在运用公式求解之前，必须先求相关的角度与距离。要通过对几种特殊几何体的面积和体积公式的推导，掌握割补法、等积变换法等重要数学方法在解决面积与体积求解问题中的应用。所以，对空间图形的变换能力的要求较高，要通过一些典型的空间图形变换的例子，掌握变换技巧，从而化难为易，化不规则为规则，达到快速求解的目的。

 

【模拟试题】（答题时间：60分钟）

一、选择题

1. （2008四川）设M，N是球心O的半径OP上的两点，且NP=MN=OM，分别过N，M，O作垂直于OP的平面，截球面得三个圆，则这三个圆的面积之比为：（    ）

A. 3：5：6　　B. 3：6：8                C. 5：7：9            D. 5：8：9

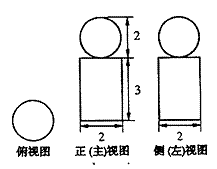
2. （2008山东）下图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（    ）

A. 9π　　　　　　　 B. 10π

C. 11π              D. 12π

3. （2008湖北）用与球心距离为1的平面去截球，所得的截面面积为，则球的体积为（    ）

A.           B.           C.           D.

4.（2008湖南）长方体ABCD－A1B1C1D1的8个顶点在同一球面上，且AB＝2，AD＝，AA1＝1，则顶点A、B间的球面距离是（      ）

A. 2             B.         C.         D.

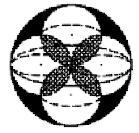
*5. （2008重庆）如图，体积为V的大球内有4个小球，每个小球的球面过大球球心且与大球球面有且只有一个交点，4个小球的球心是以大球球心为中心的正方形的4个顶点.V1为小球相交部分（图中阴影部分）的体积，V2为大球内、小球外的图中黑色部分的体积，则下列关系中正确的是（    ）

A. V1＝                                               B.  V2＝

C. V1> V2                                             D. V1< V2

6. （2008海南改）一个六棱柱的底面是正六边形，其侧棱垂直于底面。已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为，底面周长为3，那么这个球的体积为 （    ）

A.            B.        C.        D.

7. （2008天津改）若一个球的体积为，则它的表面积为（   ）

A.     B.     C. 12    D. 24

 

二、填空题：

8.（2008四川）已知正四棱柱的对角线的长为，且对角线与底面所成角的余弦值为，则该正四棱柱的体积等于________________。

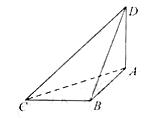
9. （2008浙江）如图，已知球O的面上四点A、B、C、D，DA平面ABC，ABBC，DA＝AB＝BC＝，则球O的体积等于___________。

 

三、解答题

*10.（2008广东卷）

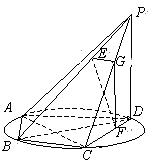
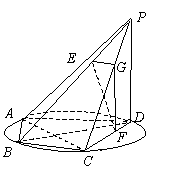
如图所示，四棱锥的底面是半径为的圆的内接四边形，其中是圆的直径，，，垂直底面，，分别是上的点，且，过点作的平行线交于．

（1）求与平面所成角的正弦值；

（2）证明：是直角三角形；

（3）当时，求的面积。

 

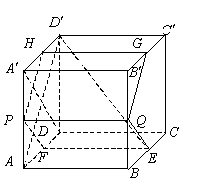
11.（2008辽宁卷）

如图，在棱长为1的正方体中，AP＝BQ＝b（0<b<1），截面PQEF∥，截面PQGH∥。

（Ⅰ）证明：平面PQEF和平面PQGH互相垂直；

（Ⅱ）证明：截面PQEF和截面PQGH的面积之和是定值，并求出这个值；

（Ⅲ）若与平面PQEF所成的角为，求与平面PQGH所成角的正弦值。

**12. 在六条棱分别为2，3，3，4，5，5的所有四面体中，最大的体积是多少？并证明你的结论。

13. 设一直角四面体P－ABC（即∠APB＝∠BPC＝∠CPA＝90º）的三条棱PA、PB、PC的长之和为L，试求（并证明）其最大体积。

 

【试题答案】

一、选择题    DDBCD  AC

 

二、填空题

8、2；

9、

 

三、解答题

10、【解】（1）在中，，

而PD垂直于底面ABCD，

，

在中，，即为以为直角的直角三角形。

设点到面的距离为，由有，即

     ；

（2），而，即，

，是直角三角形；

（3）时，，

即，

的面积

11、解：

（Ⅰ）证明：在正方体中，，，又由已知可得，，，所以，，所以平面。

所以平面和平面互相垂直。

（Ⅱ）证明：由（Ⅰ）知，又截面PQEF和截面PQGH都是矩形，且PQ＝1，所以截面PQEF和截面PQGHR的 面积之和是

，是定值。

（III）解：连结BC′交EQ于点M。

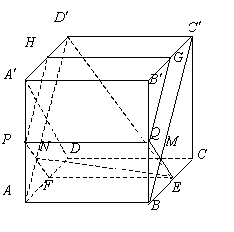
因为，，

所以平面和平面PQGH互相平行，因此与平面PQGH所成角与与平面所成角相等．

与（Ⅰ）同理可证EQ⊥平面PQGH，可知EM⊥平面，因此EM与的比值就是所求的正弦值．

设AD’交PF于点N，连结EN，由知

．

因为AD’⊥平面PQEF，又已知与平面PQEF成角，

所以，即，

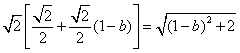解得，可知E为BC中点．

所以EM＝，又，

故D’E与平面PQGH所成角的正弦值为．

  12、【解】三角形两边之和大于第三边，按题设的数据，一边为2的三角形，其余两边只可能是：①3，3；②5，5；③4，5；④3，4。

从而，四面体中以2为公共边的有两个面，其余两边只可能有下列三种情形：1．①与②；2．①与③；3．②与④．

下面就这三种情形分别讨论．

1. 如图a，由勾股定理，CD⊥AC，CD⊥BC，所以，四面体的体积

2. 如图b、c，这样的四面体有两个，它们的体积为

   

 

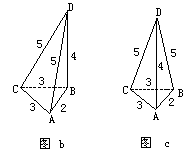
3. 如图d、图e，这样的四面体也有两个，体积为

    

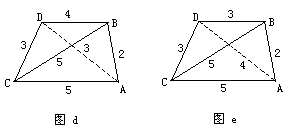
13、设一直角棱长为x，一直角棱长为y，则第三条直角棱长为L－x－y，则体积，等号当且仅当x＝y＝L－x－y时成立，从而。