![]()
【本讲教育信息】
一. 教学内容:
1、圆锥的认识
2、圆锥的体积
二、教学重点和教学难点:
圆锥的认识
教学重点:
1、认识圆锥的各部分名称及其特征,会测量圆锥的高.
2、学生经历猜想、比较、观察、分析、反思等活动,从而真正理解、认识圆锥的高,进一步掌握圆锥的特征,培养学生动手操作能力和空间观念并使学生掌握研究几何形体时常用的一些方法.
教学难点:
1、圆锥的高的认识
2、空间观念的形成
圆锥的体积
教学重点:
1、通过实验,使学生理解并掌握圆锥的体积公式,能运用体积公式正确的进行计算.
2、培养学生的观察,动手操作的能力以及空间想象能力.
教学难点:
1、理解和掌握圆锥体积的计算公式
2、掌握圆柱和圆锥体积之间的关系
三、简要知识介绍:
圆锥知识的学习包括圆锥的认识和圆锥的体积两部分,是在学生掌握了圆和圆柱的相关知识的基础上进行教学的.
圆锥认识的学习体系同圆柱的认识是相同的,既有圆锥的特征又有各部分名称.学习中对高的认识是这部分的难点,高是指圆锥的顶点到底面圆心的距离是圆锥的高.
圆锥体积的计算,学习的重点是体积公式的推导过程.只有等底等高的圆柱、圆锥,才具有圆柱的体积是圆锥体积的3倍,圆锥体积是圆柱的这样的关系.
当然,我们也可以进行这样的类推:
圆柱、圆锥在底面积相等、高相等的情况下,圆柱体积是圆锥的3倍.
圆柱、圆锥在体积、高相等的情况下,圆锥的底面积是圆柱底面积的3倍.
圆柱、圆锥在体积相等,底面积相等的情况下,圆锥的高是圆柱的高的3倍.
[知识教学]
一、圆锥的认识
(一)引入:
1、谈话:我们在对圆柱的学习中,采取了哪些研究的方法?(看、量、比、剪).
我们都研究了圆柱的哪些知识?(认识、表面积、体积)
2、圆锥的形成:
(1)我们在研究圆柱体时,把一个长方形硬纸贴在木棒上,快速转动,可以形成一个圆柱体.

思考:如果是一个直角三角形,以直角边为轴旋转,转出来会是什么形状呢?(圆锥)
(2)同学们,在日常生活中你们都见过哪些圆锥形状的物体?

(二)圆锥的特征
1、初步认识
圆锥的底面是个圆形,侧面展开是个扇形,有1个顶点……
圆锥的高:顶点到底面圆心的距离是圆锥的高.
圆锥只有一条高
高的测量:
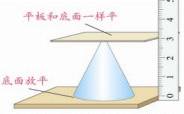
2、加深对高的理解
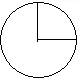
将这个圆像上面这样分成两个扇形,扇形的半径是相等的,同学们可以猜想做好的两个圆锥的高一样吗?

3、画圆锥的示意图
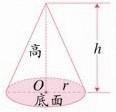
4、从不同角度看圆锥.
判断是从哪个角度对圆锥进行观察的?
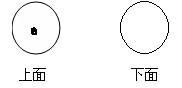
5、小结
|
|
圆柱 |
圆锥 |
|
示意图 |
|
|
|
特征 |
有2个底面,1个侧面,2个底面是相等的圆. |
有1个侧面,1个底面,底面是圆形. |
|
高 |
高是两底面之间的距离. 有无数条高. |
从圆锥的顶点到底面圆心的距离是圆锥的高. 有1条高. |
|
旋转体 |
|
|
|
研究方法 |
看、量、比、剪 |
|
二、圆锥的体积
1、计算公式的推导
通过实验,发现等底等高的圆锥、圆柱的体积有什么关系?你能用字母表示出它们的关系吗?
![]()
追问:如果我们知道圆锥的底面半径、直径或者周长时,都该怎样求它的体积?
知半径:πr2h=V
知直径:先计算半径,再计算体积
知道周长:同上
2、解决问题
(1)工地上有一些沙子,堆起来近似于一个圆锥,这堆沙子大约有多少立方米?(得数保留两位小数)
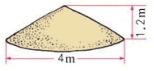
半径:4÷2=2(米)
体积:×2×2×3.14×1.2=5.024(立方米)≈5.02(立方米)
答:这堆沙子大约是5.02立方米.
(2)看图计算圆锥的体积
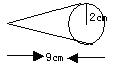
解:22×3.14×9×1/3=37.68(立方厘米)
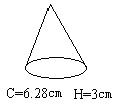
(6.28÷3.14÷2)2×3.14×1/3×3=3.14(立方厘米)
小结:无论题目中给了什么条件,都要先转化成底面积,再进行计算.
强调:在什么情况下,圆柱和圆锥的体积才具有这样的关系?(底面积相等、高相等)
三、圆锥与圆锥、圆柱与圆锥之间的关系.
1、圆锥与圆锥之间的关系
如果圆锥的半径扩大2倍,高不变,体积扩大(4)倍.
如果圆锥的半径不变,高扩大2倍,体积扩大(2)倍.
如果圆锥的半径扩大2倍,高缩小2倍,体积扩大(2)倍.
2、圆柱和圆锥之间的关系
思考:
(1)当圆锥和圆柱的底面积相等,体积也相等,它们的高有什么关系?
(2)当圆柱和圆锥的高相等,体积也相等的时候,它们的底面积有什么关系?
小结:
(1)等底,等高的圆锥和圆柱,柱的体积是锥的3倍,锥的体积是柱的1/3
(2)等体,等底的圆锥和圆柱,柱的高是锥的1/3,锥的高是柱的3倍
(3)等体,等高的圆锥和圆柱,柱的底面积是锥的1/3,锥的底面积是柱的3倍
3、关系应用
(1)在一个圆柱中削一个最大的圆锥,你能发现圆柱和圆锥体积之间存在什么关系吗?

还能想到:圆柱的体积是3份,圆锥的体积是1份,削去的部分是2份
例:把一个圆柱削成一个最大的圆锥,削去的体积是74.4立方厘米,削成的圆锥的体积是(37.2)立方厘米. 74.4÷2=37.2(立方厘米)
(2)有一个近似圆柱形的金属零件(如下图),如果把它熔化成一个和它等底的圆锥体,圆锥体的高是多少?

方法一:圆柱的体积与圆锥的体积相等
33×1.5=49.5(立方分米)
49.5×3÷33=4.5(分米)
方法二:圆柱、圆锥是体积、底面积相等的关系,圆锥的高是圆柱的高的3倍.
1.5×3=4.5(分米)
(3)在正方体中削一个最大的圆柱,圆柱的体积占正方体体积的78.5%,如果在正方体中削一个最大的圆锥,圆锥的体积占正方体的百分之几?
78.5%÷3 ≈
26.2%
【模拟试题】(答题时间:30分钟)
1、判断下列各图哪些是圆锥.
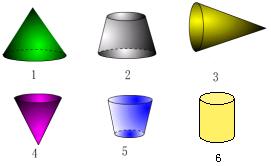
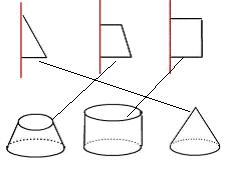
2、下列图形以红线为轴旋转后会形成什么图形,连一连.
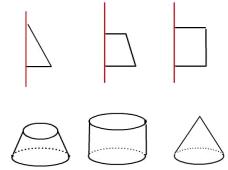
3、填表练习:
|
底面积(平方米) |
高(米) |
圆柱体积(立方米) |
圆锥体积(立方米) |
|
6 |
0.5 |
|
|
|
|
2 |
|
12 |
|
10 |
|
9 |
|
4、填空 :
(1)一个圆柱和一个圆锥等底等高,圆柱的体积是圆锥体积的( )倍.
(2)有一个圆柱和一个圆锥,它们的底面半径相等,高也相等,圆柱的体积是6立方厘米,圆锥的体积是( )立方厘米.
(3)一个圆柱和一个圆锥,他们的底面直径相等,高也相等,圆锥的体积是18立方分米,圆柱的体积是( )立方分米.
(4)一个圆柱体和一个圆锥体等底、等高,已知圆柱体和圆锥体的体积相差6立方厘米.圆柱体和圆锥体的体积分别是( )和( ).
(5)一个高是5厘米的圆柱容器里盛满水,把水倒入和这个圆柱等底等体的圆锥形容器里,水面的高度是( )厘米.
(6)一个圆锥体的底面直径是圆柱体底面直径的3倍,如果它们的高相等,那么圆锥体的体积是圆柱体体积的( )倍.
5、解决问题
(1)一堆煤堆成圆锥状,底面半径是1.5米,高是1.2米,每立方米的煤约重1.4吨,这堆煤共重多少吨?(得数保留整数)
(2)一个圆锥雕塑的体积是3立方米,它的占地面积是3平方米,这个雕塑高多少米?
(3)工厂要生产等底等高的圆柱、圆锥零件,已知一个圆柱零件和圆锥零件的体积和是42立方分米,你知道圆柱和圆锥的体积分别是多少吗?
(4)把一个体积为25.12立方米的圆锥钢材,融化成一个底面半径为2米的圆柱钢材,圆柱形钢材的高是多少分米?
![]()
【试题答案】
1、判断下列各图哪些是圆锥.
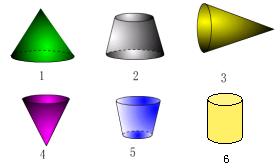
(1、3、4号是圆锥)
2、下列图形以红线为轴旋转后会形成什么图形,连一连.
3、填表练习:
|
底面积(平方米) |
高(米) |
圆柱体积(立方米) |
圆锥体积(立方米) |
|
6 |
0.5 |
3 |
1 |
|
18 |
2 |
36 |
12 |
|
10 |
0.9 |
9 |
3 |
4、填空:
(1)一个圆柱和一个圆锥等底等高,圆柱的体积是圆锥体积的(3)倍.
(2)有一个圆柱和一个圆锥,它们的底面半径相等,高也相等,圆柱的体积是6立方厘米,圆锥的体积是(2)立方厘米.
(3)一个圆柱和一个圆锥,他们的底面直径相等,高也相等,圆锥的体积是18立方分米,圆柱的体积是(54)立方分米.
(4)一个圆柱体和一个圆锥体等底、等高,已知圆柱体和圆锥体的体积相差6立方厘米.圆柱体和圆锥体的体积分别是(9立方厘米)和(3立方厘米).
(5)一个高是5厘米的圆柱容器里盛满水,把水倒入和这个圆柱等底等体的圆锥形容器里,水面的高度是(15)厘米.
(6)一个圆锥体的底面直径是圆柱体底面直径的3倍,如果它们的高相等,那么圆锥体的体积是圆柱体体积的(3)倍.
5、解决问题
(1)一堆煤堆成圆锥状,底面半径是1.5米,高是1.2米,每立方米的煤约重1.4吨,这堆煤共重多少吨?(得数保留整数)
×1.5×1.5×3.14×1.2×1.4≈4(吨)
答:这堆煤共重4吨.
(2)一个圆锥雕塑的体积是3立方米,它的占地面积是3平方米,这个雕塑高多少米?
3÷÷3=3(米)
答:这个雕塑高
(3)工厂要生产等底等高的圆柱、圆锥零件,已知一个圆柱零件和圆锥零件的体积和是42立方分米,你知道圆柱和圆锥的体积分别是多少吗?
42÷(1+3)=10.5(立方分米)
10.5×3=31.5(立方分米)
答:圆柱的体积是31.5立方分米,圆锥的体积是10.5立方分米.
(4)把一个体积为25.12立方米的圆锥钢材,融化成一个底面半径为2米的圆柱钢材,圆柱形钢材的高是多少分米?
25.12÷(2×2×3.14)=2(米)
答:圆柱形钢材的高是20分米.