【本讲教育信息】
一. 教学内容：
空间几何体
二. 教学目标：
1、认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实世界中简单物体的结构，了解柱、锥、台、球的概念。
2、了解画立体图形三视图的原理，并能画出简单几何图形（长方体、球、圆柱、圆锥、棱柱等简易组合）的三视图。能识别上述三视图所表示的立体模型，会用斜二测法画出立体图形的直观图。
［教学过程］
一. 知识要点
仔细观察下列几何体，它们有什么共同特点？
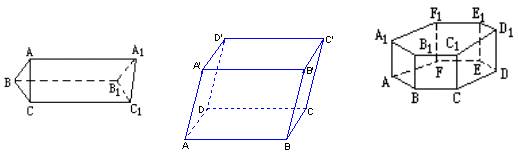
1、棱柱
一般地，由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱。
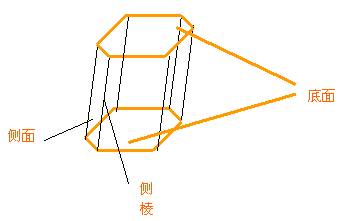
棱柱的性质：
棱柱的两个底面是全等的多边形，且对应边互相平行，侧面都是平行四边形。
2、棱锥
当棱柱的一个底面收缩为一个点时，得到的几何体叫棱锥。
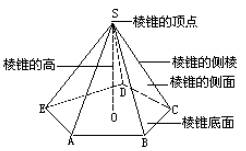
棱锥的特点：底面是多边形，各侧面是有一个公共顶点的三角形。
3、棱台
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分是棱台。
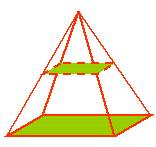
棱台的特点：
（1）侧面是梯形
（2）两底是相似多边形
4、圆柱、圆锥、圆台
将矩形、直角三角形、直角梯形分别绕着它的一边、一直角边、垂直于底边的腰所在的直线旋转一周，形成的几何体分别叫做圆柱、圆锥、圆台。这条线叫做轴，垂直于轴的边旋转而成的圆面叫做底面，不垂直于轴的边旋转而成的曲面叫做侧面，无论旋转到什么位置这条边都叫做母线。
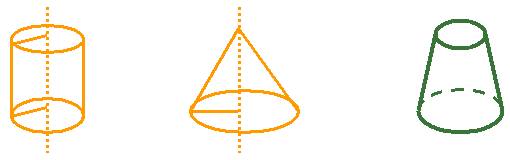
圆柱的特点：
（1）两底互相平行且相等，平行底的截面是与底相等的圆。
（2）所有的母线都相等且平行，并与底垂直。
（3）通过轴的截面是以底为直径和母线为邻边的矩形（叫做圆柱的轴截面）。
圆锥的特点：
（1）所有母线都相等。
（2）通过轴的截面是以母线为腰、底圆直径为底的等腰三角形（叫做圆锥的轴截面）。
圆台的特点：
通过轴的截面是以上、下底直径为底、母线为腰的等腰梯形。
5、球
以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体。
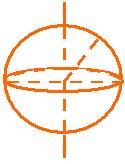
二、中心投影和平行投影
1. 投影是光线通过物体,向选定的面投射,并在该面上得到图形的方法.
这里的光线称为投影线，被选定的面称为投影面。
2. 常见的两种投影方式：中心投影与平行投影
定义：投影线交于一点的投影称为中心投影。
定义：投影线互相平行的投影称为平行投影。
平行投影的分类：
按投影方向是否正对着投影面,可以把平行投影分为正投影与斜投影。
重要概念： 三视图
将物体按正投影向投影面投影所得到的图形，称为视图。
线自物体的前面向后投射所得的投影称为主视图或正视图，自上向下的称为俯视图，自左向右的称为左视图。
用这三种视图刻画空间物体的结构，称为三视图。
说明：
1. 我们从不同的方向观察同一物体时，可能看到不同的图形。其中，把从正面看到的图叫做正视图，从左面看到的图叫做左视图，从上面看到的图叫做俯视图。
2. 画物体的三视图时,要符合如下原则：
位置：正视图 侧视图
俯视图
大小：长对正,高平齐,宽相等
三、斜二测画法
直观图：把空间图形画在平面内，使得既富有立体感，又能表达出图形各主要部分的位置关系和度量关系的图形。
水平放置图形斜二测画法规则：
（1）在已知图形中取互相垂直的x轴、y轴。画直观图时，把它画成对应的x′轴、y′轴，使∠x′O′y′=45°（或135°）．它们确定的平面表示水平平面。
（2）已知图形中平行于x轴或y轴的线段，在直观图中分别画成平行于x′轴或y′轴的线段。
（3）已知图形中平行于x轴的线段，在直观图中保持原长度不变；平行于y轴的线段，长度为原来的一半。”
【典型例题】
例1. 画水平放置的边长为
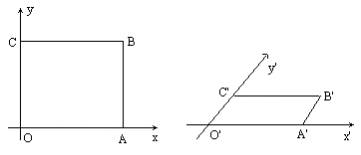
画法：
（1）在已知正方形OABC中，取OA所在的直线为x轴，取OC所在的直线为y轴，画对应的x′轴、y′轴，使∠x′O′y′=45°。
（2）在x′轴截取O′A′= OA，在y′轴上截取O′C′=
OC
（3）过A′点作A′B′
O′C′，连C′B′，则O′A′B′C′就是正方形OABC的直观图。
例2. 画出此物体的三视图
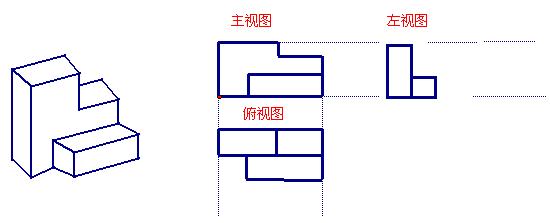
例3. 画出下列物体的三视图
解：
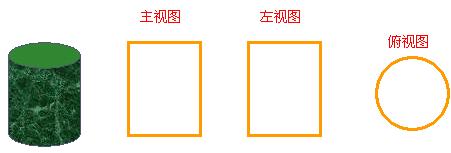
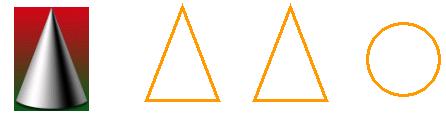
例4. 画棱长为
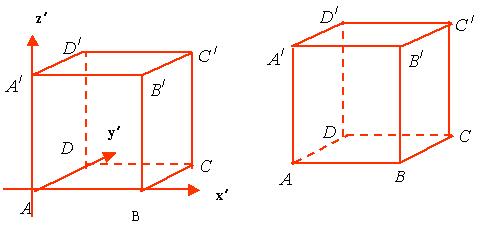
画法：
第一步：作水平放置的正方形直观图ABCD，使
=
，AB=
第二步：过A作z′轴，使
=
，分别过点B，C，D作z′轴的平行线，在z′轴及这组平行线上分别截取AA′=B B′=C C′=D
D′=
第三步：连结A′B′，B′C′，C′D′，D′A′。
斜二测画法规则：
（1）在已知图形中取互相垂直的x轴、y轴。再过交点O截取z轴，使
画直观图时，把它画成对应的x′轴、y′轴，使∠x′O′y′=45°（或135°）。它们确定的平面表示水平平面。
（2）已知图形中平行于x轴、y轴、z轴的线段，在直观图中分别画成平行于x′轴、y′轴，z′轴的线段。
（3）已知图形中平行于x轴和z轴的线段，在直观图中保持原长度不变；平行于y轴的线段，长度为原来的一半。
例5. 已知一四边形ABCD的水平放置的直观图是一个边长为2的正方形，请画出这个图形的真实图形。
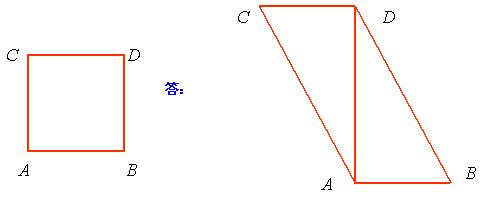
【模拟试题】（答题时间：20分钟）
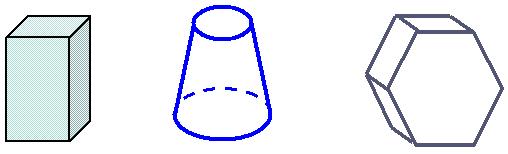
1.画出下列基本几何体的三视图
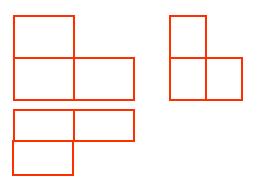
2. 你能根据下面的三视图画出它的原立体图形吗?
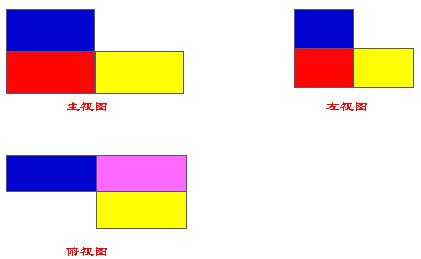
3. 下面是一个组合图形的三视图，请描述物体形状
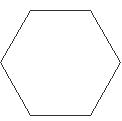
4. 画水平放置的正六边形的直观图
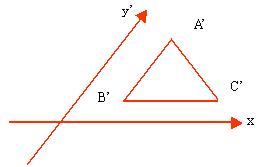
5. 下图是ΔABC利用斜二测画法得到的水平放置的直观图ΔA’B’C’，其中A’B’∥y’轴，B’C’∥x’轴，若ΔA’B’C’的面积是3，则ΔABC的面积是（ ）
【试题答案】
1.
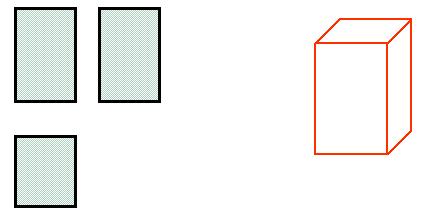
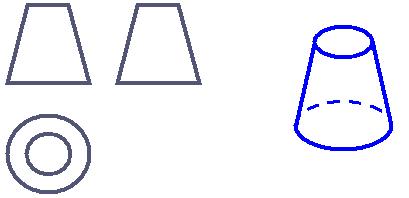
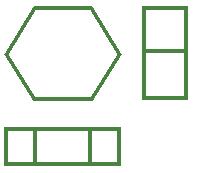
2.
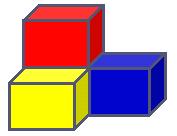
3.
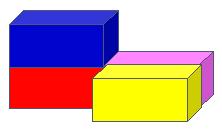
4.
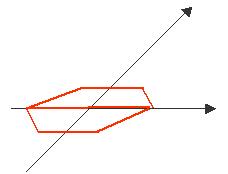
5. 