![]()
【本讲教育信息】
一. 教学内容:
简单几何体、直观图与三视图
1、简单旋转体与简单多面体;
2、直观图;
3、简单组合体的三视图;
4、由三视图还原成实物图
二. 学习目标
1、了解简单旋转体和简单多面体的有关概念;
2、了解空间图形的不同表现形式,直观地了解空间图形在平面上的表示方法;
3、会用斜二测画法画水平放置的平面图形的直观图和长方体、正方体的直观图;
4、会画正棱锥、正棱柱和圆柱的直观图;
5、进一步掌握在平面上表示空间图形的方法和技能;
6、能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别三视图所表示的立体模型,会使用材料(如纸板)制作模型。
三. 知识要点
(一)简单旋转体
1、旋转面:一条平面曲线绕着它所在平面内的一条定直线旋转所形成的曲面叫作旋转面。
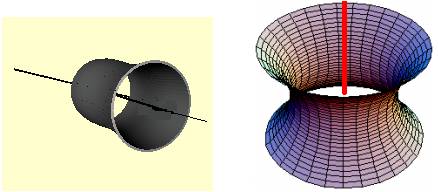
2、旋转体:封闭的旋转面围成的几何体叫作旋转体。
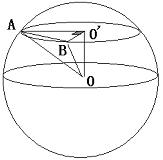
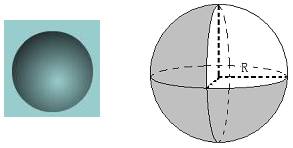
3、球:以半圆的直径所在的直线为旋转轴,将半圆旋转所形成的曲面叫作球面。球面所围成的几何体叫球体,简称球。半圆的圆心叫球心,连接球心和球面上任一点的线段叫作球的半径。连接球面上两点且过球心的线段叫作直径。过球心的截面与球面的交线称为大圆,其它的截面与球面的交线称为小圆。大圆夹在球面上两点之间的劣弧的长称为两点的球面距离,两点的球面距离是球面上经过这两点的距离的最小值。
4、圆柱、圆锥、圆台:分别以矩形的一边、直角三角形的一条直角边、直角梯形垂直于底边的腰所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体分别叫作圆柱、圆锥、圆台。
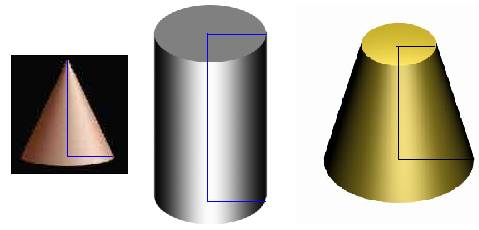
在旋转轴上这条边的长度叫作它们的高,垂直于旋转轴的边旋转而成的圆面叫作它们的底面,简称底,不垂直于旋转轴的边旋转而成的曲面叫作它们的侧面,无论转到什么位置,这条边都叫作侧面的母线。
圆台也可以看作是用平行于圆锥底面的平面截这个圆锥而得到。
5、圆柱、圆锥、圆台都是旋转体。
(二)简单多面体
我们把若干个平面多边形所围成的几何体叫作多面体。其中棱柱、棱锥、棱台是简单多面体。
1、棱柱:
①两个面互相平行,其余各个面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫作棱柱。
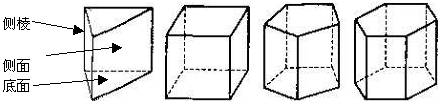
这里的两个互相平行的面叫作棱柱的底面,其余的各面叫作棱柱的侧面,棱柱的侧面是平行四边形。
两个面的公共边叫作棱柱的棱,其中两个侧面的公共边叫作棱柱的侧棱,底面多边形与侧面的公共顶点叫作棱柱的顶点,与两个底面都垂直的直线夹在两底面间的线段长叫作棱柱的高。
②侧棱不垂直于底面的棱柱叫作斜棱柱,侧棱垂直于底的棱柱叫作直棱柱,底面是正多边形的直棱柱叫作正棱柱。
棱柱的底面可以是三角形、四边形、五边形……我们把这样的棱柱分别叫作三棱柱、四棱柱、五棱柱……
2、棱锥:
①有一个面是多边形,其余各面是有一个公共顶点的三角形,这些面所围成的几何体叫作棱锥。这个多边形叫作棱锥的底面,其余各面叫作棱锥的侧面。相邻两个侧面的公共边叫作棱锥的侧棱,各侧面的公共点叫作棱锥的顶点,过顶点作底面的垂线,顶点与垂足间的线段长叫作棱锥的高。

②如果棱锥的底面是正多边形,且各侧面全等,就称作正棱锥。正棱锥的侧面是全等的等腰三角形,它底边上的高叫作正棱锥的斜高(如上图A中的SH)。
3、棱台:
①用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台。原棱锥的底面与截面叫作棱台的下底面和上底面,其它各面叫作棱台的侧面,相邻侧面的公共边叫作棱台的侧棱,与两个底面都垂直的直线夹在两底面间的线段长叫作棱台的高。
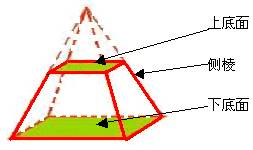
②用正棱锥截得的棱台叫作正棱台。正棱台的侧面是全等的等腰梯形,它的高叫作正棱台的斜高。
③类似于棱柱,棱锥和棱台也有三棱锥、四棱锥和三棱台、四棱台等。
三棱锥也叫作四面体。
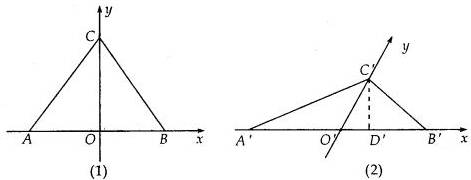
(三)水平放置的平面图形的直观图的画法——斜二测画法
画法规则:1、在已知图形中建立直角坐标系xOy,画直观图时,它们分别对应x′,y′轴,两轴交于点O′,使∠x′O′y′=45°,它们确定的平面表示水平面;
2、已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x'轴或y'轴的线段;
3、已知图形中平行于x轴的线段在直观图中保持原长度不变;平行于y轴的线段,在直观图中长度为原来的一半。
(四)三视图
1、三视图欣赏
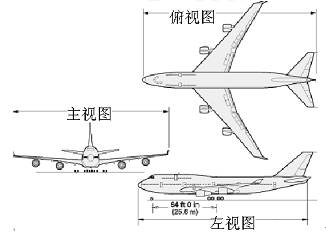
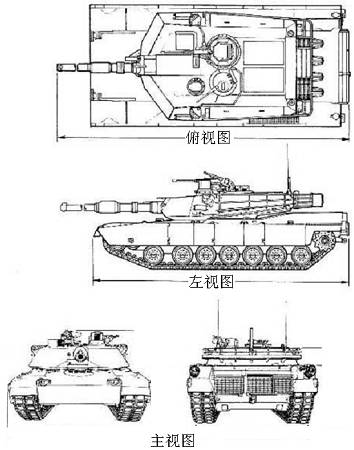
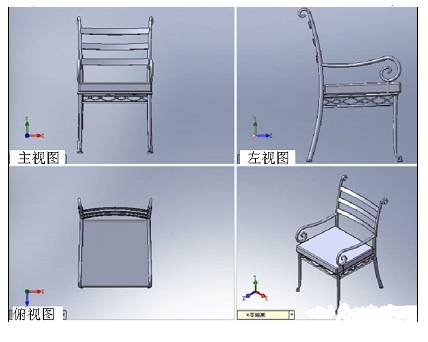
2、几何组合体的组合形式:
(1)将基本几何体拼接成组合体——叠加
(2)从基本几何体中切掉或挖掉部分构成——挖切
一般地,组合体是由上述两种方式综合构成的。
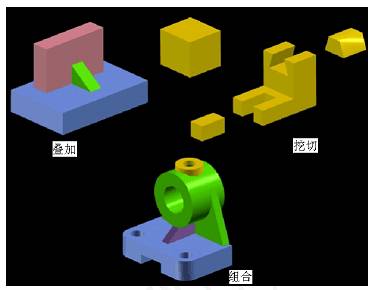
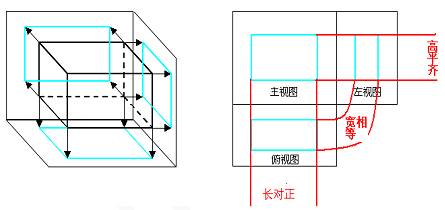
3、三视图的特点:长对正——主、俯视图反映了物体的长;高平齐——主、左视图反映了物体的高;宽相等——俯、左视图都反映了物体的宽,而且前后对应。
4、三视图的画法步骤:
(1)先确定主视图的位置,分析几何体的构造,画主视图;
(2)按“长对正”原则画俯视图;一般地,俯视图画在主视图的正下方;
(3)按“高平齐”原则画左视图;并注意左视图与俯视图“宽相等”;一般地,左视图画在主视图的正右方。
注意:①若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,分界线和可见轮廓线都用实线画出;
②不可见轮廓线用虚线画出
5、由三视图还原成实物图:主要研究一些简单的组合几何体的三视图还原,一般先从俯视图入手,再考虑主视图,最后考虑左视图。
四. 考点解析与典型例题
考点一 对几何体结构特征的认识
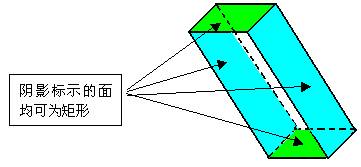
例1. 斜四棱柱的各个面中可能有矩形吗?如果有,最多可能有几个?
解:有可能;最多可能有四个。如图:
例2. 下述几何体是指定的几何体吗?为什么?
(1)四棱台:
(2)圆锥:
(3)圆台: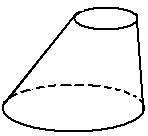
(4)棱柱: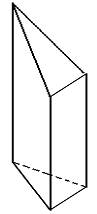
解:都不是。均不符合相应几何体的定义。
考点二 用斜二测画法画水平放置的平面图形的直观图。
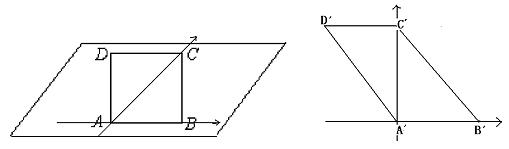
例3. 画出水平放置的正五边形ABCDE(如图)的直观图。
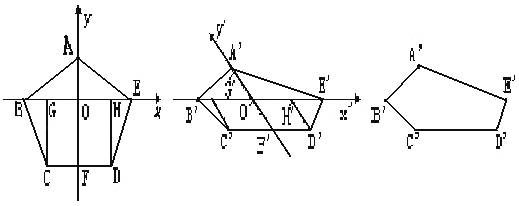
画法步骤:(1)在已知图形所在平面上建立平面直角坐标系xOy,另选一平面画直观图,先画x′轴和y′轴,使∠x′O′y′=45°或135°(如图)。
(2)将已知图形中平行于x轴或y轴的线段在直观图中分别画成平行于x′轴和y′轴的线段,且已知图形中平行于x轴的线段在直观图中保持原长度不变;平行于y轴的线段,在直观图中长度为原来的一半;
(3)连线成图(擦去辅助线)。
说明:画直观图的技巧主要是在x′O′y′中确定直观图的顶点的位置,所以要寻找或构造过定点且与x轴、y轴平行的线段。
例4. 已知一四边形ABCD水平放置的直观图是一个边长为2的正方形,请画出这个图形的真实图形。
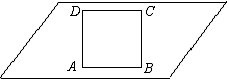
分析:关键是确定原图形的各个顶点。要充分利用斜二测画法规则中对平行性与长度变化的规定。
解:由斜二测画法规则可知,作图前后,AB=A′B′,CD=C′D′,A′C′=![]() 。
。
考点三 画一些简单的立体图形的直观图
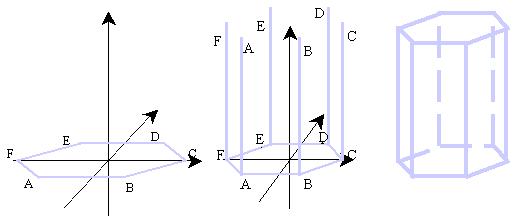
例5. 画底面水平放置的正六棱柱的直观图。
解:画法步骤:
(1)画底面(根据平面图形的直观图画法)
(2)画z'轴(z'轴与x'轴的交角为直角),并画高线(与原长相等),连线成图。
(3)擦去辅助线,被遮线画成虚线。
考点四 空间几何体的三视图
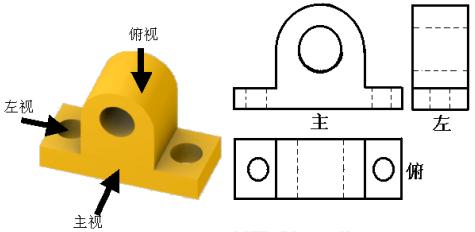
例6. 画出如图所示几何体的三视图。

解:画法步骤(1)确定主视图位置,画出主视图;
(2)画出俯视图(与主视图长对正);
(3)画左视图(与主视图高平齐,与俯视图宽相等)
例7. 已知一个几何体的三视图如图,试将其还原。
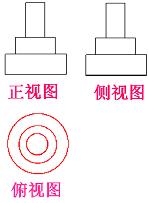
解:
五. 本讲涉及的主要数学思想方法
1、直观感知与抽象概括的能力和方法:我们生活在空间与图形的世界里,直观图形、几何模型以及几何图形的性质,是准确描述现实世界空间与图形关系,解决学习、生活与工作中各种问题的工具,随着计算机制图和成像技术的发展,处理空间与图形问题的几何方法被广泛运用到人类生活和社会发展的各个方面,因此,掌握空间与图形的能力是学生应具备的基本数学素养,对于我们更好地认识、理解生活的空间,更好地生存与发展具有重要意义。本讲涉及的简单几何体、直观图及三视图的有关知识就是我们进一步研究几何的基础,在培养直观感知和抽象概括能力方面具有基础性的意义。
2、直觉能力和空间想象能力:几何体作为一种直观、形象的数学模型,在发展学生的直觉能力,培养学生的空间想象能力和创新精神方面具有独特的价值,本讲对教学难点“通过三视图还原几何体”的突破,能有效地训练数学直觉能力和空间想象能力。
【模拟试题】(答题时间:30分钟)
一、选择题
1、下列命题正确的是( )
A. 直角三角形绕一边旋转得到的旋转体是圆锥;
B. 夹在圆柱的两个平行截面间的几何体还是一个旋转体;
C. 圆锥截去一个小圆锥后剩余部分是圆台;
D. 通过圆台侧面上一点,有无数条母线。
2、已知集合A={棱柱},B={正棱柱},C={斜棱柱},D={直棱柱},则( )
A. A![]() C
C![]() B B.
A
B B.
A![]() D
D![]() B C.
A
B C.
A![]() C
C![]() D D.
A
D D.
A![]() D
D![]() C
C
*3、给出下列四个命题:各侧面都是正方形的棱柱一定是正棱柱;‚对角面是全等矩形的平行六面体一定是长方体;ƒ有两个侧面垂直于底面的棱柱一定是直棱柱;④长方体一定是正四棱柱。其中正确命题的个数是( )
A. 0
B.
*4、利用斜二测画法得到:三角形的直观图是三角形;‚平行四边形的直观图是平行四边形;ƒ正方形的直观图是正方形;④菱形的直观图是菱形。以上结论正确的是( )
A. ①② B. ① C. ③④ D. ①②③④
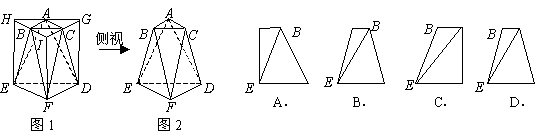
5、(2008广东卷)将正三棱柱截去三个角(如图1所示![]() 分别是
分别是![]() 三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )
三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )
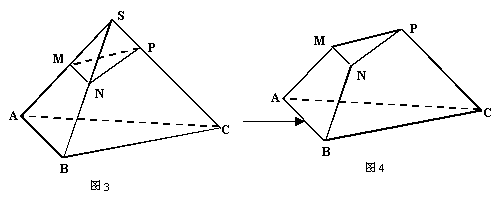
6、如图3示,S—ABC为正三棱锥,M、N为所在棱的中点,SP:PC=1:2,现由截面MNP将该三棱锥的顶部S-PMN截去,依图4方向画出它的左视图(侧视图),则正确的画法是( )
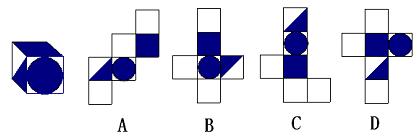
7、(2008上海)如图所示的立方体,如果把它展开,可以是下列图形中的( )
二、填空题
8、下面给出了三个命题,用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;‚两个底面平行且相似,其余各面都是梯形的多面体是棱台;ƒ有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台。其中正确命题的个数是
9、(2008山东卷6改)下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是 。

三、解答题
10、已知按照斜二测画法,水平放置的、边长为
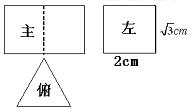
11、有一个正三棱柱的三视图如下,求其体积。
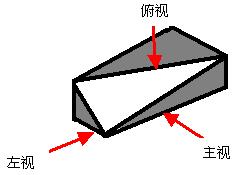
12、如图是一个截去一个角的长方体,试画出其三视图。
*13、已知地球的半径为R,球面上两点A、B都在北纬45°的圈上,它们的球面距离为![]() ,A点在东经30°,求B点的位置及A、B两点在其纬线圈上对应的劣弧的长度。
,A点在东经30°,求B点的位置及A、B两点在其纬线圈上对应的劣弧的长度。
【试题答案】
一、选择题:
1~7 CBB AAA D
二、填空题
8、0;
9、12π;
三、解答题
10、![]() ;
;
11、![]() ;
;
12、
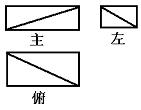
13、B点在东经120o或西经60o;劣弧长为![]() 。
。