![]()
课程解读
一、学习目标:
1. 能画出三角函数(正弦、余弦、正切)的函数图像。
2. 通过图像理解正弦函数、余弦函数、正切函数的性质。
3. 理解函数![]() 的图像性质及其图像的变换。
的图像性质及其图像的变换。
4. 能利用三角函数的图像解决简单的实际问题。
二、重点、难点:
重点:(1)掌握三角函数(y=sinx, y=cosx, y=tanx)的图像性质及其简单的应用。
(2)理解函数![]() 的图像及其性质。
的图像及其性质。
难点:三角函数图像的应用
三、考点分析:
从新课标高考命题的内容来看:对三角函数的图像与性质这部分知识点进行考查时的题型有选择、填空和中等难度的大题,都以考查基础知识为主。因此第一轮复习的重点是掌握三角函数的基础知识,并能灵活运用基础知识解决问题。
知识梳理
三角函数的图像与性质
知识要点解析:
一、三角函数的图像与性质:
|
函数 |
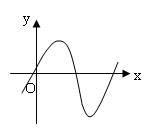
y=sinx |
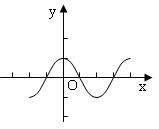
y=cosx |
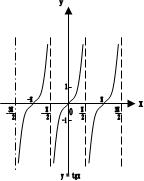
y=tanx |
|
图像 |
|
|
|
|
定义域 |
R |
R |
|
|
值域 |
[-1,1] |
[-1,1] |
R |
|
周期性 |
|
|
|
|
奇偶性 |
奇函数 |
偶函数 |
奇函数 |
|
单调性 |
增区间: [ 减区间:
|
增区间:
减区间:
|
在开区间:
上是增函数。 |
|
对称性 |
对称轴方程: 直线 对称中心坐标: |
对称轴方程: 直线 对称中心坐标:
|
对称中心坐标:
|
注意:(1)正弦、余弦函数的图像用“五点法”作图,选择(0,0),(![]() 这五个点可作出草图;
这五个点可作出草图;
(2)三角函数线的概念:
二、函数![]() 的图像与性质(
的图像与性质(![]()
1. 图像:利用“五点法”作函数![]() 的图像。令
的图像。令![]() ,然后列表、描点、连线。
,然后列表、描点、连线。
2. 性质:
(1)定义域:![]()
(2)值域:![]() ,(当
,(当![]() ;
;
当![]() )
)
(3)周期性:![]()
(4)奇偶性:![]() 是奇函数
是奇函数![]()
![]() 是偶函数
是偶函数![]()
(5)单调性:在区间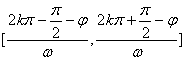 上递增,
上递增,
在区间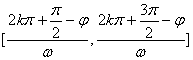 上递减。
上递减。
(6)对称性:对称轴方程:
三、函数![]() +k的图像变换
+k的图像变换
变换I:振幅变换![]() 周期变换
周期变换![]() 相位变换
相位变换
(1)y=sinx图像的横坐标不变,纵坐标伸长(A>1)或缩短(0<A<1)为原来的A倍得到y=Asinx的图像。
(2)y=Asinx图像的纵坐标不变,横坐标伸长(![]() )或缩短(
)或缩短(![]() )为原来的
)为原来的![]() 倍得到
倍得到![]() 的图像。
的图像。
![]() 的图像向左平移
的图像向左平移![]() 个单位得
个单位得![]() 的图像。
的图像。
![]() 个单位得到
个单位得到![]() 的图像。
的图像。
变换II:振幅变换![]() 相位变换
相位变换![]() 周期变换
周期变换
(1)y=sinx图像的横坐标不变,纵坐标伸长(A>1)或缩短(0<A<1)为原来的A倍得到y=Asinx的图像。
(2)![]() 的图像向左平移
的图像向左平移![]() 个单位得
个单位得![]() 的图像。
的图像。
(3)y=Asin(x+![]() )图像的纵坐标不变,横坐标伸长(
)图像的纵坐标不变,横坐标伸长(![]() )或缩短(
)或缩短(![]() )为原来的
)为原来的![]() 倍得到
倍得到![]() 的图像。
的图像。
(4)![]() 个单位得到
个单位得到![]() 的图像。
的图像。
注意上述两种变换的区别。
典型例题
知识点一:函数![]() 的图像与性质
的图像与性质
例1.
基础题
1. 函数y=![]() 的定义域是_____________。
的定义域是_____________。
2. 不等式![]() 的解集是____________。
的解集是____________。
3. 函数![]() 的递增区间是____________。
的递增区间是____________。
4. 函数![]() 的值域是____________。
的值域是____________。
思路分析:
1. 由![]() 结合三角函数线或余弦函数图像求x的取值范围。
结合三角函数线或余弦函数图像求x的取值范围。
2. 利用正、余弦函数图像或三角函数线求不等式的解集。
3. 根据正切函数y=tanx的递增区间求函数![]() 的递增区间。
的递增区间。
4. 用y表示sinx,再利用![]() 求y的取值范围。或用分离常数法求解。
求y的取值范围。或用分离常数法求解。
解题过程:
1. 由已知得:![]()
![]()
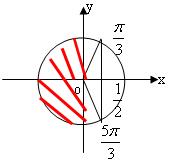
由三角函数线知:角x的取值范围是如图所示的阴影区域。
故函数的定义域是![]() 。
。
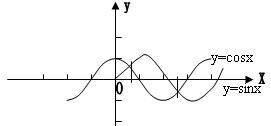
2. 在同一坐标系中画出函数y=sinx与y=cosx的图像。
由图知:使![]() 成立的x的取值范围(解集)是:
成立的x的取值范围(解集)是:
![]()
3. 设t=![]()
由函数![]() 的递增区间是
的递增区间是![]()
![]() ,
,
故![]()
即函数![]() 的递增区间是
的递增区间是![]()
4. 由已知得:![]() (
(![]() ,
,![]()
整理得:![]() ,即函数的值域是[-2,0]
,即函数的值域是[-2,0]
另解:![]() =
=![]() ,令
,令![]()
![]() ,显然y是t的减函数,故
,显然y是t的减函数,故![]() ,即函数的值域是[-2,0]
,即函数的值域是[-2,0]
用这种方法求解时要注意函数的定义域。
如求![]() 的值域,采用分离常数法时要注意:
的值域,采用分离常数法时要注意:
![]() ,此时
,此时![]() ,因
,因![]() ,故
,故![]() 。
。
若不考虑定义域会误认为:![]() 从而得出错误的结果。
从而得出错误的结果。
解题后的思考:利用基本三角函数的性质求函数的值域或求函数的单调区间或求令简单的三角不等式成立的x的取值范围等问题是高考常见题型,且几乎都是客观题。我们除要掌握基础知识外,还要掌握一些常用的数学思想方法。要做到触类旁通,如求![]() 的值域问题其实与本例第4题的做法一样。
的值域问题其实与本例第4题的做法一样。
例2.
中等题
1. 函数![]() 的最大值是______。
的最大值是______。
2. 函数![]() 的最大值是M,最小值是N,则M+N=_________________。
的最大值是M,最小值是N,则M+N=_________________。
3. 已知函数![]()
(1)求函数f(x)的最小正周期。
(2)求函数![]() 的最大值、单调区间、对称轴方程及取得最大值时x的取值集合。
的最大值、单调区间、对称轴方程及取得最大值时x的取值集合。
思路分析:
1. 利用正弦函数递增区间是![]() ,则可由
,则可由![]() 建立
建立![]() 的不等关系式。
的不等关系式。
2. 求函数![]() 的值域,可利用
的值域,可利用![]() 求解。
求解。
3. (1)化简f(x)的函数式,用正弦或余弦表示。再利用T=![]() 求出周期。
求出周期。
(2)先确定h(x)的函数解析式,然后再求其最值、单调区间、对称轴方程等。
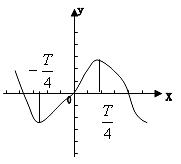
解题过程:1. 由于f(x)在区间![]() 上递增(如图)
上递增(如图)
![]()
![]()
2. 由![]() 得:
得:![]()
![]() (
(![]()
![]() ,两边平方
,两边平方
整理得:![]() ,
,
![]()
3. (1)由![]()
=![]()
故函数f(x)的最小正周期是![]()
(2)![]()
由![]()
由![]()
故函数h(x)的增区间是![]() ,
,
最大值是![]() ,此时对应的x的值是
,此时对应的x的值是![]()
故x的取值集合是![]() ,
,
对称轴方程:![]()
解题后的思考:对于求形如![]()
![]() 的值域问题,及求复杂函数的周期单调时区间、等问题常采用以下变换:
的值域问题,及求复杂函数的周期单调时区间、等问题常采用以下变换:![]() 。因此这个变换很重要,实质是正、余弦的和(差)角公式的应用。
。因此这个变换很重要,实质是正、余弦的和(差)角公式的应用。
例3. 创新与应用
已知向量![]()
(1)求函数![]() 及对称轴方程。
及对称轴方程。
(2)若函数![]() 为偶函数,求
为偶函数,求![]() 的值。
的值。
思路分析:(1)由向量的坐标运算,先确定f(x)的解析式,再确定值域和对称轴方程。
(2)由函数![]() 是偶函数
是偶函数![]() 及x的取值范围确定
及x的取值范围确定![]() 的值。
的值。
解题过程:(1)![]()
=![]()
故函数f(x)的值域是[-2,2],对称轴方程是![]()
即![]()
(2)![]()
![]()
又![]()
解题后的思考:三角函数与平面向量的结合一直是新课标高考命题的重要题型。以向量为载体具体考查三角函数的恒等变换及三角函数的图像与性质。我们应该关注这种题型。
知识点二:函数![]() 的图像与性质
的图像与性质
例4.
基础题
1. 函数y=sin2x的图像向左平移![]() 个单位,再向上平移1个单位所得函数的解析式是________。
个单位,再向上平移1个单位所得函数的解析式是________。
2. 已知函数![]() 的最小正周期是
的最小正周期是![]() ,将y=f(x)的图像向左平移
,将y=f(x)的图像向左平移![]() 个单位,所得图像关于原点成中心对称,则
个单位,所得图像关于原点成中心对称,则![]() =_______________。
=_______________。
3. 函数![]() 在[0,
在[0,![]() 上的单调递增区间是______________。
上的单调递增区间是______________。
思路分析:1. 函数y=sin2x向左平移![]() 个单位是:
个单位是:![]() 。
。
2. 由已知得![]() =2,故
=2,故![]() 由平移后的函数图像关于原点对称求|
由平移后的函数图像关于原点对称求|![]() |的值。
|的值。
3. 由正弦函数y=sinx的增区间得:![]() ,求出x的取值区间,再赋予k的整数值,从而求出符合条件的单调区间。
,求出x的取值区间,再赋予k的整数值,从而求出符合条件的单调区间。
解题过程:1. 函数y=sin2x向左平移![]() 个单位后得:
个单位后得:![]() ,再向上平移1个单位后得:
,再向上平移1个单位后得:![]()
![]()
2. 由已知得:![]() =2,故
=2,故![]() 向左平移
向左平移![]() 得:
得:![]() ,即
,即![]()
![]()
3. 由已知得:![]()
![]()
![]()
![]()
解题后的思考:对函数图像的平移不仅要注意平移的单位,更要注意平移的方向即:x轴方向上的平移是“左加右减”,y轴方向上的平移是“上加下减”,对函数y=![]() 的奇偶性的讨论应注意:y=
的奇偶性的讨论应注意:y=![]() 是奇函数的充要条件是:
是奇函数的充要条件是:![]()
例5.
中等题
1. 已知函数![]() >0,A>0,
>0,A>0,![]() 的图像如图,求函数f(x)的解析式。
的图像如图,求函数f(x)的解析式。
2. 已知函数![]() ;
;
(1)当x![]() 时,求函数的值域。
时,求函数的值域。
(2)求图像上距原点最近的对称中心坐标。
(3)若角![]() 的终边不共线,且
的终边不共线,且![]() 。
。
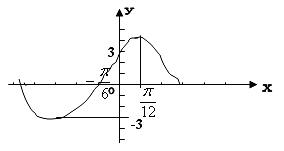
思路分析:1. 根据函数图像,求出A=3,![]() 的值,由当x=
的值,由当x=![]() 时,y=0得出
时,y=0得出![]() 的范围从而求
的范围从而求![]() 的值。
的值。
2. (1)化简函数式为![]() ,然后求其值域。
,然后求其值域。
(2)由![]() 确定图像上距原点最近的对称中心坐标。
确定图像上距原点最近的对称中心坐标。
(3)由角![]() 的终边不共线,且
的终边不共线,且![]() 的值。
的值。
解题过程:1. 由图像知:A=3,![]() ,又
,又![]()
![]() ,故函数
,故函数![]() 的解析式为
的解析式为![]() 。
。
2. (1)![]() ,当x
,当x![]() 时,
时,![]() ,
,![]()
(2)由![]()
![]()
![]() ,即图像上距原点最近的对称中心坐标是
,即图像上距原点最近的对称中心坐标是![]()
(3)由已知得:![]() 又
又![]() 不共线得:
不共线得:![]() ,
,![]()
解题后的思考:求解函数![]() 的解析式问题时,关键是确定
的解析式问题时,关键是确定![]()
![]() 这四个量
这四个量![]() ,根据函数的最值确定A,k的值,由函数的周期确定
,根据函数的最值确定A,k的值,由函数的周期确定![]() 的值,较难确定的是
的值,较难确定的是![]() 的值。根据“五点法”作图原理知:在一个周期内,图像上升时与x轴的第一个交点满足:
的值。根据“五点法”作图原理知:在一个周期内,图像上升时与x轴的第一个交点满足:![]() ;第二个点是图像的最高点,满足:
;第二个点是图像的最高点,满足:![]() ;第三个点是图像下降时与x轴的交点,满足:
;第三个点是图像下降时与x轴的交点,满足:![]()
![]() ;第四个点是图像的最低点,满足:
;第四个点是图像的最低点,满足:![]() ;第五个点满足:
;第五个点满足:![]() 。由此确定
。由此确定![]() 的值(同时注意已知条件中的
的值(同时注意已知条件中的![]() 的取值范围)。
的取值范围)。
例6.
实际应用
已知某海滨浴场的海浪的高度y米是时间t(0![]() (单位:时)的函数,记作:
(单位:时)的函数,记作:![]()
下表是某日各时浪高的数据:
|
t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y(米) |
1.5 |
1.0 |
1.5 |
1.0 |
1.5 |
1 |
0.5 |
0.99 |
1.5 |
经长期观测,y=f(t)的曲线可近似地看成函数y=![]()
(1)求函数y=![]() 的最小正周期T,振幅A及函数解析式。
的最小正周期T,振幅A及函数解析式。
(2)依据规定:当海浪的高度高于
思路分析:由表中的数据可以得出:周期T=12,从而求出![]() 的值,再由表中的数据建立A,b的关系式,则可求出函数解析式。由y>1求出时间t的取值范围,进而确定冲浪的时间。
的值,再由表中的数据建立A,b的关系式,则可求出函数解析式。由y>1求出时间t的取值范围,进而确定冲浪的时间。
解题过程:由表中的数据得:T=12,故![]() =
=![]() ,
,
由t=0时,y=1.5得:A+b=1.5, 由t=3时,y=1.0得:b=1.0,![]()
故函数解析式是![]()
由![]() ,
,
![]() ,令k=0,1,2得:
,令k=0,1,2得:
![]()
故一天内的上午8:00到晚上20:00之间,有6个小时的时间可供冲浪爱好者进行运动,即上午9:00到下午的15:00。
解题后的思考:本题考查三角函数的实际应用,解题关键是提炼和归纳已知(或图表)中的信息,从而锻炼自己处理数据信息的能力。
预习导学
一、预习新知
1. 三角形有几个元素?直角三角形的边与角的关系是什么?
2. 直角三角形的三条边分别是a,b,c,三个角分别是A,B,C,则结论:![]() 成立吗?这一结论能否推广到一般的三角形中去?
成立吗?这一结论能否推广到一般的三角形中去?
二、预习点拨:
(解三角形:已知三角形的边和角,求其余的边和角)
1. 直角三角形的边与角的关系是__________,__________,__________,
2. 正弦定理
(1)正弦定理的内容是:________________________________________。
(2)正弦定理的数学表达式是______________________________。
(3)正弦定理应用于解两种类型的三角形是指:
(i)_____________________________,(ii)______________________。
(4)在“已知三角形的两边和其中一边的对角”,利用正弦定理求其余的边和角这一题型中,解的情形有几种?
3. 余弦定理:
(1)余弦定理的内容是:__________。
(2)余弦定理的数学表达式是:__________,__________,__________。
余弦定理应用于解两种类型的三角形是指:(i)_________________________________。
(ii)___________________________________________________________________。
4. 解三角形的工具除了正、余弦定理外,还有哪些定理?
同步练习
(答题时间:45分钟)
一. 选择题
1. 函数y=![]() 的一条对称轴是( )
的一条对称轴是( )
![]()
2. 将函数![]() 图像上所有点的横坐标伸长为原来的2倍(纵坐标不变),再将图像向左平移
图像上所有点的横坐标伸长为原来的2倍(纵坐标不变),再将图像向左平移![]() 个单位,得到函数g(x)的图像,则g(x)=( )
个单位,得到函数g(x)的图像,则g(x)=( )
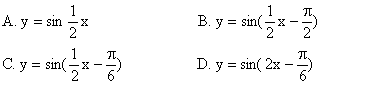
3. 函数![]() 中,周期都是
中,周期都是![]() 的有( )个。
的有( )个。
A. 1 B.
4. 函数![]() 是R上的偶函数,则
是R上的偶函数,则![]() ( )
( )
![]()
![]()
5. 函数![]() 的图像关于直线
的图像关于直线![]() 对称,则
对称,则![]() 的值可能是( )
的值可能是( )
![]()
*6. 函数y=sinx-|sinx|的值域是( )
A. [-1,0] B.
[0,1] C.
[-1,1] D.
[-2,0]
二. 填空题
*7. 函数![]() 的最大值是——————。
的最大值是——————。
8. 若函数![]() 的最小正周期为T,且1<T<2,则自然数k的值是______。
的最小正周期为T,且1<T<2,则自然数k的值是______。
*9. ![]() 在
在![]() 上的最大值是
上的最大值是![]() ,则
,则![]() 。
。
10. 函数![]() 的单调递减区间是_________________。
的单调递减区间是_________________。
三.
计算题
*11. 已知函数![]()
(1)若cos![]() 的值。
的值。
(2)在(1)的条件下,若函数f(x)的图像的相邻两条对称轴之间的距离是![]() ,求函数f(x)的解析式,并求最小正实数m使得函数f(x)的图像向左平移m个单位后所对应的函数是偶函数。
,求函数f(x)的解析式,并求最小正实数m使得函数f(x)的图像向左平移m个单位后所对应的函数是偶函数。
![]()
试题答案
一.
选择题
1. B解析:由![]() ,当k=1时,
,当k=1时,![]()
2. C解析:![]()
3. C解析:y=sin|x|不是周期函数,其余三个的周期都是![]() 。
。
4. C解析:由已知:![]()
5. B解析:由已知:![]() ,结合选项知选B
,结合选项知选B
6. D解析:![]()
![]()
二.
填空题
7. 3(解析:由![]()
![]() )
)
8. 2或3(解析:![]()
![]() )
)
9. ![]() (解析:由
(解析:由![]() ,即
,即![]()
10. ![]() ,
,![]()
(解析:由![]() 得:
得:![]()
![]() ),
),![]()
三. 计算题
11. 解:(1)由cos![]()
![]() 。
。
(2)由已知得:![]() ,
,
函数f(x)的图像向左平移m个单位后所对应的函数为:
![]()
由g(x)是偶函数![]()
∴最小正实数![]()