![]()
课程解读
一、学习目标:
1. 理解合力、分力、力的合成和分解。
2. 掌握平行四边形定则的含义和使用方法,会进行力的合成和分解。
3. 会进行受力分析,会用正交分解法求解力的平衡问题。
二、重点、难点:
重点:
1. 理解什么是等效替代法。
2. 熟练掌握平行四边形定则的应用。
3. 会根据力的效果对其进行分解并利用三角形关系求解分力或合力。
4. 会利用正交分解法求解力的平衡问题。
难点:
1.“平行四边形定则”的理解和应用。
2. 按照力的实际效果分解力。
3. 正交分解方法的应用。
三、考点分析:
本节内容是力学的基础内容,对本节课内容的考查常和物体的平衡,牛顿运动定律及运动结合起来综合出题,是高考考查的重点。
|
内容和要求 |
考点细目 |
出题方式 |
|
合力、分力、力的合成、力的分解,共点力 |
合力和分力的等效替代关系 |
选择题、计算题 |
|
平行四边形定则在力的合成和分解中的应用 |
||
|
正交分解法在力的合成与分解中的应用 |
||
|
分析方法 |
等效替代法,正交分解法,平行四边形定则,矢量三角形法 |
选择题、计算题 |
知识梳理
一、
1、合力与分力
(1)合力与分力的概念:一个力产生的效果跟几个力共同作用产生的效果相同,这个力就叫做那几个力的合力,而那几个力就叫做这个力的分力。
(2)合力与分力的关系:
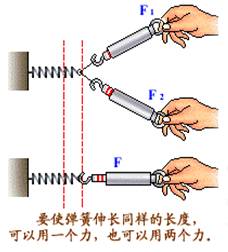
①合力与分力之间是一种等效替代的关系。一个物体同时受到几个力的作用时,如果用另一个力来代替这几个力而作用效果不变,这个力就叫那几个力的合力,但必须要明确合力是虚设的等效力,并非是真实存在的力。合力没有性质可言,也找不到施力物体,合力与它的几个分力可以等效替代,但不能共存,否则就添加了力。
②一个力可以有多个分力,即一个力的作用效果可以与多个力的作用效果相同。当然,多个力的作用效果也可以用一个力来代替。
2、共点力
(1)概念:几个力如果都作用在物体的同一点,或者它们的作用线相交于同一点,则这几个力叫共点力。
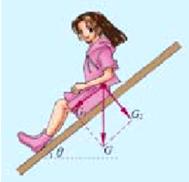
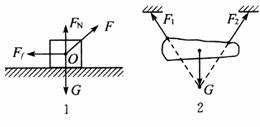
(2)一个具体的物体,所受的各个力的作用点并非完全在同一个点上,若这个物体的形状、大小对所研究的问题没有影响,我们就认为物体所受到的力就是共点力。如图甲所示,我们可以认为拉力F、摩擦力Ff及支持力FN都与重力G作用于同一点O。又如图乙所示,棒受到的力也是共点力。
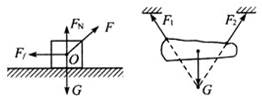
甲 乙
3、力的合成:
⑴概念:求几个力的合力叫力的合成。
⑵力的合成的本质:力的合成就是找一个力去代替几个已知的力,而不改变其作用效果。
⑶求合力的基本方法——利用平行四边形定则。
①平行四边形定则内容:如果用表示两个共点力F1和F2的线段为邻边作平行四边形,那么,合力F的大小和方向就可以用这两个邻边之间的对角线表示出来。这种方法叫做力的平行四边形定则。
注意:平行四边形定则只适用于共点力。
②利用平行四边形定则求解合力常用两种求解方法
Ⅰ. 图解法:从力的作用点起,按两个力的作用方向,用同一个标度作出两个力F1、F2,并构成一个平行四边形,这个平行四边形的对角线的长度按同样的比例表示合力的大小,对角线的方向就是合力的方向,用量角器直接量出合力F与某一个力(如F1)的夹角![]() ,如图所示。图中F1=40N,F2=50N,用直尺量出对角线长度,按比例得出合力F=80N,合力F与分力F1的夹角约为30°。
,如图所示。图中F1=40N,F2=50N,用直尺量出对角线长度,按比例得出合力F=80N,合力F与分力F1的夹角约为30°。
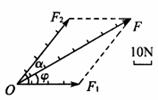
注意:使用图解法时,应先确定力的标度,在同一幅图上各个力都必须采用同一个标度,并且合力、分力的比例要适当,虚线、实线要分清。图解法的优点是简单、直观,缺点是不够精确。
Ⅱ. 计算法:找三角形利用边角关系求解
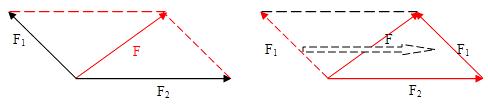
如下图所示,当两个力F1、F2互相垂直时,以两个分力F1、F2为邻边画出的力的平行四边形为一矩形,其合力F的大小为![]() 。
。
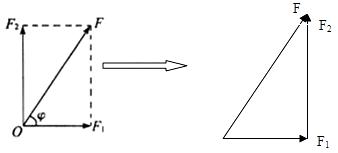
设合力与其中一个分力(如F1)的夹角为![]() ,由三角知识可得:
,由三角知识可得:![]() 。由此即可确定合力的方向。
。由此即可确定合力的方向。
◆分力的大小与合力的大小的关系
a. 两个分力同向,合力大小为两个分力之和。![]() ,方向不变。
,方向不变。
b. 两个分力反向,合力大小为两个分力之差。![]() ,方向与较大的力的方向相同。
,方向与较大的力的方向相同。
c. 两个分力间的夹角越大,合力的大小越小。
4、力的分解的概念
(1)分力:几个力共同作用产生的效果跟原来一个力作用产生的效果相同,这几个力就叫做原来那个力的分力。
(2)力的分解:求一个已知力的分力叫做力的分解。
注意:①力的分解就是找几个力来代替原来的一个力,而不改变其作用效果。合力与分力间是等效替代的关系。
②实际情况中如何根据力的作用效果进行分解。
5、力的分解的方法
(1)力的分解法则——力的平行四边形定则。
力的分解是力的合成的逆运算,同样遵守平行四边形定则。即把已知力作为平行四边形的对角线,那么与已知力共点的两条邻边就表示已知力的两个分力的大小和方向。
注意:一个力可以分解为无数多对分力。如图所示,要确定一个力的两个分力,一定要有定解的条件。
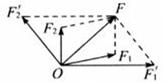
(2)对力分解时有解、无解的讨论
力分解时有解或无解,简单地说就是代表合力的对角线与给定的代表分力的有向线段是否能构成平行四边形(或三角形),如果能构成平行四边形(或三角形),说明该合力可以分解成给定的分力,即有解。如果不能构成平行四边形(或三角形),说明该合力不能按给定的分力分解,即无解。具体情况有以下几种:
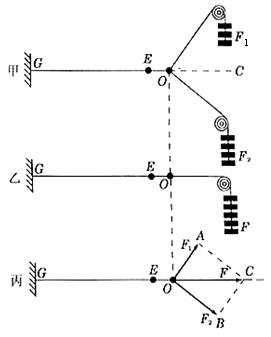
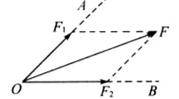
①已知两分力的方向(不在同一直线上)。如图所示,要求把已知力分解成沿OA、OB方向的两个分力,可以从F的箭头处开始作OA、OB的平行线,画出力的平行四边形,即可得两分力F1、F2。
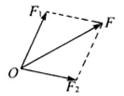
②已知一个分力的大小和方向。如图所示,已知一个分力为F1,则先连接合力F和分力F1的箭头,即为平行四边形的另一邻边,作出平行四边形,可得另一分力F2。
③已知两个分力的大小,有两解。
④已知一个分力的大小和另一个分力的方向,以表示合力F的线段末端为圆心,以表示![]() 的大小的线段长度为半径作圆。
的大小的线段长度为半径作圆。
Ⅰ. 当![]() 时,圆与F1无交点,此时无解,如图甲所示。
时,圆与F1无交点,此时无解,如图甲所示。
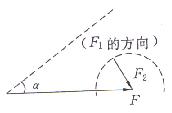
甲
Ⅱ. 当![]() 时,圆与
时,圆与![]() 相切,此时有一解,如图乙所示。
相切,此时有一解,如图乙所示。
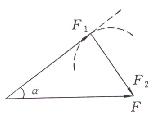
乙
Ⅲ. 当![]() 时,圆与
时,圆与![]() 有两交点,此时有两解,如图丙所示。
有两交点,此时有两解,如图丙所示。
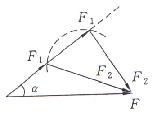
丙
Ⅳ. 当![]() 时,圆与
时,圆与![]() 只有一个交点,此时只有一解,如图丁所示。
只有一个交点,此时只有一解,如图丁所示。
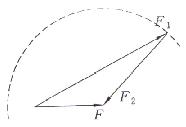
丁
(3)力的正交分解法
1)当物体受力较多时,我们常把物体受力沿互相垂直的两个方向分解,根据![]() =0,
=0,![]() =0 列方程求解。
=0 列方程求解。
把一个力分解成两个互相垂直的分力的方法叫做力的正交分解法。
基本思想:力的等效与替代
正交分解法是在平行四边形定则的基础上发展起来的,其目的是用代数运算解决矢量运算。
设已知力为F,现在要把它分解成两个分别沿x轴和y轴的分力。
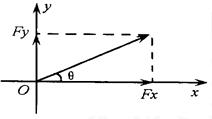
如图所示,将力F沿力x、y方向分解,可得:
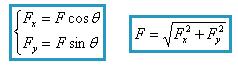
注意:①恰当地建立直角坐标系xOy,多数情况选共点力作用的交点为坐标原点,坐标轴方向的选择具有任意性,原则是:使坐标轴与尽量多的力重合,使需要分解的力尽量少和容易分解。
②将各力沿两坐标轴依次分解为互相垂直的两个分力。注意:与坐标轴正方向同向的分力取正值,与坐标轴负方向同向的分力取负值。
2)①平衡状态:使物体保持静止状态或匀速直线运动状态
②共点力作用下物体的平衡条件:物体受到的合外力为零。即F合=0
说明:①物体受到N个共点力作用而处于平衡状态时,取出其中的一个力,则这个力必与剩下的(N-1)个力的合力等大反向。
②若采用正交分解法求平衡问题,则其平衡条件为:Fx合=0,Fy合=0;
典型例题
知识点一:对合力、分力、共点力的理解
【例1】下列关于合力与分力的叙述,不正确的是( )
A. 一个物体受到几个力的作用,同时也受到这几个力的合力的作用
B. 几个力的合力总是大于它各个分力中最小的力
C. 合力和它相应的分力对物体的作用效果相同
D. 力的合成就是把几个力的作用效果用一个力来代替
正确答案:A、B
解答过程:几个力的合力与这几个力的作用效果是相同的,它们是可以相互替代的,合力与分力不能同时作用在物体上,所以A错误,C、D正确;而合力可以大于其中任一个分力,也可以小于任一个分力。所以B错误。
【例2】下面关于共点力的说法中正确的是( )
A. 物体受到的外力一定是共点力
B. 共点力一定是力的作用点在物体上的同一点上
C. 共点力可以是几个力的作用点在物体的同一点上,也可以是几个力的作用线交于同一点
D. 以上说法都不对
正确答案:C
解答过程:共点力的定义为:几个力如果都作用在物体上的同一点,或者它们的作用线相交于同一点,这几个力叫做共点力。所以C正确,A、B、D错误。
知识点二:力的合成与平行四边形定则的理解和应用
【例1】有两个共点力,F1=2N,F2=4N,它们的合力F的大小可能是( )
A. 1N B.
5N C.
7N D.
9N
命题目的:本题考查共点力的合成
正确答案:B
解答过程:两个共点力F1=2N、F2=4N,当力F1、F2方向相同时,合力最大,且Fmax=F1+F2=2N+4N=6N;当力F1、F2方向相反时,合力最小,且Fmin=4N-2N=2N。所以这两个力F1、F2的合力范围为[2N,4N],从上述四个选项中可看出,合力在此范围内的力只有B。
解题后思考:本题主要考查二力合成的平行四边形定则及二力合成的范围。要求知道二力合成时合力范围在两力大小之和与两力大小之差之间,即|F1-F2|<F<F1+F2,这样就可以选出正确的选项。
拓展1、大小分别是5 N、7
N、9 N的三个力的合力F的大小范围是( )
A. 2 N≤F≤20 N B.
3 N≤F≤21 N C. 0≤F≤20 N D. 0≤F≤21 N
正确答案:D
解答过程:这三个力方向相同时,合力最大,最大值为21 N;因为5
N和7 N的合力最大值是12 N,最小值是2 N,故5
N和7 N的合力可以是9 N,那么5 N、7
N、9 N这三个力合力的最小值可以是零,即0≤F≤21 N,D对。
解题后思考:三力合成最大时即三力方向相同,最小时可根据三个力的大小是否可构成三角形进行判断,若能,则最小合力为零。
【例2】如图所示,AB为半圆的一条直径,P点为圆周上的一点,在P点作用了三个共点力F1、F2、F3,求它们的合力。

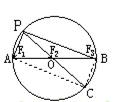
正确答案:
解答过程:如图所示,将半圆补画成完整的圆,延长PO交圆周于C点,连接AC、BC,易知:四边形PACB为平行四边形。所以,F1、F3的合力为
解题后思考:运用几何方法求多力合成问题,是多力合成问题中比较灵活的一类,解决此类问题的关键是找出题目几何特点,并能够将几何知识恰当地运用到力的合成中。
【例3】两位同学共同提一桶水,水和桶的总质量是
正确答案:84.9 N
解答过程:两位同学提力的合力等于水和水桶的重力,对水和水桶进行受力分析及求分力如下图所示,所以F=![]() =
=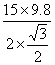 N=84.9 N。
N=84.9 N。
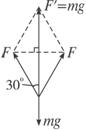
解题后思考:求解平行四边形时可先找出平行四边形中所包含的三角形的关系,再利用边角关系求解。
拓展2、如图,跳伞运动员打开伞后经过一段时间,将在空中保持匀速降落.已知运动员和他身上装备的总重力为G1,圆顶形降落伞伞面的重力为G2,伞面下有8条相同的拉线,一端与飞行员相连(拉线重力不计),另一端均匀分布在伞面边缘上(图中没有把拉线都画出来),每根拉线和竖直方向都成30°角。那么每根拉线上的张力大小为( )

A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
正确答案:A
解答过程:因为8条相同的拉线,均匀分布在伞面边缘上,过中心作一截面图,如图所示,由于拉线分布对称,每根绳上张力相同,对运动员进行受力分析可知:人受到重力G和8根拉线的拉力FT,由于跳伞运动员在空中保持匀速降落,由平衡知识可求出。
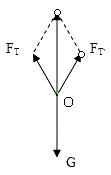
拉线拉力FT为:![]()
![]() ,故选项A正确。
,故选项A正确。
解题后思考:若弄不清楚本题的研究对象,把人和降落伞看作一个整体而求解拉线的拉力可能误选B或者C。错误原因是把人和降落伞看作一个整体时,拉线的拉力就成了系统的内力,本题应把拉线的拉力当作外力来处理,所以选项B、C错误;因拉线与竖直方向有30°夹角,根据人受到的平衡力,求出的结果不是![]() G,所以选项D错误。
G,所以选项D错误。
知识点三:力的分解
一个已知力的实际分力的确定方法
基本步骤:

【例1】如下图甲所示,电灯的重力G=10N,绳AO与顶板间夹角为45°,绳BO水平,则绳AO所受的拉力![]() __________;绳BO所受的拉力
__________;绳BO所受的拉力![]() __________。
__________。

甲
解析:将电灯拉O点的力分解在OA、OB上。
先分析物理现象:为什么绳AO、BO受到拉力呢?原因是由于绳OC的拉力产生了两个效果:一是沿AO向下的拉紧AO的分力![]() ;二是沿BO向右拉紧绳BO的分力
;二是沿BO向右拉紧绳BO的分力![]() ,画出平行四边形,如图乙所示,因为OC的拉力等于电灯重力,因此由几何关系得:
,画出平行四边形,如图乙所示,因为OC的拉力等于电灯重力,因此由几何关系得:
![]()
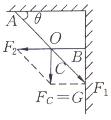
乙
答案:![]()
点拨:将一个已知力分解,在理论上是任意的,只要符合平行四边形定则就行,但在实际问题中,首先要弄清所分解的力有哪些作用效果,再确定各分力的方向,最后应用平行四边形定则解题。
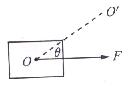
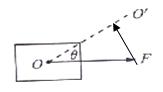
【例2】物体静止于光滑水平面上,力F作用于物体上的O点,现要使合力沿着OO′方向,如下图所示,则必须同时再加一个力F′,使F和F′均在同一水平面上,则这个力的最小值为( )。
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
正确答案:B
题意分析:此题考查力在分解过程中极值的情况。
解题过程:作出分力和合力的图示,得到平行四边形来求解。当F′与OO′垂直时分力最小。
【例3】一位同学在厨房里帮助妈妈做菜时对菜刀产生了兴趣,他发现菜刀的刀刃前部和后部的薄厚程度不一样,刀刃前部的顶角小,后部的顶角大(如下图),他先后作出过几个猜想,其中合理的是( )。

A. 刀刃前部和后部薄厚不匀,仅是为了打造方便,外形美观,跟使用功能无关
B. 在刀背上加上同样的压力时,分开其他物体的力跟刀刃薄厚无关
C. 在刀背上加上同样的压力时,顶角越大,分开其他物体的力越大
D. 在刀背上加上同样的压力时,顶角越小,分开其他物体的力越大
解析:把刀刃部分抽象后,可简化成一个等腰三角劈,设顶角为![]() ,背宽为d,侧面长为l,如下图(a)所示。
,背宽为d,侧面长为l,如下图(a)所示。
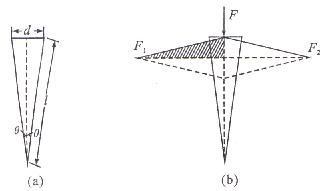
当在劈背施加压力F后,产生垂直于侧面的两个分力![]() ,使用中依靠这两个分力分开被加工的其他物体。由对称性知,这两个分力大小相等(
,使用中依靠这两个分力分开被加工的其他物体。由对称性知,这两个分力大小相等(![]() ),因此画出力分解的平行四边形,为菱形,如图(b)所示。
),因此画出力分解的平行四边形,为菱形,如图(b)所示。
在这个力的平行四边形示意图中,取其四分之一考虑(图中阴影部分)。根据它跟半个劈的直角三角形的相似关系,有关系式
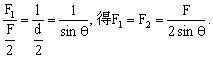
由此可见,刀背上加上一定的压力F时,侧面分开其他物体的力跟顶角的大小有关。顶角越小,![]() 的值越小,
的值越小,![]() 越大。
越大。
但是,刀刃的顶角越小时,刀刃的强度便会减小,若碰到较硬的物体时刀刃会卷口甚至碎裂。实际制造过程中为了适应加工不同物体的需要,所以将菜刀做成前部较薄,后部较厚。使用时,用前部切一些软的物品(如鱼、肉、蔬菜、水果等),用后部斩劈坚硬的骨头之类的物品。俗话说:“前切后劈”,指的就是这个意思。
由此可见,这位同学最后的一次猜想是合理的。
答案:D
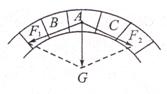
小结:生活中巧妙利用力的分解的例子还有很多。比如我国古代的能工巧匠利用合力与分力的道理,设计结构精美的拱桥,巧妙地将垂直向下的压力,转化为两个斜向下的分力(如下图),大大提高了桥梁的承载能力。这些桥早已在民间普及,人们用石头建造出大小、式样各异的拱桥,仔细观察,你会发现这些拱桥基本上与下图相似。
知识点四:正交分解法的应用
用正交分解法求多个力的合力的基本思路是:
1. 对研究对象进行受力分析。
2. 建立直角坐标系,再把不在轴上的所有的力沿两个坐标轴方向垂直分解。
3. 根据两个坐标轴方向列状态方程,解出未知量。
【例1】在水平路面上用绳子拉一个重力为G=200
N的木箱,绳子与水平路面的夹角θ=30°,如图所示.木箱与路面间的动摩擦因数μ=0.10,要使木箱能在水平路面上匀速移动,则绳上所加拉力F应为多大?
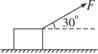
正确答案:21.8 N
解答过程:对物体进行受力分析,如图所示,木箱共受4个力的作用。将拉力F沿x轴和y轴分解得:F1=Fcosθ,F2=Fsinθ
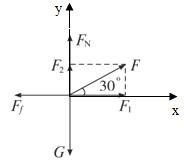
在y轴:F2+FN=G,FN=G-F2
在x轴:F1=Ff=μ(G-F2),即Fcosθ=μG-μFsinθ
F=![]() =
=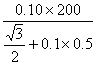 N=21.8 N。
N=21.8 N。
解题后思考:
不难看出,用正交分解法求合力的依据是合力与分力的等效替代关系,即将一个力分解后,利用它的两个分力求得的合力与直接利用这个力求合力的结果是相同的。
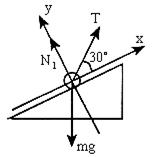
【例2】一个底面粗糙的质量为M的三角劈放在水平面上,三角劈的斜面光滑且与水平面成![]() 角。用一端固定的轻绳系一质量为m的小球,将小球放在斜面上,轻绳与竖直面的夹角为
角。用一端固定的轻绳系一质量为m的小球,将小球放在斜面上,轻绳与竖直面的夹角为![]() ,如下图所示。求当三角劈静止时绳子的张力T是多少?若地面对三角劈的最大静摩擦力等于地面对三角劈的支持力的k倍,为使整个系统静止,k值不能小于多少?
,如下图所示。求当三角劈静止时绳子的张力T是多少?若地面对三角劈的最大静摩擦力等于地面对三角劈的支持力的k倍,为使整个系统静止,k值不能小于多少?
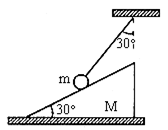
解答过程:以小球为研究对象,沿平行于斜面和垂直于斜面方向建立坐标系,其受力情况如下图所示。对T和mg进行正交分解,由物体的平衡条件有
![]()
所以![]()
再以三角劈和小球整体作为研究对象,沿水平方向和竖直方向建立坐标系,则整体受力情况如下图所示。将T正交分解后,对地面与三角劈间的最大静摩擦力fmax,由物体的平衡条件有![]()

且![]()
所以解得![]()
解题后思考:遇到斜面平衡问题时,一般沿斜面方向和垂直斜面方向建立坐标轴,在求解外力时可利用整体法分析。
提分技巧
1. 以两个分力为一组邻边,只能画出一个平行四边形,所以,根据两个分力只能求出一个合力。而仅根据一条对角线可以作出无数个平行四边形,有无数对不同的斜边,若没有其他条件限制,可以把一个力分解成无数组大小、方向不同的分力。
2. 在合力一定的情况下。随着两等大的分力间的夹角的增大,两分力增大,随着两分力间夹角的减小,两分力也减小。
3. 重力的分力仍是由于地球的吸引而产生的,且作用在物体上,其效果是使物体压紧斜面;而物体对斜面的压力是弹力,是由于物体形变产生的,其受力物体是斜面,所以重力沿垂直于斜面的分力与物体对斜面的压力是两个不同的力。
4. 因为力的合成与力的分解都是矢量运算,所以都遵守相同的法则,且它们互为逆运算。解决三个以上力的合成和分解常用正交分解法。
预习导学
一、预习新知
必修1 第三章 相互作用力复习
二、预习点拨
1. 总结常见的三种力,重力、弹力、摩擦力的产生条件及三要素。
2. 总结本章所涉及的解题方法。如,平行四边形定则,正交分解法等。
同步练习
(答题时间:45分钟)
1. 下列关于几个力与其合力的说法正确的是( )
A. 合力的作用效果跟原来那几个力共同作用的效果相同
B. 合力与原来那几个力同时作用在物体上
C. 合力的作用可以代替那几个力的作用
D. 求几个力的合力遵循平行四边形定则
2. 如图所示,是两个共点力的合力F跟它的两个分力之间的夹角θ的关系图象,则这两个力的大小分别是( )
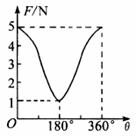
A. 1N和4N
B. 2N和3N C.
1N和5N D. 2N和4N
3. 有两个大小相等的共点力F1和F2,当它们的夹角为90°时,合力为F,则当它们之间的夹角为60°时,合力的大小为( )
A. ![]() C.
C.
![]() D.
D.
![]()
4. 有两个共点力F1和F2,其合力为F,则下列说法正确的是( )
A. 合力一定大于任一分力
B. 合力有可能小于某一分力
C. 分力F1增大,而分力F2不变,且它们的夹角不变时,合力F一定增大
D. 当两分力的大小不变时,增大两分力间的夹角,合力一定减小
5. 将已知力F分解为F1、F2两个分力,如果已知F1的大小及F2与F的夹角θ,且θ<90°,则下列说法正确的是( )
A. 当F1<Fsinθ时,F2一定有两个解
B. 当F>F1>Fsinθ时,F2一定有两个解
C. 当F1<Fsinθ时,F2有唯一解
D. 当F1<Fsinθ时,F2无解
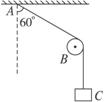
6. 如图所示,轻绳绕过一光滑的小圆柱B,上端固定于A点,下端系一重为200 N的物体C,AB段绳子与竖直方向的夹角为60°,则绳中张力大小为____________N,小圆柱B受到的压力大小为____________ N。
7. 在“验证力的平行四边形定则”的实验中,需要将橡皮条的一端固定在水平木板上,另一端系上两根细绳,如图所示.实验中需要两个弹簧秤分别钩住绳套,并互成角度地拉橡皮条。某同学认为此过程中必须注意以下几点:
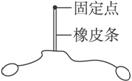
A. 两细绳必须等长
B. 橡皮条应与两绳夹角的角平分线在同一直线上
C. 在使用弹簧秤时要注意弹簧秤与木板平行
其中正确的是_____________。(填相应的字母)
8. 物体受几个共点力作用而保持静止状态,现将其中的一个力F1=3N转过90°,其他力保持不变,则物体所受的合外力为__________N,方向与原F1方向之间的夹角为__________。
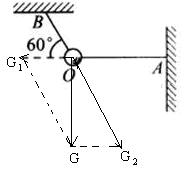
9. 如图所示,一只球用绳OA和OB拉住,OA水平,OB与水平方向成60°角,这时绳OB所受的拉力为8N,求小球的重力及绳OA的拉力的大小。

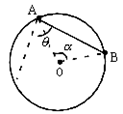
10. 如下图所示,两个重分别为GA和GB的小环A和B,用细线连着,套在一个竖直固定着的大圆环上。如果平衡时连线对圆心的张角为α,并当小圆环和大圆环之间的摩擦力以及线的质量都略去不计时,求连线与竖直方向的夹角θ。
![]()
试题答案
1. ACD 提示:根据对合力和分力关系的正确理解知,A、C、D对,B错。
2. B
提示:由图象可知:两个共点力夹角为0°或360°时方向相同,F合=F1+F2=5N;当两个共点力夹角为180°时,F合=|F1-F2|=1N,解得F1=2N,F2=3N或F1=3N,F2=2N.
所以B正确,A、C、D错误.
3. B 提示:作出两次的平行四边形,列方程求解。
4. BD
提示:合力和两个分力的关系,满足平行四边形定则,根据平行四边形定则可知,对角线可以大于任一边长,也可以小于某一边长或小于两个边长,故A错、B正确,同理可知D正确.当两个分力的夹角为锐角时,分力F1增大,而F2不变,且它们的夹角不变时,合力F一定增大;当两个分力方向相反时,分力F1增大,而F2不变,其合力可能增大,也可能减小,所以C错误。
5. BD
提示:若力F和它的两个分力F1、F2能构成平行四边形时,F1有最小值,最小值为F1=Fsinθ。当F1<Fsinθ时,无法构成平行四边形,则F2无解。当F>F1>Fsinθ时,能构成两个平行四边形,故F2有两个解,故B、D正确。
6. 200 200
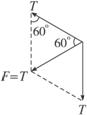
提示:因为轻绳下端静止悬挂着200 N的重物,所以绳的张力大小为200 N,小圆柱B受到的压力等于AB、BC两段绳子的拉力的合力,由图知合力的大小等于200 N。
7. C 提示:在“验证力的平行四边形定则”的实验中,弹簧秤的两个拉力必须与木板平面平行,以保证弹簧秤的拉力与橡皮条的拉力共面,从而减小误差,A、B两项是不必要的,只有C项正确。
8. ![]() ;135° 提示:设想撤去F1,再在与原F1垂直的方向上加上F1
;135° 提示:设想撤去F1,再在与原F1垂直的方向上加上F1
9. 小球的重力产生了两个效果,在这个力的作用下OA、OB两绳绷紧,沿AO、BO两方向拉绳,因此需要把G沿AO、BO两方向分解为G1、G2两分力。
如图所示,由二力平衡条件,得G2=FOB=8N,G2=G/sin60°=8N,
所以G=G2sin60°=8×![]() 。
。
FOA=G1=G2cos60°=8×![]() =4N。
=4N。
提示:本题应按力的作用效果进行分解,再利用直角三角形知识解题。
10. 对A环和B环受力分析如下图所示。分别以两小圆环所在处为坐标原点,沿该处的切线方向和法线方向(半径方向)建立各自的坐标系,其中半径OA、OB与连线的夹角![]() 。
。
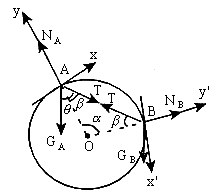
对A列出x轴方向的平衡方程
![]()
对B列出x轴方向的平衡方程
![]()
由以上两式可得
![]()
![]()
提示:遇到圆形或弧形上物体平衡的问题时,一般沿切线和与之垂直的半径方向建立坐标轴并列方程求解。