![]()
【本讲教育信息】
一、教学内容
视图,太阳光与影子
二、教学目标
1、经历探索基本几何体与其三视图之间的关系;
2、能根据三视图描述基本几何体或实物图形,培养和发展学生的推理能力和空间观念;
3、经历实践、探索的过程,了解平行投影的含义,并理解物体、影子、光线这三者之间的关系,能正确作图;
4、通过学生的自主探索与合作交流,发现不同时刻物体在太阳光下形成的影子的大小和方向的变化规律,并能根据物体影子的大小和方向确定时刻的先后顺序;
5、结合具体实例,初步体会视图在现实生活中的应用,感受数学与现实生活的密切联系,增强学生的数学应用意识.
三、知识要点

1、三视图的概念
视图——视,就是看的意思。将人的视线规定为平行投影线,然后正对着物体看过去,将所见物体的轮廓画出来的图形。
主视图就是从物体的前方看到的图,左视图就是从物体的左面所看到的图,俯视图就是从物体的上面看到的图。
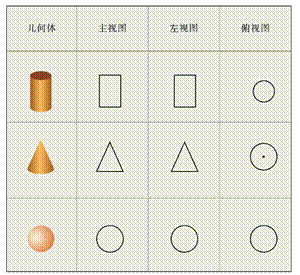

2、根据三棱柱、四棱柱画出物体的三视图
(在画视图时,看得见部分的轮廓线要画成实线,看不见部分的轮廓线要画成虚线)


3、投影:物体在光线的照射下,会在地面或墙壁上留下它的影子,这就是投影现象。
太阳光线可以看成平行光线,像这样的光线所形成的投影称为平行投影
(在北半球:一天中影子的变化方向为“西—西偏北—北—北偏东—东”,影子的长度变化为上午:“长—短”;下午“短—长”;一天变化为“长—短—长”。)

(可以利用相似图形的性质,得出“同一时刻,物高与影长成比例”这一结论来解题。)

四、重点难点
重点:1、圆柱、圆锥、球、直三棱柱和直四棱柱的三种视图的画法
2、太阳光线与影子的形成、平行投影的概念及平行投影和三视图的关系。
难点:1、从实物中抽象出几何体并能画出几何体的三种视图。
2、平行投影的概念及平行投影和三种视图的关系。
【典型例题】
考点一:主视图、左视图、俯视图的概念
例1、如图所示的图形是由7个完全相同的小立方体组成的立体图形,这个立体图形的主视图为( )
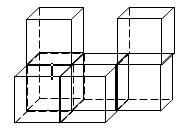
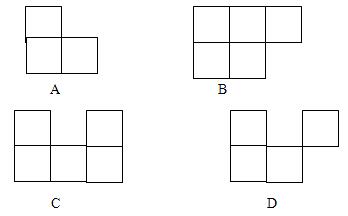
分析:主视图:从正面看到的图形;俯视图:从上面看到的图形;左视图:从左边看到的图形。图中所给四个选项中,A是左视图,B是俯视图,D是干扰图,只有C是主视图。故本题选C
考点二:根据三视图确定物体
例2、某物体的三视图如图所示,则该几何体可能是( )
A. 圆锥体 B. 球体 C. 长方体 D. 圆柱体

分析:俯视图是圆形,可以确定这个几何体是圆柱或球,又主视图和左视图都是长方形,所以可以确定这个几何体只能是圆柱。选D
考点三:三视图和组合物
例3、如图:是由若干个小立方块搭成的一个几何体的三视图,那么这个几何体中小正方块共有
个
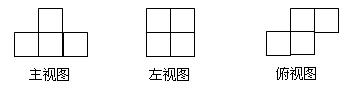
分析:从主视图来看,从左往右数的第二列有2个小正方形(说明上下有两层),因此俯视图中第二列的2个正方形中至少有一个要填2。(如下图,可有三种填法)
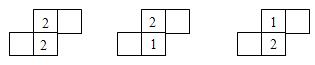
从主视图的第一列、第三列来看(都只有一个小正方形),俯视图的第一列、第三列均只能填1。(相应的也有三种情况)
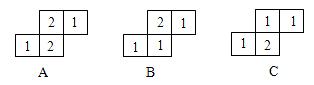
再从左视图来看,左边第一列、第二列均有两个小正方形,因此俯视图中后面即两行小正方形均要填2,于是只剩下上图A一种情形了,可见这个几何体由6个小正方块组成。
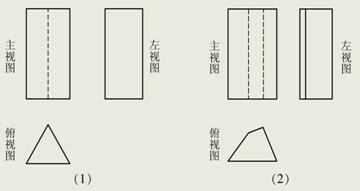
例4、如图A是一个几何体的主视图和左视图。某班同学在探究它的俯视图时,画出了如图B的几个图形,其中,可能是该几何体俯视图的共有( )个
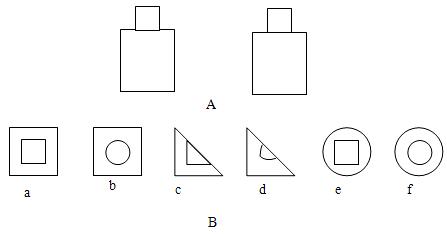
分析:由于题中的几何体由两部分组成,因此从图B的主视图和左视图,可以猜想几何体的形状由圆柱、三棱柱、正方体三种图形组合而成,这样上、下两部分的几何体的组合方案有几种,如下表:
|
上部 |
圆柱 |
圆柱 |
圆柱 |
正方体 |
正方体 |
正方体 |
三棱柱 |
三棱柱 |
三棱柱 |
|
下部 |
圆柱 |
正方体 |
三棱柱 |
正方体 |
圆柱 |
三棱柱 |
三棱柱 |
圆柱 |
正方体 |
|
俯视图 |
f |
b |
|
a |
e |
|
c |
|
|
考点四:平行投影
例5、如图中的三幅图是某同学在某地某天上午不同时间的同一位置观察到的。请通过观察,说出该同学观察的时间顺序,并说明理由。

分析:太阳东升西落,在早晨太阳位于正东方向,树的影子较长,且影子在树的正西方向,在上午,随着太阳位置的变化,影子的长度逐渐缩短,由此生活经验,不难判断出该同学观察的顺序。
解:顺序(3)(2)(1)。理由:太阳东升西落,在早晨位于正东方,此时树的影子较长,且影子位于树的正西方,在上午,随着太阳位置的变化,影子的长度逐渐缩短,影子长的是先观察到的,影子短的是后观察到的。
考点五:平行投影的性质
例6、在一次数学活动课上,
(1)请你在图中画出此时教学楼在阳光下的投影DF;
(2)请你根据已测得的数据,求出教学楼的高度(精确到
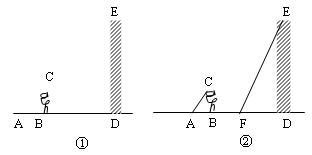
分析:(1)影子的确定我们可以根据平行投影光线平行的特点来确定。
(2)生活中,我们常利用“在同一时刻,不同物体的物高与影长成正比”测量高大物体的高度。(![]() )
)
解:(1)影子的长度如图②所示;
(2)由在同一时刻,不同物体的高度与影长成正比例,得:
![]() ,
,
解得DE=18.15≈18.2(米)
答:教学楼约高为
【方法总结】
教学中将重点放在怎样根据“研究问题的需要、三视图本身的特点”科学合理地选择实物,让学生通过亲自体验去感受三视图的内在变化与联系,太阳光与影子之间的关系,在实际生活中的应用、体现,体会数学的实际价值。
【预习导学方案】
第四章 第3节 灯光与影子,本章知识的回顾
(一)预习前知
1、中心投影
2、视点、视线、盲区
(二)预习导学
探索任务1:
确定下图中路灯灯泡所在的位置。
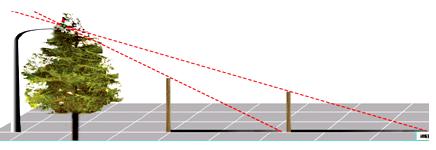
反思:如何确定光源的位置
探索任务2:
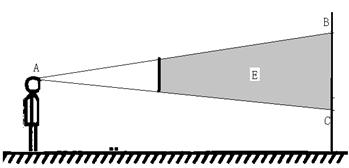
反思什么是视点、视线、盲区
探索任务3:
动手实践 升华认识
(1)两棵小树在同一时刻的影子如下图。请在图中画出形成树影的光线。它们是太阳的光线还是灯光的光线?与同伴进行交流。
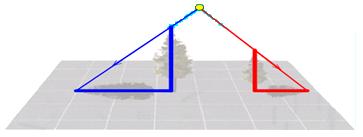
(2)下图的影子是在太阳光下形成的还是在灯光下形成的?画出同一时刻旗杆的影子,并与同伴交流这样做的理由。
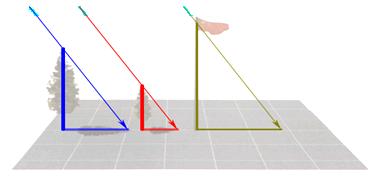
反思:比较灯光与太阳光所形成的影子的特点。
【模拟试题】(答题时间:30分钟)
一、填空题
1、平行投影是由 光线形成的。
2、一个正四棱柱的俯视图是
。
3、在我国北方某地上午9点和11点,同一棵树的影子 点时树影较长。
*4、某一时刻某木杆高
米。
二、选择题
1、一个几何体的主视图和左视图都是相同的长方形,俯视图为圆,则这个几何体为( )
A. 圆柱 B. 圆锥 C. 圆台 D. 球
*2、下列命题正确的是
A. 球的三视图均是半径相等的圆
B. 小华观察牡丹花,牡丹花就是视点
C. 三视图是中心投影
D. 阳光从矩形窗子里照射到地面上得到的光区仍是矩形
*3、在一个晴朗的天气里,小颖在向正北方向走路时,发现自己的身影向左偏,你知道小颖当时所处的时间是( )。
A. 上午 B.
中午 C. 下午 D.
无法确定
4、小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵随太阳转动的情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为( )。
A. 上午12时 B.
上午10时
C. 上午9时30分 D.
上午8时
5、对同一建筑物,相同时刻在太阳光下的影子冬天比夏天( )。
A. 短 B.
长 C. 看具体时间 D.
无法比较
*6、如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是( )。

A. ①②③④ B.
④①③② C. ④②③① D.
④③②①
7、太阳光照射一扇矩形的窗户,投在平行于窗户的墙上的影子的形状是( )。
A. 与窗户全等的矩形 B.
平行四边形
C. 比窗户略小的矩形
D.
比窗户略大的矩形
*8、在太阳光下,转动一个正方体,观察正方体在地上投下的影子,那么这个影子最多可能是几边形( )。
A. 四边形 B.
五边形 C.
六边形 D.
七边形
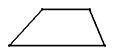
三、已知下图是一几何体的俯视图,请画出它的主视图和左视图
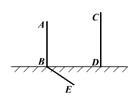
四、有两根木棒AB、CD在同一平面上直立着,其中AB这根木棒在太阳光下的影子BE如图所示,请你在图中画出这时木棒CD的影子.
五、在同一时刻,身高
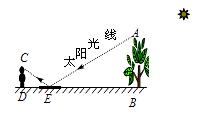
**六、为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:
根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如下示意图的测量方案:把镜子放在离树(AB)
![]()
【试题答案】
一、1、平行;2、正方形;3、9;4、1.2
二、1、A;2、A;3、A;4、D;5、B;6、B;7、A;8、C。
三、
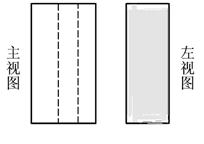
四、略。
五、
六、由题意知 ∠CED=∠AEB,∠CDE=∠ABE=Rt∠,
∴△CED∽△AEB ∴![]() ∴
∴![]() ∴AB≈
∴AB≈