![]()
【本讲教育信息】
一. 教学内容:
图形操作、视图
【教学目标】
1. 通过操作变换七巧板,培养学生的创造力和想像力。
2. 掌握一种新的数学思想方法——割补法。
3. 学会平铺地面及简单的计算与图案的设计。
4. 会判断简单几何体的三视图,并由三视图想像出几何体的实物模型,培养识图能力与观察能力。
二. 重点、难点:
1. 重点:
七巧板的制作、拼摆,画简单的空间图形的三视图。
2. 难点:
七巧板的灵活拼摆,画由简单图形组成的物体的三视图。
【知识要点】
1. 图形的分割与拼接,得到各式各样的几何图形,生产和生活中常用图形分割与拼接组成各种各样的器械和用具,数学中也常常用图形割补来方便于图形的计算。
2. 平面图形可以围成空间图形,空间图形也可以展开成平面图形。
3. 观察物体,从正面、上面、侧面(左侧面或右侧面)三个不同方向看一个物体,描绘出三个方向看到的形状,得出三个图。我们把这三个图分别叫正视图、俯视图、侧视图(左视图或右视图),这三个图合在一起称物体的三视图。
4. 三视图不是物体的真实形状,但由物体的三视图可以想像出物体的真实形状。
【典型例题】
例1. 自制七巧板,将七巧板拼成一条金鱼,再拼成一只帆船或一个矩形。
解:①自制七巧板,如下图(1)那样,把正方形厚纸板分成七部分,再割开。
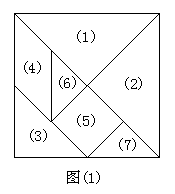
②将七巧板拼成一条金鱼如图(2)。
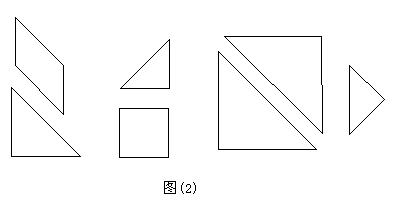
将七巧板拼成一只帆船如图(3)。
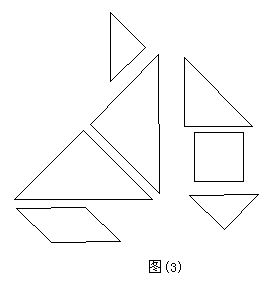
将七巧板拼成一个矩形如图(4)。
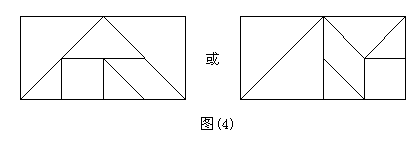
注意:用七巧板拼摆实物图形,关键要熟悉七巧板的各部分组成及关系和有丰富的想像力。
例2. 如图所示正方形边长为1
①分别计算阴影部分的面积。
②想一想,可得到怎样的结论。
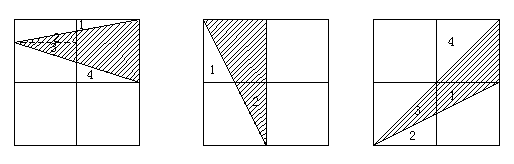
分析:![]()
算,也可以用割补法,如第一个(左起)图可把三角形(2)补到三角形(1)上,三角![]()
左起第二个图三角形(2)补到三角形(1)上。
左起第三个图三角形(1)补到三角形(2)上,三角形(2)与(3)补到三角形![]()
![]()
方形的一边长为三角形的高。
等底等高的三角形面积相等。
解:![]()
②等底等高的三角形面积相等。
例3. 设计一种用不同的正多边形地面砖平铺地面的图案。
分析:用不同的正多边形地面砖平铺地面必须使整数个(正整数)不同的正多边形的内角和为360°,即这些正多边形的一个顶点发出的若干个内角和为360°,这样平铺才不留缝隙,设计的方案有多种答案,如正方形与正三角形,正方形与正六边形、正三角形,正六边形与正三角形,正八边形与正方形等。
解:如图一种方案,用正方形与正三角形拼铺地面如下:
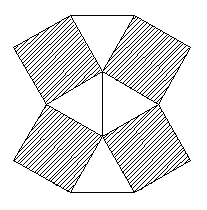
注意:不同的多边形的边长相等。
例4. ①观察图(a)中的几何体,指出图中的(1)、(2)、(3)分别是从哪个方向看几何体所得到的视图。
②观察图(b)中的三视图,说出该物体的名称。
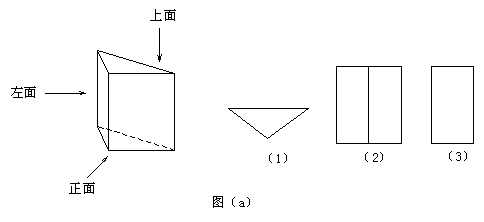
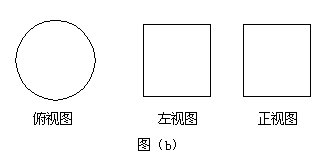
分析:此例中(1)问涉及由几何体得三视图的知识。
(2)问涉及由三视图得几何体知识点。
解:①图(a)中(1)为从上往下看得到俯视图。
(2)为从正面看得到的正视图。
(3)为从左往右看得到的左视图。
②由(b)图可看出这三个视图为圆柱体的视图,这个物体为圆柱体。
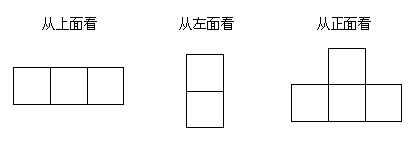
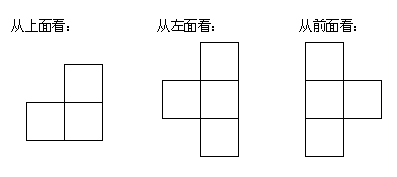
例5. 一个物体的三视图如图所示,请描述该物体的形状。
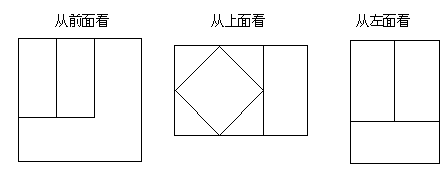
分析:由三个视图的主要轮廓,可以推测这个物体是以长方体为基础进行分割得到的,![]()
部分,由俯视图可推测在长方体的左上部截去了一个正方体的四个角,留下的是一个四棱柱,再结合左视图,这个四棱柱的三条棱分别经过原来长方体三条棱的中点。
解:物体的形状如下图所示:
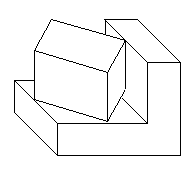
例6. 如下图一个几何体(由五个小正方体搭成的),画出它的三视图。
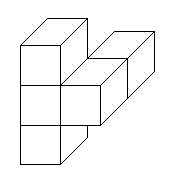
分析:这个图形由五个正方体构成,正方体的三视图都是正方形,所以三视图是由一些正方形构成。
解:物体的三视图如下所示:
【模拟试题】(答题时间:30分钟)
一. 填空题。
1. 观察物体,从正面、上面、侧面(左侧面或右侧面)三个不同方向看一个物体描绘出三个方向看到的形状,得到三个图,我们把这三个图分别叫做____________、___________、____________,它们合起来称为____________。
2. 用不同的多边形平铺地面,不留空隙,要求从一个顶点发出的多边形的内角和为____________,且这些多边形的边长要____________。
3. 在长方体、圆柱、棱锥、圆锥这些几何体的三视图中,绝对不可能有长方形的是____________。
4. 圆台的三视图是一个____________和两个____________。
二. 解答题。
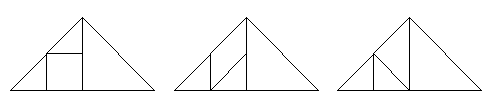
1. 用七巧板中的任四个部件拼出一个大直角三角形来。
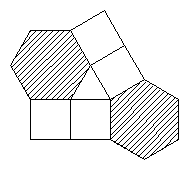
2. 用正六边形和正方形、正三角形平铺地面,设计一种图案。
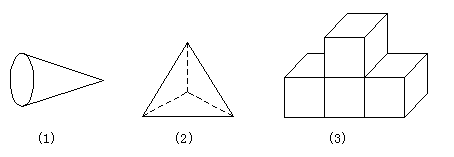
3. 画出下列物体的三视图。
![]()
【试题答案】
一. 填空题。
1. 正视图 俯视图 侧视图 三视图
2. 360° 相等
3. 圆锥
4. 有两个圆的同心圆 梯形
二. 解答题。
1. 如三种情况都可(答案多样)
2.
3. 解:(1)的三视图为:

(2)的三视图为:

(3)的三视图为: