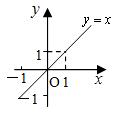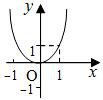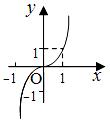课程解读

一、学习目标：

1. 掌握幂函数的概念。

2. 熟悉时幂函数的图象和性质。

3. 能利用幂函数的性质来解决一些实际问题。

二、重点、难点：

重点：幂函数的图象特点

难点：幂函数的性质及应用

三、考点分析：

这部分内容在高考中往往以基础知识为主，考查幂函数的图象和性质，一般以小题形式出现，属容易题。

知识梳理

1. 幂函数的定义

一般地，函数叫做幂函数，其中是自变量，是常数。

注意：

（1）幂函数中的指数a为任意实数。而指数函数中的底数a为大于0且不等于1的常数。

（2）只有形如的函数才叫做幂函数。

2. 幂函数的图象与性质

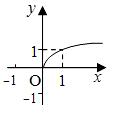
（1）幂函数的图象

名称	图象	定义域	值域	奇偶性	单调性
		R	R	奇函数	（－∞，＋∞）↑
		R	[0，＋∞）	偶函数	（－∞，0）↓ （0，＋∞）↑
		R	R	奇函数	（－∞，＋∞）↑
		[0，＋∞）	[0，＋∞）	非奇非偶函数	[0，＋∞）↑
		（－∞，0）∪ （0，＋∞）	（－∞，0）∪ （0，＋∞）	奇函数	（－∞，0）↓ （0，＋∞）↓

（2）幂函数的性质

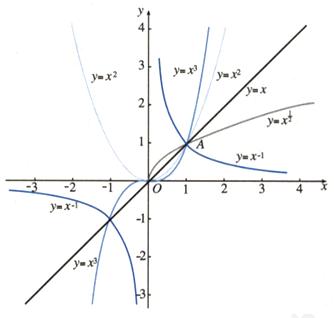
（1）所有的幂函数在（0，＋∞）上都有定义，并且图象都通过点（1，1）；

（2）如果α＞０，则幂函数的图象通过（0，0），并且在区间[0，＋∞）上是增函数；

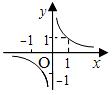
（3）如果α＜０，则幂函数在区间（0，＋∞）上是减函数，在第一象限内，当x从右边趋向于原点时，图象在y轴右方无限地逼近y轴，当x趋于＋∞时，图象在x轴上方无限逼近x轴。

典型例题

知识点一：幂函数比较大小

一、直接法

例1：比较下列各组中两个值的大小：

（1）；

（2），。

【思路分析】

题意分析：题中两组值都是幂运算的结果，且指数相同，因此可以利用幂函数的性质来判断它们的大小.

解题过程：（1）∵幂函数在（０，＋∞）上为增函数，又0.7＞0.6，

∴；

（2）∵幂函数在（０，＋∞）上为减函数，又2.2＞1.8，

∴＜。

【题后思考】当幂指数相同时，可直接利用幂函数的单调性来比较。

二、转化法

例2：比较的大小。

【思路分析】

题意分析：本题中三个数的底数都不相同，但指数可以转化为相同的，所以可以利用幂函数的性质解题。

解题过程：，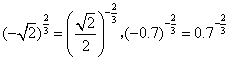

∵幂函数在（０，＋∞）上单调递减，且0.7＜＜1.21，

∴。

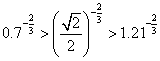【题后思考】当幂指数不同时可先转化为相同幂指数，再运用单调性比较大小。

三、中间值法

例3：比较0.8与0.9的大小。

【思路分析】

题意分析：由于这两个数的底数不同，指数也不同，所以可利用中间值来间接比较它们的大小。注意到这两个数的特点，中间值应选或。

解题过程：∵＞0，∴幂函数在（０，＋∞）上是增函数。

又0.8＜0.9，∴0.8＜0.9。

又0＜0.9＜1，指数函数在（0，＋∞）上是减函数，且＞，∴0.9＜0.9。

综上可得0.8＜0.9。

【题后思考】当底数不同且幂指数也不同，不能运用单调性比较大小时，可选取适当的中间值与两数分别比较，从而达到比较大小的目的。

知识点二：幂函数解析式的求法

一、利用幂函数的定义

例4：已知函数是幂函数，求此函数的解析式。

【思路分析】

题意分析：根据幂函数系数为1，幂指数为常数求解。

解题过程：∵是幂函数，

∴y可以写成如下形式（是常数）。

∴，解得。

当时，有（2为常数），（－1为常数）。

∴函数的解析式为或。

【题后思考】幂函数（x为自变量，是常数）的定义强调：系数为１，幂指数为常数。求出参数m后要注意检验幂指数是否为常数。

二、利用幂函数的图象

例5：若函数是幂函数，且图象不经过原点，求函数的解析式。

【思路分析】

题意分析：对于幂函数（是常数）而言，要使幂函数的图象不过原点，则指数≤0。

解题过程：∵函数是幂函数，且图象不经过原点，

∴，且。

∴或6。

∴函数解析式为或。

例6：已知幂函数（m∈Z）的图象与x轴、y轴都无交点，且关于原点对称. 求函数的解析式。

【思路分析】

题意分析：要解决本题，注意抓住幂函数的图象特点。

解题过程：∵幂函数的图象与x轴、y轴都无交点，

∴，解得。

又图象关于原点对称，且m∈Z，

∴m＝0。

∴。

【题后思考】解决与幂函数有关的综合题时，应抓住突破口，以上两例的突破口是图象的特点，只要抓住图象特点，将其转化为代数语言，就能顺利解题。

三、利用幂函数的性质

例7：已知幂函数（）是偶函数，且在（0，＋∞）上为增函数，求函数的解析式。

【思路分析】

题意分析：先求函数是幂函数的条件，再根据幂函数是偶函数即幂指数为偶数，然后判断增减性。

解题过程：∵是幂函数，∴，

解得t＝－1，t＝0或t＝1，

∴当t＝０时，，是非奇非偶函数，不满足条件. 当t＝1时，是偶函数，但在（0，＋∞）上为减函数，不满足条件。当时，满足题设条件。

综上所述，实数t的值为－1，所求解析式为。

【题后思考】涉及求与幂函数有关的参数问题，掌握幂函数的概念和性质是解题的关键. 解含参问题有时还应注意分类讨论。

提分技巧

幂函数的图象与性质记忆口诀：

如何分析幂函数，记住图象是关键，

虽然指数各不同，分类之后便简单，

函数奇偶看指数，奇母奇子奇函数，

奇母偶子偶函数，偶母非奇偶函数。

预习导学

一、预习新知

同学们，我们前面学习了指数函数，对数函数和幂函数，你们知道它们在实际生活中都有哪些应用吗？

二、预习点拨

反思探究：

探究任务一：今有一组实验数据如下：

	1.99	3.0	4.0	5.1	6.12
	1.5	4.04	7.5	12	18.01

现准备用下列函数中的一个表示这些数据满足的规律，其中最接近的一个是（）

A. B. C. D.

探究任务二：某家庭今年一月份、二月份和三月份煤气用量和支付费用如下表所示：

月份	用气量	煤气费
一月份	4m³	4元
二月份	25m³	14元
三月份	35m³	19元

该市煤气收费的方法是：煤气费＝基本费＋超额费＋保险费，若每月用量不超过最低限度Am³，只付基本费3元和每家每月的定额保险C元（不低于1元），若用气量超过Am³，则超过部分每立方米付B元，又知保险费C不超过5元，根据上面的表格求A，B，C。

同步练习

（答题时间：45分钟）

1. 使x²＞x³成立的x的取值范围是（）

A. x＜1且x≠0 B. 0＜x＜1 C. x＞1 D. x＜1

2. 若四个幂函数y＝，y＝，y＝，y＝在同一坐标系中的图象如图，则a、b、c、d的大小关系是（）

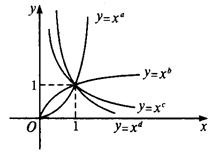
A. d＞c＞b＞a B. a＞b＞c＞d

C. d＞c＞a＞b D. a＞b＞d＞c

3. 在函数y＝，y＝2x³，y＝x²＋x，y＝1中，幂函数有（）

A. 0个 B. 1个 C. 2个 D. 3个

4. 下列函数①②③④⑤，其中是幂函数的是（）

A. ①⑤ B. ①②③ C. ②④ D. ②③⑤

5. 下列函数中，与函数有相同定义域的是（）

A. B. C. D.

6. 下列说法中正确的是（）

A. 当＝0时，函数的图象是一条直线

B. 幂函数的图象都经过（0，0），（1，1）

C. 幂函数的图象不可能在第四象限内

D. 若幂函数为奇函数，则它在定义域内是增函数

7. 设函数，则＝_________。

8. 若幂函数的图象经过点，则＝________。

9. 求函数的定义域和值域。

10. 已知幂函数f（x）＝（p∈Z）在（0，＋∞）上是增函数，且在其定义域内是偶函数，求p的值，并写出相应的函数f（x）。

试题答案

1. A 解析：利用幂函数图象解题。

2. B 解析：比较幂函数在第一象限内的幂指数的大小与图象的关系。

3. B 解析：根据幂函数的定义解题。

4. C 解析：同上。

5. A 解析：分别求各函数的定义域。

6. C 解析：考查幂函数的图象与性质。

解析：

解析：设，由题意，得，解得。

所以，。

9. 解析：由。

又

10. 解析：因为幂函数f（x）＝在（0，＋∞）上是增函数，所以－p²＋p＋＞0，解得－1＜p＜3。

又幂函数在其定义域内是偶函数且p∈Z，所以p＝1，相应的函数f（x）＝x²。