【本讲教育信息】

一. 教学内容：

多边形的认识及面积

［知识梳理］

（一）平行四边形：

1. 平行四边形的特点：

（1）定义：两组对边分别平行的四边形叫做平行四边形。

（2）特点：

·平行四边形对边平行且相等。

·平行四边形对角相等，同侧两角之和是180°，内角和为360°。

·平行四边形具有不稳定性（易拉动变形）。

·长方形、正方形是特殊的平行四边形。

·平行四边形的名称（底和高）：平行四边形有无数条高。

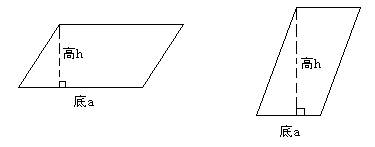
2. 面积公式：

平行四边形面积＝底×高

（二）梯形

1. 梯形的特点：

（1）定义：一组对边平行而另一组对边不平行的四边形叫做梯形。

或（只有一组对边平行的四边形叫做梯形。）

（2）特点：

互相平行的一组对边，分别叫做梯形的上底和下底，不平行的一组对边叫做梯形的腰，从上底的任意一点向下底引垂线，这点到垂足间的线段叫做梯形的高。

（梯形有无数条高）

·

2. 面积公式：

梯形面积＝（上底＋下底）×高÷2

S＝（a＋b）×h÷2

2个完全相同的梯形

（三）三角形

1. 三角形的特点：

（1）定义：由三条线段顺序首尾相接组成的图形叫做三角形。

（2）特点：组成三角形的每条线段叫做三角形的边，每两条线段的交点叫做三角形的顶点。

三角形有三条边、三个顶点、三个内角。

·三角形任意两边长度之和大于第三边。

·三角形具有稳定性（不会变形）。

·三角形内角和是180°。

·三角形分类：按边分

按角分

·三角形的底和高

试一试：任选一条边做底，画出相应的高。

锐角三角形

直角三角形

两条直角边互为底和高

钝角三角形：

2. 三角形面积：

三角形面积＝底×高÷2

S＝a×h÷2

【典型例题】

例1. 一个等腰三角形的顶角是50°，求两个底角各是多少度？

分析与解：等腰三角形两个底角度数相等，三角形内角和是180°。

（180－50）÷2＝65°

答：两个底角都是65°。

例2. 判断对错，并说明理由。

（1）有一个角是锐角的三角形就一定是锐角三角形。（ ）

（2）两个面积相等的三角形可以拼成一个平行四边形。（ ）

（3）等底等高的两个三角形面积一定相等。（ ）

分析与解：

（1）只有三个角都是锐角的三角形才是锐角三角形，所以错。

（2）面积相等不一定形状相同，只有面积、形状都完全相同才能拼成一个平行四边形，所以错。

（3）S＝a×h÷2，面积决定于底和高两个条件。这两个条件都相等，计算出的结果也一定相等，所以是正确的。

【模拟试题】（答题时间：25分钟）

1. 请标出下面图形的底和高，并测量出数据。（任选一种）

2. 一个直角三角形，其中一个锐角是30°，另一个锐角是多少度？

3. 判断：

（1）三根分别长3cm、5cm、10cm的木棍可以围成一个三角形。（ ）

（2）一个三角形不可能有2个钝角。（ ）

（3）一个梯形可以画无数条高。（ ）

4. 数一数下图中共有多少个三角形，多少个平行四边形？

（ ）个三角形

（ ）个平行四边形

（ ）个梯形

【试题答案】

1. 请标出下面图形的底和高，并测量出数据。（任选一种）

答：答案不唯一（略）

2. 一个直角三角形，其中一个锐角是30°，另一个锐角是多少度？

180°－90°－30°＝60°

答：另一个锐角是60°。

3. 判断：

（1）三根分别长3cm、5cm、10cm的木棍可以围成一个三角形。（×）

（2）一个三角形不可能有2个钝角。（√）

（3）一个梯形可以画无数条高。（√）

4. 数一数下图中共有多少个三角形，多少个平行四边形？

（4）个三角形

（3）个平行四边形

（2）个梯形