【本讲教育信息】

一. 教学内容：

平面图形、空间图形、观察物体

二. 教学目标：

1. 认识常见的平面图形和空间图形，能用自己的语言描述它们的某些特征，知道平面图形与空间图形的联系和区别。

2. 了解多面体的顶点数、面数、棱数之间的关系。

3. 通过实例，了解视点、视角、盲区的意义，并能在简单的平面图和立体图中表示。

4. 知道物体的阴影怎么形成的，并能根据光线的方向辨认实物的阴影。

三. 教学重点、难点：

重点：认识各种平面图形和空间图形，弄清它们的区别和联系，根据影子确定光源位置，根据光源位置画出影子。

难点：多面体的顶点数（V），棱数（E），面数（F）之间的关系（欧拉公式）的理解与应用，光源的确定。

四. 教学知识要点：

1. 常见的平面图形有三角形、四边形、五边形、六边形、八边形……这些平面图形称为多边形、正三角形、正四边形、正五边形……，它们都是各条边相等的多边形，统称为正多边形，常见的平面图形还有圆、扇形等。多边形是由线段围成的封闭图形，圆是由曲线围成的封闭图形，扇形是由曲线和线段围成的图形，每一个多边形都可以分割成若干个三角形。

2. 空间图形有由平面图形围成的，常见的有六面体（长方体、正方体都是六面体，它们由六个平面图形——长方形或正方形所围成）、正四面体、正八面体、正十二面体、正二十面体，这些空间图形称为多面体，常见的空间图形还有球、圆柱、圆锥、圆台等对于多面体有V＋F－E＝2。

3. 观察同一个物体，观察者距离物体的远近不同，观察到物体的形状是不同的。

4. 观察同一个物体，观察物体的视线角度不同，观察到物体的形状也会有所不同。

5. 光源发出的光照到不透明的物体上，在物体的背后形成一个光线照不到的或部分光线照不到的黑暗区域，成为物体的投影。

【典型例题】

例1. 指出下列图形的名称，它们是平面图形还是空间图形？

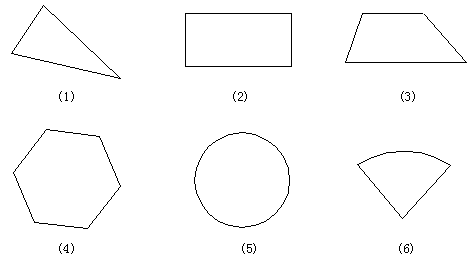
分析：这些图形都是由线段或曲线在同一平面内围成的封闭图形，属于平面图形。

解：

例2. 指出下列图形的名称，它们是平面图形还是空间图形？

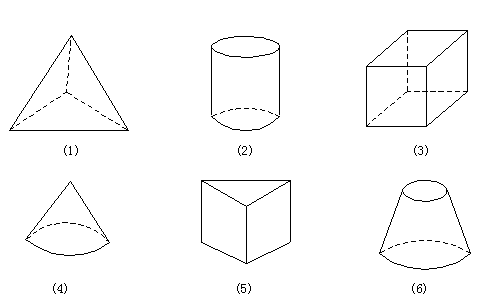
分析：这些图形由一些平面图形和曲面围成，属于空间图形。

解：图（1）为正四面体，图（2）为圆柱，

图（3）为正方体，图（4）为圆锥，

图（5）为三棱柱，图（6）为圆台。

它们都是空间图形。

例3. 如图所示是某些多面体的平面展开图，说出这些多面体的名称。

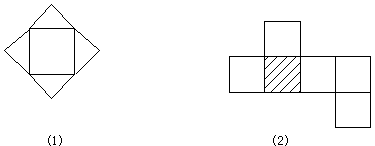
分析：图（1）可以把四周的四个三角形折合封闭围成一个四棱锥或者说一个五面体，图（2）中可把有阴影的正方形不动，其余正方形折合封闭围成六面体或者说一个正方体。

解：图（1）是一个五面体的展开图。

图（2）是一个正方体的展开图。

例4. 填空：

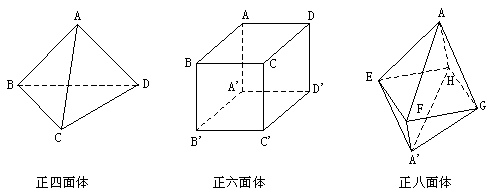
（1）正四面体的顶点数V＝4，面数F＝4，棱数E＝6。

（2）正六面体的顶点数V＝8，面数F＝6，棱数E＝12。

（3）正八面体的顶点数V＝6，面数F＝8，棱数E＝12。

多面体的顶点数用V表示，面数F表示，棱数E表示。

则有一规律可用一个公式来表示：（欧拉公式）

即V＋F－E＝2。

分析：把正四面体、正六面体、正八面体的图作出，再数顶点个数V，面数F，棱数E，再填空。

例5. 一个多面体的棱数E为30，顶点数V为20，它有多少个面？

解：设面数为F，则

即

答案：它有12个面

例6. 确定图中路灯的位置，画出第三根旗杆的影子。

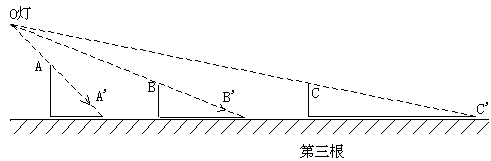
分析：在图中相应的点上标上A，A’，B，B’，C，连AA’，BB’两线延长交于O，O点处为灯的位置，连OC，并延长交路上一点为C’。图中C’点到第三根旗杆脚的那条线段则为第三根旗杆的影子。

例7. 观察一幢高层楼房，如果在你站的位置正好能看到楼房的一至三层，若想看到更高的几层楼？你是应该由你站的位置向前走还是往后退？

分析：如图所示不管你在哪个位置，你的视角不变的，若向前走，看的楼层少了，如（1）的位置，若往后退，退到（2）的位置，则看的楼层高些，多些。

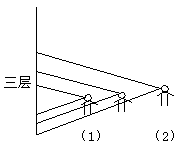
解：若想看到更高的楼层，要往后退。

【模拟试题】（答题时间：25分钟）

一. 填空题：

1. 正十二面体的顶点数V＝_________，面数F＝_________，棱数E＝_________。

2. 一个多面体的顶点数V，面数F，棱数E三者之间的关系式为_________。

3. 在同一平面内，由一些_________围成的封闭图形称为平面图形。

4. 圆柱是_________图形，它的两个底是_________，侧面为_________。

5. 把一个三棱锥切去一个角，看到的平面图形为_________。

二. 解答题：

1. 有一个正多面体，它的顶点数、面数、棱数的比为2：2：3，它是一个正几面体？并画出它的图形。

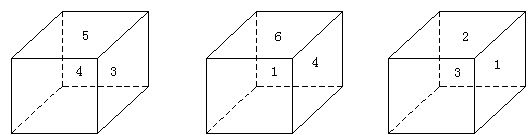
2. 一个正方体木块，六个面上分别写着1、2、3、4、5、6，从三个不同的角度观察的结果如图所示，这个正方体每两个相对的面上的数各是几？

3. 有一个正方形花坛，现要把它分成面积相同的八块，分别种上不同颜色的花。

（1）如果要求这样分成的八块形状相同，请设计几种方案来？

（2）如果要求八块中的每四块形状相同，应如何设计？

【试题答案】

一. 填空题：

1. 20，12，30

2.

3. 线段或曲线

4. 空间，圆，曲面

5. 三角形

二. 解答题：

1. 解：设

则

所以它为正四面体，图形如下：

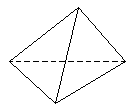
2. 解：由图可知与“4”相对的面的数字不可能为3、5、1、6，所以与“4”相对的为“2”，同理可推与“3”相对的面的数字为“6”，与“5”相对的面的数字为“1”。

3. 答案略。（答案不唯一）