![]()
【本讲教育信息】
一. 教学内容:
密铺和折叠
知识目标:
1. 通过实践活动和数学分析,会判断某种平面图形能否密铺平面。
2. 能把立体图形展开成平面图形,也能把平面展开图想象成立体图形。
能力目标:
1. 培养学生动手拼图的实验能力和利用数学知识进行简单的数学分析的能力。
2. 培养学生空间想象能力和分析判断能力。
情感目标:
通过本节课的学习,让同学们体验应用数学知识解决生活中实际问题的乐趣,增强学好数学的信心。
【知识要点】
1. 密铺定义的理解
教材上说:将一块地面不留缝隙也不重叠地铺满,也就是密铺,对于这句话我们很容易的总结出密铺的特点:(1)不留缝隙,(2)不重叠。但是通过实践研究我们发现只满足这两条还不够,尤其是在研究任意四边形能否密铺的时候表现的比较明显。其实密铺还应该有一个特点那就是:铺满,也就是说,说明某种平面图形能否密铺除了满足上述2个特点外,不能说这种图形在某一个顶点处,拼成了360°就一定能密铺平面,还要注意到这种图形能否在各个顶点处能继续密铺下去,也就是说能否铺满平面。所以说能密铺的平面图形必须满足以下3个特点:
(1)不留缝隙,
(2)不重叠,
(3)铺满。
这一点同学们一定要很好的体会。
2. 平面图形和立体图形的互相转化是折叠这一节课主要研究的问题,对于一个立体图形可以有不同的平面展开图,但对于一个平面展开图形却只能围成一个立体图形。另外在图形的互相转化过程中要有意识的培养自己的空间想象能力。
【典型例题】
例1:形状相同、大小相等的三角形可以密铺平面吗?
分析与解:对于形状相同和大小相等的三角形是可以密铺的,因为我们知道形状相同和大小相等的平行四边形是一定能密铺平面的,那么两个大小相等、形状相同的三角形一定
能拼成一个平行四边形,所以研究三角形密铺问题实质是研究平行四边形的密铺问题。如右图所示:
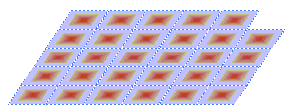
例2:用边长相等的正方形和正三角形可以密铺平面吗?
分析与解:用边长相等的正三角形和正方形可以密铺平面,首先我们注意到正三角形每个内角都是60°,正方形的每一个内角都是90°,所以总可以在一个顶点处用3个正三
角形的内角和2个正方形内角拼成一个360°的角,而且正三角形和正方形的边长相等,所以边长相等的正三角形和正方形一定能密铺平面。如右图所示。
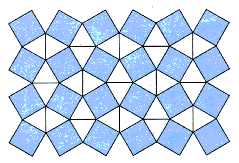
例3:形状相同、大小相等的任意四边形可以密铺平面吗?
分析与解:形状相同,大小相等的任意四边形是可以密铺平面的。因为四边形的内角和是360°,这样4个形状相同,大小相等的四边形是总会有4个内角拼在一起构成一个360°的角,所以一定能密铺平面,但是在具体铺的过程中一定要注意要让相等的边重合在一起,否则是不能密铺整个平面的。如右图所示。
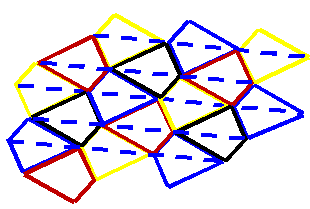
例4:正方体有6个面,每个面上分别写着1—6的数字,而且两个相对面的两个数的和是7,下面是正方体不同的平面展开图,请填出空格内的数。

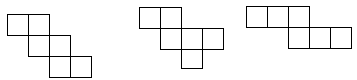
分析:首先要注意到以上图形是正方体的平面展开图,在填数之前,一定要先通过空间想象,确定哪两个面还原回正方体后可能会成为相对的面,这一点至关重要,至于怎样确定相对面,要因人而异,个人有个人的方法,建议同学们先尝试着填一填,然后再看答案,然后对比找出自己的不足之处,对培养空间想象能力是很有帮助的。
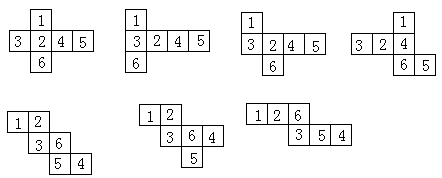
例5:有一块宽是16厘米的长方形铁皮,在四个角上剪去边长为4厘米的正方形后,焊成一个无盖的盒子,已知盒子的体积是768立方厘米,求这块铁皮原来的面积。

分析与解:要求这块铁皮的面积,已经知道了它的宽是16厘米,所以只需求出长是多少厘米即可,首先要想象出焊成的长方体盒子是一个什么样子,它的长应该是原来铁皮的长—2个4厘米得到,它的宽应该是原来铁皮的宽16-2个4厘米得到,它的高应该是4厘米。题中已经告诉了体积。所以列一个简单的方程即可。
解:设这块铁皮原来的长是x厘米,列方程得
(x-4×2)×(16-4×2)×4=768
解得 x=32
铁皮面积:32×16=512(平方厘米)
答:这块铁皮的原来的面积是512平方厘米。
注意:这道题也可以用算术方法解,同学们自己可以试一试。
例6:下图是一茶叶桶外包装展开图,它围成的茶叶桶的大小与实际大小的比是1:10。
⑴折成的茶叶桶的体积是多少?
⑵这个茶叶桶的实际体积是多少?
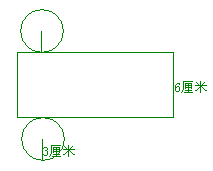
分析与解:第一问要马上能想象出这个茶叶桶是一个圆柱体,那么圆柱体的体积公式为:底面积×高,底面积即是圆的面积,题中告诉了半径,所以面积可求,圆柱体的高就是展开图中长方形的长,所以
解:⑴折成的茶叶桶的体积是:32×π×6=54π(立方厘米)
⑵这个茶叶桶的实际体积是:54π×10=540π(立方厘米)
注意:这里要注意到第二问求茶叶桶的实际体积时,是在已知围成的茶叶桶的大小与实际茶叶桶的大小的比是1:10的前提下,如果已知条件变成展开图的大小与实际的大小的比1:10的话,那么在计算实际体积时,就要把图中的尺寸先按比例放大10倍后,再按照体积公式进行计算,这一点同学们要注意体会。
例7:以下两平面展开图,围成立体图形后,那一个体积大一些?大多少?
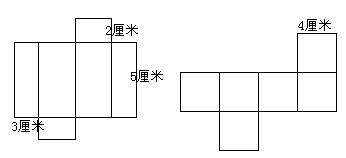
分析与解:要计算围成立体图形后体积的大小,就要先想象出围成的立体图形是什么图形,它们的外形尺寸是多少,通过观察,想象我们不难发现这两个平面展开图围成立体图形后一个是长方体,一个是正方体。其中长方体的长为:5厘米,宽为:3厘米,高为:2厘米。正方体的边长为4厘米。
解:长方体的体积是:5×3×2=30(立方厘米)
正方体的体积是:43=64(立方厘米)
64-30=34(立方厘米)
答:正方体的体积大一些,大34立方厘米。
【模拟试题】(答题时间:20分钟)
选择题:下面各题中左面图形能围成的图形是:
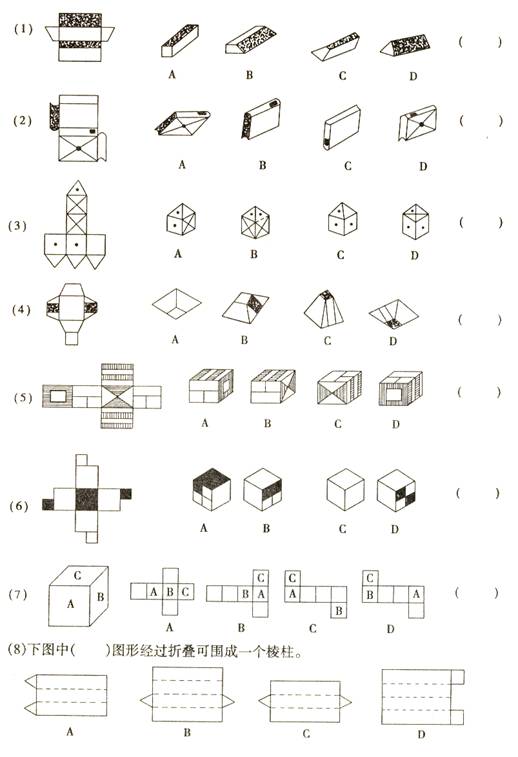
![]()
【试题答案】
⑴
C ⑵ A ⑶ D ⑷ B
⑸ C ⑹ D ⑺ D ⑻ C