![]()
【本讲教育信息】
一. 教学内容:
相似三角形和三角形相似的条件
1. 了解相似三角形、相似比的含义.
2. 掌握两个三角形相似的判断条件,并能够运用三角形相似的判断方法解决一些简单的问题.
二. 知识要点:
1. 相似三角形
(1)相似三角形:对应角相等、对应边成比例的两个三角形叫做相似三角形.
(2)相似比:相似三角形对应边的比叫做相似比.
(3)表示方法:用符号“∽”来表示相似,读作“相似于”.如图所示,△ABC和△A’B’C’相似,记作“△ABC∽△A’B’C’”,读作“△ABC相似于△A’B’C’”.

说明:
(1)这个定义告诉我们:①如果两个三角形的角对应相等、边对应成比例,那么这两个三角形相似;②如果两个三角形相似,那么它们的对应角相等、对应边成比例.
(2)相似比是有顺序的.例如:若△ABC∽△A’B’C’,相似比为k,则△A’B’C’∽△ABC,那么相似比为.
2. 三角形相似的条件
(1)如果两个三角形的两角对应相等,那么这两个三角形相似.
例如:如图所示,若∠A=∠A’,∠B=∠B’,则△ABC∽△A’B’C’;
若∠A=∠A’,∠C=∠C’,则△ABC∽△A’B’C’;
若∠C=∠C’,∠B=∠B’,则△ABC∽△A’B’C’.
说明:只要有两对角对应相等,这两个三角形就相似.“对应”不一定非得是“A对A’,B对B’,C对C’”.
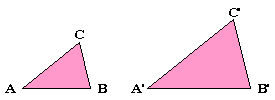
(2)两边对应成比例,且夹角相等的两个三角形相似.
例如:如上图所示,若=,∠B=∠B’,则△ABC∽△A’B’C’;
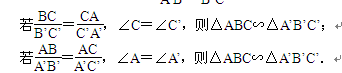
(3)三边对应成比例的两个三角形相似.
![]()
三. 重点难点:
本讲重点是相似三角形的定义和三角形相似的条件,难点是应用三角形相似的三个条件解决一些问题.

评析:(1)①求相似比时要注意顺序,哪个三角形在前,它的对应边就作为比的前项.②相似比实际上反映的是一个图形的放大或缩小,相似比大于1,说明图形被放大;相似比小于1,说明图形被缩小;相似比等于1,说明两个图形全等.③若△ABC与△A'B'C'的相似比为k,则△A'B'C'与△ABC的相似比为.(2)找两个相似三角形的对应边、对应角的方法有两种:①如果给出相似表达式,就先找对应顶点,再找对应边、对应角.②如果已知对应角,那么对应角所对的边就是对应边;如果已知对应边,那么对应边所对的角就是对应角.找两个相似三角形的对应边还有一个原则:大边对大边,小边对小边.
例3. 如图所示,平行四边形ABCD中,G是BC延长线上一点,AG与BD交于点E,与DC交于点F,则图中相似的三角形共有( )
A.3对 B.4对 C.5对 D.6对
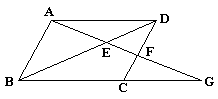
分析:由AD∥BG,可得∠DAE=∠G,∠ADB=∠DBG,可推出△AED∽△GEB,同理可推出△AFD∽△GFC;由AB∥DC可得到△AEB∽△FED和△ABG∽△FCG,由相似图形的传递性,知△GAB∽△AFD,又△ABD∽△CDB,∴图中共有6对相似三角形,故正确答案为D.
解:D
评析:充分利用题目中的条件,如平行、垂直等推出相等的角,如公共角,对顶角等.
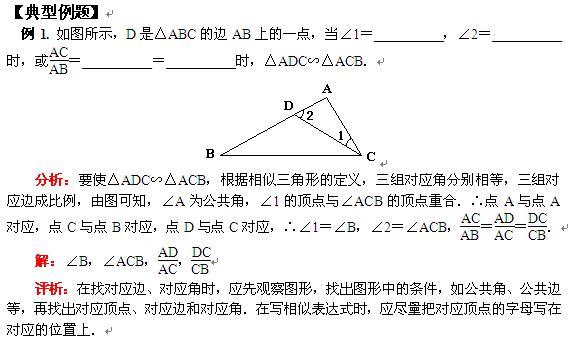
例4. 如图所示,BC平分∠ABD,AB=4,BD=5,当BC=__________时,△ABC∽△CBD.
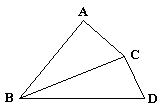

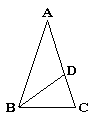
分析:有一个角为36°的等腰三角形,它的底角是72°,而BD是底角的平分线,故∠CBD=36°,则可推出△ABC∽△BCD,进而由相似三角形对应边成比例推出线段之间的比例关系.
解:(1)因为∠A=36°,AB=AC,所以∠ABC=∠C=72°.
又因为BD平分∠ABC,所以∠ABD=∠CBD=36°.
所以AD=BD=BC,所以△ABC∽△BCD.

例6. 为了测量校园内一棵不可攀登的树的高度,学校数学兴趣小组做了如下的探索:
如图所示,把镜子放在离树(AB)8.7米的点E处,然后沿着BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算出树的高度.(精确到0.1米)


【方法总结】
1. 三角形相似的条件有三个:①两角对应相等的两个三角形相似;②两边对应成比例且夹角相等的两个三角形相似;③三边对应成比例的两个三角形相似.
2. 相似三角形判定方法的作用:①可以用来判定两三角形相似;②间接说明角相等,线段成比例;③间接为计算线段长度及角的大小创造条件.
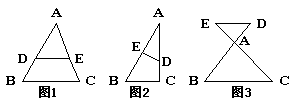
3. 有关三角形相似的基本图形:①如图1所示,若DE∥BC,则△ADE∽△ABC;②如图2所示,若∠ADE=∠B,则△ADE∽△ABC;③如图3所示,若DE∥BC,则△ADE∽△ABC.
【预习导学案】
(相似三角形和相似多边形的性质)
一. 预习前知
1. 相似三角形的对应边__________,对应角__________.
2. 已知△ABC∽△A’B’C’,AB=3,BC=4,A’B’=5,∠A=80°,∠B=30°,求B’C’的长与∠C’的度数.
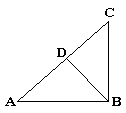
3. 如图所示,在△ABC中,∠B=90°,AB=BC,点D是AC的中点.找出图中的相似三角形(不包括全等三角形),并求出其相似比.
二. 预习导学
1. 已知△ABC∽△A’B’C’,C△ABC=12,=2,求C△A’B’C’.
2. 已知△ABC∽△A’B’C’,S△ABC=12,=2,求S△A’B’C’.
3. 如图所示的两个四边形相似,找出图中的对应角、对应边、并用比例式表示.
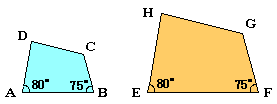
4. 两个相似多边形的相似比为2∶3,则它们周长的比为__________,面积的比为__________.
反思:(1)相似三角形有什么性质?
(2)相似多边形有什么性质?
【模拟试题】(答题时间:50分钟)
一. 选择题
1. 已知△ABC∽△A'B'C',如果∠A=75°,∠B=25°,则∠C'的度数为( )
A.80° B.70° C.60° D.50°
2. 下列说法中正确的个数是( )
①所有的直角三角形都相似;②所有的等腰三角形都相似;③所有的等腰直角三角形都相似;④所有的等边三角形都相似.
A.1个 B.2个 C.3个 D.4个
3. △ABC∽△A'B'C',且相似比为,△A'B'C'∽△A''B''C'',且相似比为,则△ABC与△A''B''C''的相似比为( )
![]()
4. 具备下列各组条件的△ABC和△A'B'C',不能判定它们相似的是( )
A.∠A=∠A',∠B=∠B' B.∠A=∠A',∠B=∠C'
C.∠A=∠B',∠B=∠C' D.∠A=∠A',∠B=∠A'
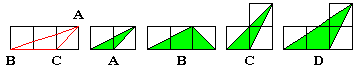
5. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
*6. 已知,如图所示,D、E是△ABC的边AB、AC上的点,且△AED∽△ABC,∠A=35°,∠C=85°,则下列结论错误的是( )
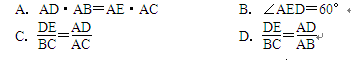
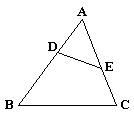
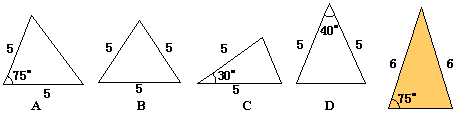
7. 下列4个三角形中,与右边三角形相似的是( )
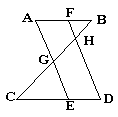
**8. 如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则图中共有相似三角形( )
A.4对 B.5对 C.6对 D.7对
二. 填空题
1. 若两个三角形的相似比是1,则这两个三角形__________.
2. 已知△ABC∽△DEF,则∠A=__________,∠B=__________,∠C=__________,=__________=__________.
3. △ABC的各边之比为2∶5∶6,与其相似的另一个△A'B'C'的最大边长为18cm,那么△A'B'C'的最小边长为__________.
4. 如图,在△ABC中,DE∥BC,若AD=1、DE=2、BD=3,则BC=__________.
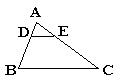
5. 如图所示,△ABC∽△DBE,且AD=AB,则△ABC与△DBE的相似比为__________.
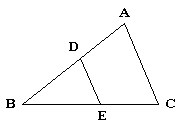
6. 如图所示,(1)若=__________,则△AEF∽△ABC,理由是__________;(2)若__________∥__________,则△AEF∽△ABC.

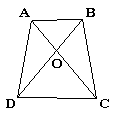
*7. 如图所示,AC、BD相交于O,若给出__________=__________,则可以使△AOB∽△DOC,若给出DC2=DO·DB,则可以使__________∽__________.
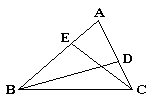
**8. 如图所示,△ABC中,点D、E分别在AC、AB边上,要使△ABD∽△ACE,已具备的条件是__________,还需要添加的条件是__________或__________或__________.
三. 解答题
1. 依据下列各组条件判定△ABC与△A’B’C’是否相似,并说明理由.
(1)∠A=45°,AB=12cm,AC=15cm,∠A’=45°,A’B’=16cm,A’C’=20cm;
(2)∠B=80°,AB=1.5cm,BC=2cm,∠B’=80°,A’B’=2.8cm,B’C’=2.1cm.
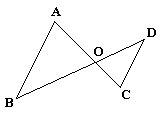
2. 如图所示,若∠A=∠C,那么△OAB与△OCD相似吗?OA·OD=OB·OC吗?为什么.
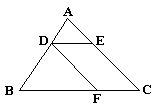
3. 如图所示,已知△ADE∽△ABC,△DBF∽△ABC,AD=4cm,BD=8cm,DE=5cm,求BF的长.
*4. 请你制作两个三角形框架,其中一个三角形框架的三边长分别为4、5、6,另一个三角形框架的一边长为2,如何选料可使这两个三角形相似?
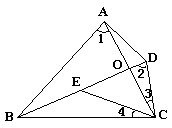
**5. 四边形ABCD的对角线AC、BD相交于点O,∠1=∠2,∠3=∠4,指出图中有哪些相似三角形,并说明理由.如图所示.
![]()
,△CDO 8. ∠A=∠A,