【本讲教育信息】
一、教学内容：
等腰三角形、直角三角形以及轴对称图形的性质
1、等腰三角形的性质，判定方法，等边三角形的性质与判定
2、30°角的直角三角形的性质与判定
3、轴对称图形的性质
二、学习重、难点：
等腰三角形、直角三角形的性质与判定是本节课的重点；也是难点
三、知识要点讲解：
【知识回顾】
1、等腰三角形的腰、底边、顶角、底角
注：
等边三角形也叫正三角形，它是特殊的等腰三角形，即底边和腰相等的等腰三角形。
2、三角形的中线、高线、角平分线————是线段，各有三条。
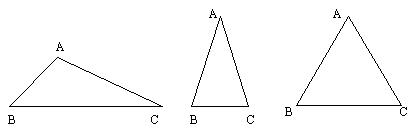
3、画出三个三角形：
（1）三边都不相等； （2）有两边相等； （3）三边都相等。
【等腰三角形与等边三角形的性质与判定】
思考：三个三角形中有几个轴对称图形？若是轴对称图形，对称轴是什么？
结论：不等边三角形不是轴对称图形；等腰三角形、等边三角形都是轴对称图形。
想一想：等腰三角形是轴对称图形，找出它的对称轴。
（1）是顶角平分线所在的直线吗？
（2）是底边中线所在的直线吗？
（3）是底边上的高所在的直线吗？
如图所示，∠1=∠2，由于AB = AC，沿AD对折△ABC，能使△ABD与△ACD重合，这时有BD=CD，
，∠B=∠C
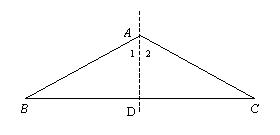
因此，等腰三角形的对称轴可以说是：顶角平分线所在的直线或底边中线所在的直线或底边上的高所在的直线。
由于AD即是BC边的中线又是BC边的高，因此，AD所在直线就是BC的中垂线，因此，等腰三角形的对称轴也可以说成是底边的中垂线。
1、由等腰三角形对称性，发现等腰三角形特征。
（1）等腰三角形“三线合一”
即等腰三角形的顶角平分线、底边中线、底边的高互相重合。
（2）等腰三角形的两个底角相等。
2、等边三角形有什么特征？
等边三角形有三条对称轴，每一个角的平分线所在的直线都是它的对称轴。
等边三角形每个角都相等，而且都等于60度。
想一想：
1、如果一个三角形有两条边相等，那么这两条边所对的角也相等，反过来，如果一个三角形有两个角相等，那么这两个角所对的边也相等吗？
2、你能用较严密的语言说明结论为什么成立吗？
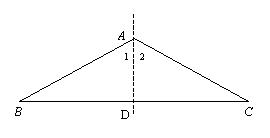
结论：这实际上是等角对等边，是等腰三角形的判定方法之一
应用：∠B=∠C
AB=AC
结论：如果一个三角形有两个角相等，那么这两个角所对的边也相等。简称：等角对等边
想一想：
1、如果三角形的三个内角都相等，那么这个三角形是什么三角形？为什么？
2、如果一个等腰三角形有一个角是60°，那么这个三角形是什么三角形？为什么？
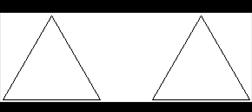
性质：如果三角形的三个内角都相等，那么这个三角形是等边三角形。
如果一个等腰三角形有一个角是60°，那么这个三角形是等边三角形。
拼一拼、想一想：
由两个全等的30°的直角三角形拼在一起，你能得到什么结论？
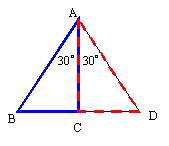
解：△ABC是等边三角形，有AB=AD=BD，BC=
BD=AB，及CD=AD的关系。从而得到30°角的直角三角形的特征：
直角三角形的性质：
在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。
【典型例题】
例1、①等腰三角形的两边长为3和6，则这个三角形的周长为（ ）.
（A）9 （B）12 （C）15 （D）12或15
②等腰三角形的两条边长分别为
（A）
③如下图，PQ为Rt△MPN斜边上的高， ∠M=45°，则图中等腰三角形的个数是（ ）
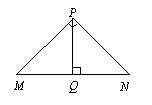
（A） 1个 （B） 2个 （C） 3个 （D） 4个
例2、已知：如下图，P，Q是△ABC边上BC上的两点，且BP=PQ=QC=AP=AQ，求∠BAC的度数.
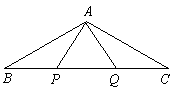
解：∵PQ=AP=AQ ∴∠APQ=∠PQA=∠QAP=60° ∴∠APB=∠AQC=120°
∵AP=PB、AQ=QC ∴∠B=30°、∠C=30° ∴∠BAC=120°
例3、已知AE平分∠DAC，AE∥BC，那么AB=AC吗？请简要说明理由.
答：△ABC是等腰三角形
解：∵AE平分∠DAC ∴∠DAE=∠EAC ∵AE∥BC ∴∠DAE=∠B、∠EAC=∠C
∴∠B=∠C ∴ AB=AC
例4、如图，在△ABC中，AB＝AC，BD＝AD，DC＝AC，则∠B＝_______．
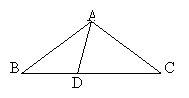
解：∵AB＝AC，BD＝AD ∴∠C=∠B=∠BAD ∵ DC＝AC ∴∠ADC=∠DAC
设：∠C=∠B=∠BAD=x，则：∠ADC=∠DAC=2x
∵∠DAC＋∠ADC＋∠C =180° ∴x+2x+2x=180° ∴x=36° 即：∠B=36°
例5、如图，已知直角
中，
，
，角平分线
交
于
，那么
是不是等腰三角形？能说说你的理由吗？
答案：是等腰三角形．
理由：由平分
，得
，又因为
，所以
，而
，故
．是等腰三角形．
【课堂小结】
本节课我们主要研究了等腰三角形以及特殊的等腰三角形——等边三角形的性质、判定，学习了30°角的直角三角形的性质
性质：等腰三角形是轴对称图形，它的对称轴有三种表述形式。
等腰三角形的顶角平分线、底边上的中线、高互相重合（“三线合一”）。
等腰三角形两底角相等。
等边三角形是轴对称图形，它有三条对称轴。
等边三角形每一个都等于60°。
判定：等角对等边。有一个角等于60°的等腰三角形是等边三角形，三个角都相等的三角形是等边三角形。
性质与判定的互逆性——逆向思考问题的思想方法。
【模拟试题】（答题时间：60分钟）
一、选择题：
*1、等腰三角形的周长为13，其中一边长为3，则该等腰三角形底边长为（ ）.
（A） 7 （B） 3 （C）7或3
（D）5
2、如下图，在△ABC中，AB=AC，∠A=50°，P是△ABC内一点，∠PCB=∠PCA，且∠PBC=∠PBA，则∠BPC的度数为（ ）.
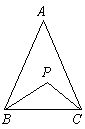
（A）115°
（B）100°
（C）130°
（D）140°
3、至少有两边相等的三角形是（ ）.
（A）等边三角形
（B）等腰三角形
（C）等腰直角三角形 （D）锐角三角形
4、在线段、角、等腰三角形、正三角形中，是轴对称图形的有（ ）．
（A）1个 （B）2个 （C）3个 （D）4个
*5、下列说法中正确的是（ ）
（A）角是轴对称图形，它的平分线就是对称轴
（B）等腰三角形的内角的平分线，中线和高三线合一
（C）直角三角形不是轴对称图形
（D）等边三角形有三条对称轴
6、等腰三角形的一个内角是50°，那么其它两个内角分别是（ ）
（A）50°和80° （B）65°和65°
（C）50°和80°或65°和65° （D）无法确定
*7、等腰三角形顶角是84°，则一腰上的高与底边所成的角的度数是（ ）.
（A）42°
（B）60°
（C）36°
（D）46°
*8、如下图，△ABC中，AD⊥BC，AB=AC，∠BAD=30°，且AD=AE，则∠EDC等于（
）
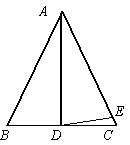
（A）10°
（B）12.5°
（C）15° （D）20°
*9、如下图，PM=PN，MQ为△PMN的角平分线，若∠MQN=72°，则∠P的度数是（ ）.
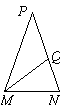
（A）18°
（B）36°
（C）48° （D）60°
**10、已知△ABC中，AB=AC，AD⊥BC于D，△ABC的周长为
（A）
*11、如下图，在△ABC中，AB=AC， ∠A=36°，BD、CE分别是∠ABC、∠ACB的平分线，则图中等腰三角形的个数为（ ）.
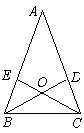
（A）12 （B）10 （C）9 （D）8
12、如果三角形一边的中线和这边上的高重合，那么这个三角形是（ ）.
（A）等边三角形 （B）等腰三角形 （C）锐角三角形 （D）钝角三角形
*13、在下列命题中：①有一个外角是120°的等腰三角形是等边三角形；
②有两个外角相等的等腰三角形是等边三角形；
③有一边上的高也是这边上的中线的等腰三角形是等边三角形；
④三个外角都相等的三角形是等边三角形.
其中正确的是（ ）.
（A）4个 （B）3个
（C）2个 （D）1个
14、在△ABC中，∠B=∠C=40°，D、E是BC上的两点，且∠ADE=∠AED=80°，则图中共有（ ）等腰三角形.
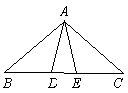
（A）6个 （B）5个
（C）4个
（D）3个
二、填空题：
1、在△ABC中， ∠A=∠B=∠C，则△ABC是_____三角形；
*2、在△ABC中， ∠ABC=∠ACB， ∠ABC与∠ACB的平分线交于点D，过D作EF∥BC，交AB于E，交AC于F，则图中的等腰三角形有____个，分别是______.
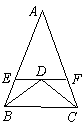
3、等腰三角形的对称轴是_____，等边三角形有_____条对称轴，正方形有_____条对称轴，圆有_____条对称轴．
4、三角形三条角平分线的交点到_____的距离相等．
*5、等边三角形的两条中线相交所成的钝角的度数是_____．
三、解答题：
1、在△ABC中，AD是∠BAC的平分线，过C作CE∥AD交BA的延长线于点E，则线段AE与AC是否相等，为什么？
2、△ABC是等腰三角形，AB=AC，D为底边BC上一点，DE∥AB且交AC于E，请判断△EDC是什么三角形？并说明理由.
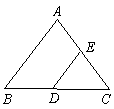
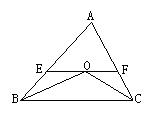
3、如图所示，△ABC中，∠ABC与∠ACB的角平分线相交于点O，过O作EF平行于BC，写出图中的所有等腰三角形
【试题答案】
一、1~5 B A B D D 6~
二、1、等边 2、5个 分别是：△AEF △ABC △EBD △FDC △DBC
3、底边的中垂线、3、4、无数 4、三条边 5、120°
三、1、答：AE=AC
解：∵AD是∠BAC的平分线
∴∠BAD=∠DAC
∵CE∥AD
∴∠BAD=∠E、∠ACE=∠DAC
∴∠E=∠ACE
∴AE=AC
2、答：△EDC是等腰三角形
理由：∵AB=AC ∴∠B=∠C， ∵ DE∥AB ∴∠B=∠EDC ∴∠EDC=∠C
∴ ED=EC
即：△EDC是等腰三角形
3、△EBO，△FCO